南水北调工程某标段GPS高程线性拟合改进方法研究
孟俊贞,马开锋, 黄桂平,赵继伟,杨卫森
(1. 华北水利水电大学 地球科学与工程学院,河南 郑州 450046;2. 华北水利水电大学 测绘与地理信息学院,河南 郑州 450046;3. 华北水利水电大学 水利学院,河南 郑州 450046)
0 引 言
GPS测量技术能够快速获取高精度的三维测量数据,是控制测量的首选方法. 但GPS测量结果只能给出相对于WGS-84椭球的大地高,不能直接应用于我国测绘生产与工程建设中所采用的正常高系统中,为此需要进行GPS高程的拟合转换. 近年来,许多学者进行了GPS高程拟合方面的研究[1-17],获得了丰富的理论与实践经验. 但当GPS控制网线形布设时,即可采用解析内插的方法进行确定待定点的正常高,即通过已知高程控制点的平面坐标与高程异常值,由构造的插值函数拟合测线方向上的似大地水准面曲线,然后内插其它点的高程异常值[8,12-13]. 比较经典的解析内插法主要有:多项式曲线拟合法、正交函数曲线拟合法、三次样条曲线拟合法与Akima曲线拟合法等. 每种方法各有特点、各具优势. 其中多项式曲线拟合法,虽然计算比较简单,但当存在较多拟合点采用最小二乘原理计算时,常常出现系数矩阵病态,使得拟合效果不理想. 故本文重点针对正交函数曲线拟合法、三次样条曲线拟合法与Akima曲线拟合法及其改进优化进行研究.
1 GPS高程线性拟合方法
1.1 正交函数曲线拟合法
GPS高程线性拟合方法中有常见的多项式拟合方法,但多项式拟合方法在用最小二乘法解算时,得到的系数矩阵常常是病态的,为了避免求解这种病态方程组,通常利用正交函数(函数向量内积为零的函数)来确定拟合多项式[13].
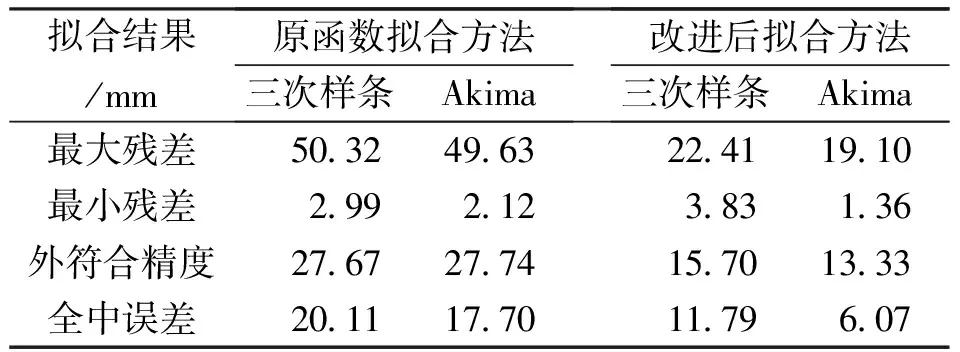
设给定n+1个数据点(xi,ξi)(i=0, 1, 2, …,n),需要确定一个m次的最小二乘拟合多项式(其中m (1) 式中,a0,a1,…,am为多项式系数. 若能够构造出一组次数不超过m的在给定点上的正交多项式Qj(x)(j=0,1,2,…,m),则可以首先用Qj(x)作为基函数,进行最小二乘拟合,即: Pm(x)=q0Q0(x)+q1Q1(x)+…+ qmQm(x), (2) 式中,系数qj(j=0,1,2,…,m)为 (3) 然后将各个qj代入式(2),并展开成一般多项式(1). 构造给定点上的正交多项式Qj(x)(j=0,1,2,…,m)的递推公式如下: (4) 其中: (5) (6) 其中: (7) 在实际计算中,可以根据递推公式(4)逐步求出各正交多项式Qj(x),并用公式(3)计算出组合系数qj. 同时,逐步将每次计算得到的qjQj(x)项展开后累加到拟合多项式(1)中,得到m次的拟合多项式. 将待求点的拟合坐标代入,即可求出其高程异常[13]. 在测线较长、己知点较多、高程异常变化较大时,按最小二乘原理求得的多项式系数削高补低的误差会增大. 为避免高次插值引起的振荡现象以及分段低次插值连接点上的不光滑性,通常采用以三次样条函数作为拟合模型的分段计算方式. 三次样条曲线实际上是由多段三次多项式曲线拼接而成的连续曲线.在段间连接点处,不仅函数自身连续,且其一阶导数和二阶导数也是连续的.这样不仅克服了单个多项式不灵活、不稳定的缺点,而且保留了多项式的表达与计算的简便性,因而在较长测线GPS高程拟合中得到了较为广泛的应用. ξ(x)=ξ(xi)+(x-xi)ξ(xi,xi+1)+ (x-xi)(x-xi+1)ξ(x,xi,xi+1), (8) ξ″(xi)(i=1,2,…,n-1)满足系数矩阵为对称三角阵的线性方程组: (9) 用追赶法求解方程组(9),可求出ξ″(xi),而 ξ″(x)=ξ″(xi)+(x-xi)ξ″(xi,xi+1). (10) 利用二阶差商与式(10),可求得ξ(x,xi,xi+1),再将ξ(x,xi,xi+1)代入式(8),即可求得待定点的高程异常拟合值. 该方法是指在两个已知点间内插时,除用这两个己知点外,还需用两己知点外的两个点,其目的是使函数曲线光滑、连续. 设有6个已知点(i=1, 2, …, 6),现需要在3号点和4号点之间内插任一待求点,其计算公式为 ξ(x)=P0+P1(x-x3)+P2(x-x3)2+ P3(x-x3)3. (11) 式中: (12) 式(12)中的t3、t4为3号点和4号点实测要素的斜率,t3用1~5号已知点计算,t4用2~6号已知点计算,一般计算公式为 (13) 式中,mi=(ξi+1-ξi)/(xi+1-xi). 当式(13)中分母为零时,ti=1/2(mi-1-mi)或ti=mi. 在进行上述正交函数、三次样条、Akima等曲线拟合过程中,由于用于曲线拟合的已知点与检核点不可能严格分布在一条直线上,故根据已知点与基准点之间的距离来求某一点的拟合坐标,显然是不够准确的,为了改善曲线拟合的精度,在已有曲线拟合方法的基础上,进行了曲线拟合坐标算法的改进优化. 假定曲线上第一个已知点的拟合坐标为0,则其中一个点的拟合坐标xi为该点与前一点的距离ri,i-1再加上前一点的拟合坐标xi-1,公式可表示为 xi=xi-1+ri,i-1. (14) 为了客观评定GPS高程拟合计算的精度,通常在布设几何水准联测点时,在其施测区域内适当多联测几个GPS点,作外部检核用. 所以,在评定GPS水准拟合精度时,一般主要采用外符合精度与每千米水准测量全中误差两个评价指标. (15) 2)每千米水准测量全中误差Mw各相邻检核点高差较差DVh可看作是符合水准路线的闭合差,如此可计算出每千米水准测量全中误差Mw,具体计算公式如下: (16) 式中:N为高差个数;F为比较高差的检核点间距离,km. 南水北调工程某标段已测量的GPS点位数据和四等水准数据结果,如表1所示. 其点位位置分布如图1所示. 表1 已测数据结果 图1 点位分布图 由图1可知,该区域所测点位呈线性分布,故较适合于采用GPS线性拟合方法进行高程异常拟合. 为验证文中所提改进方法的有效性,分别采用正交函数、三次样条与Akima曲线模型对其进行高程拟合,并采用外符合精度M与全中误差Mw进行拟合精度比较分析. 方案一:对正交函数(此处采用三阶函数)与三次样条曲线拟合进行验证,此处选取A1、A4、A6、A7、A8、A9、A12、A14这8个点来计算拟合模型参数,其余点作为检核点进行拟合残差计算及精度结果评定,如表2所示. 方案二:对三次样条与Akima曲线拟合进行验证,此处选取A1、A2、A3、A5、A7、A9、A12、A13、A14这9个点来计算拟合模型参数,其余点作为检核点进行拟合残差计算及精度结果评定,如表3所示. 表2 方案一拟合结果 表3 方案二拟合结果 表2结果表明,采用原正交函数与三次样条曲线拟合方法时,针对此选点方案原正交函数与三次样条曲线拟合方法得到的结果,其全中误差分别达到了8.88 mm与14.44 mm,很明显正交函数曲线拟合方法的精度结果较好. 而通过两者改进后的方法分别进行拟合计算可知,改进后的正交函数与三次样条曲线拟合方法拟合结果精度的全中误差均有提升;但改进后的正交函数拟合结果中,其最大残差与外符合精度还有所变大,这是由于计算其模型参数时所选点位的非线性组合方案导致的;而改进后的三次样条曲线拟合结果的精度有明显改善,其精度提高了一倍,全中误差达到了7.00 mm,从而显示了改进后三次样条曲线拟合方法针对此选点方案的优越性. 表3结果表明,采用原三次样条与Akima曲线拟合方法时,针对此选点方案三次样条与Akima曲线拟合方法得到的结果,其全中误差分别达到了20.11 mm与17.70 mm,相对来说Akima曲线拟合方法的精度结果较好. 而通过两者改进后的方法分别进行拟合计算可知,改进后的三次样条与Akima曲线拟合方法拟合结果精度均有明显提升,其中改进后的三次样条曲线拟合结果的精度提高了近一倍,全中误差达到了11.79 mm,改进后的Akima曲线拟合方法拟合结果的精度提高了近两倍,全中误差达到了6.07 mm,从而显示出了改进后的Akima曲线拟合方法针对此选点方案的明显优越性. 通过总体分析,在选点适宜的情况下,采用改进后的Akima曲线拟合方法能够对线性区域的GPS高程异常进行较高精度的拟合计算,可以作为GPS高程线性拟合的首选方法. 本文方法主要针对相对较为线性的区域进行了数据测试验证,若拟合区域存在较大弧段时,本文方法是否有效,还需进一步测试研究. 通过分别采用原正交函数、三次样条与Akima曲线拟合方法与分别改进后的拟合方法对南水北调工程某标段的GPS高程线性拟合,得到了针对不同的选点方案,同一种拟合方法也有不同的拟合精度结果;针对同一种选点方案,不同的拟合方法也有不同的拟合精度结果;而对于文中所提的改进后的曲线拟合方法均有不同程度的精度提升,其中改进后的Akima曲线拟合方法的拟合精度结果提升最为明显,故针对线性拟合区域在选点适宜的情况下,可以考虑采用改进后的Akima曲线拟合方法对其GPS高程异常进行较高精度的拟合计算,从而获得较理想的高精度拟合结果.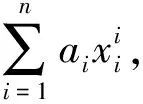
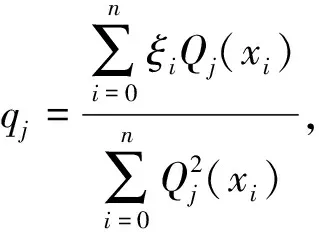
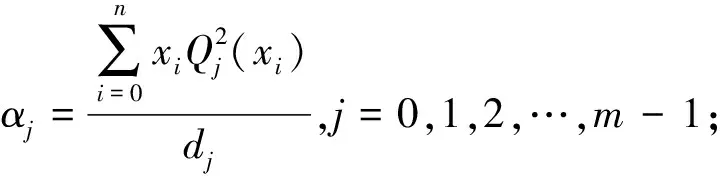

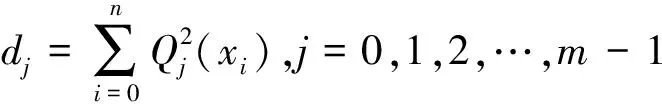
1.2 三次样条曲线拟合法
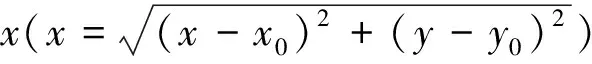
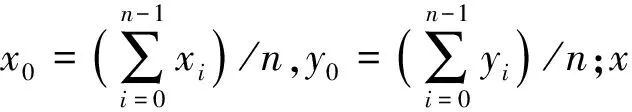
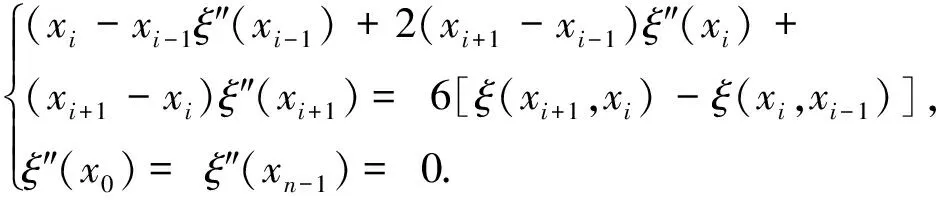
1.3 Akima曲线拟合法
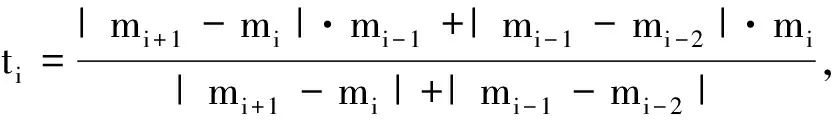
2 GPS高程线性拟合改进方法及精度评定
2.1 GPS高程线性拟合改进方法
2.2 精度评定

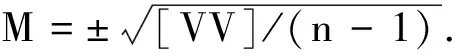
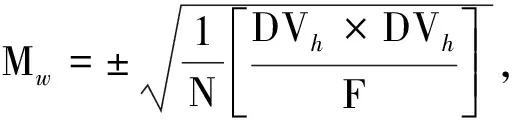
3 实例应用
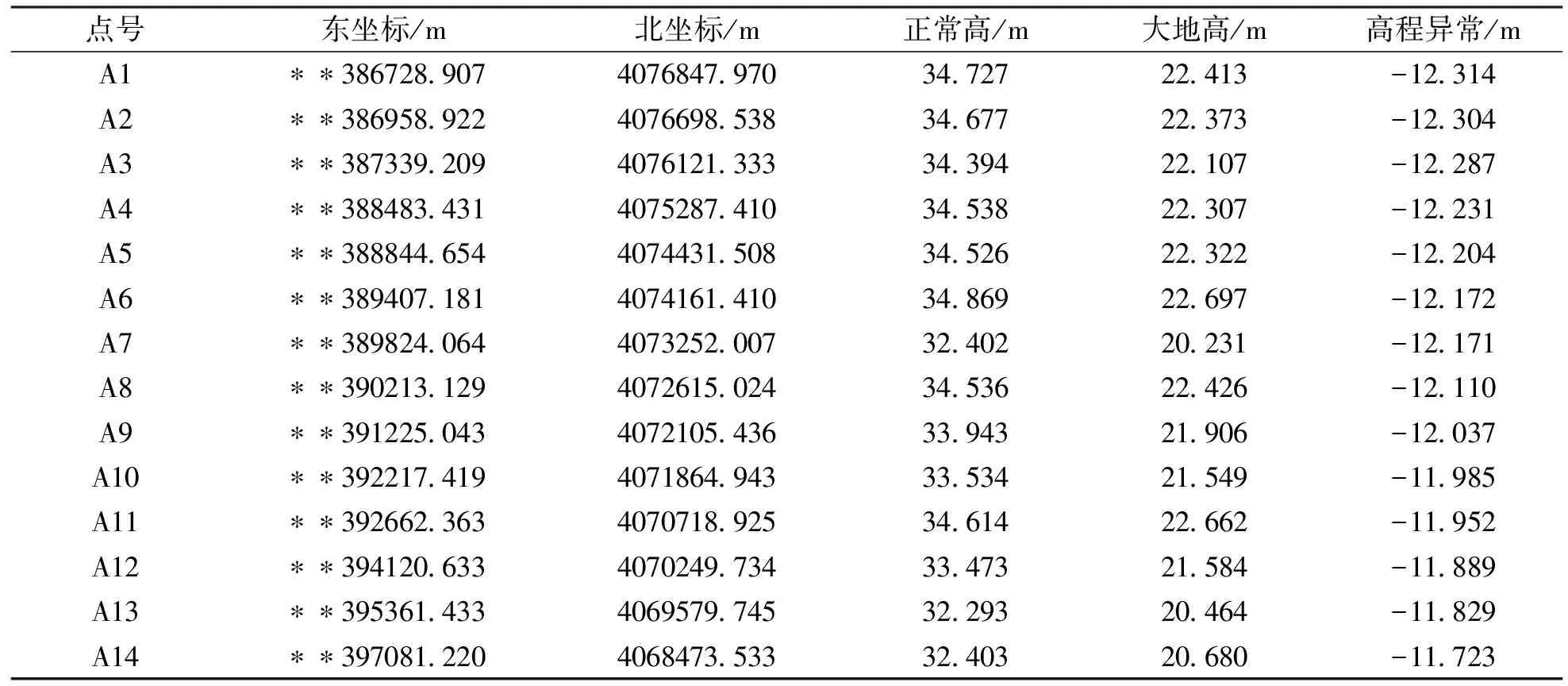
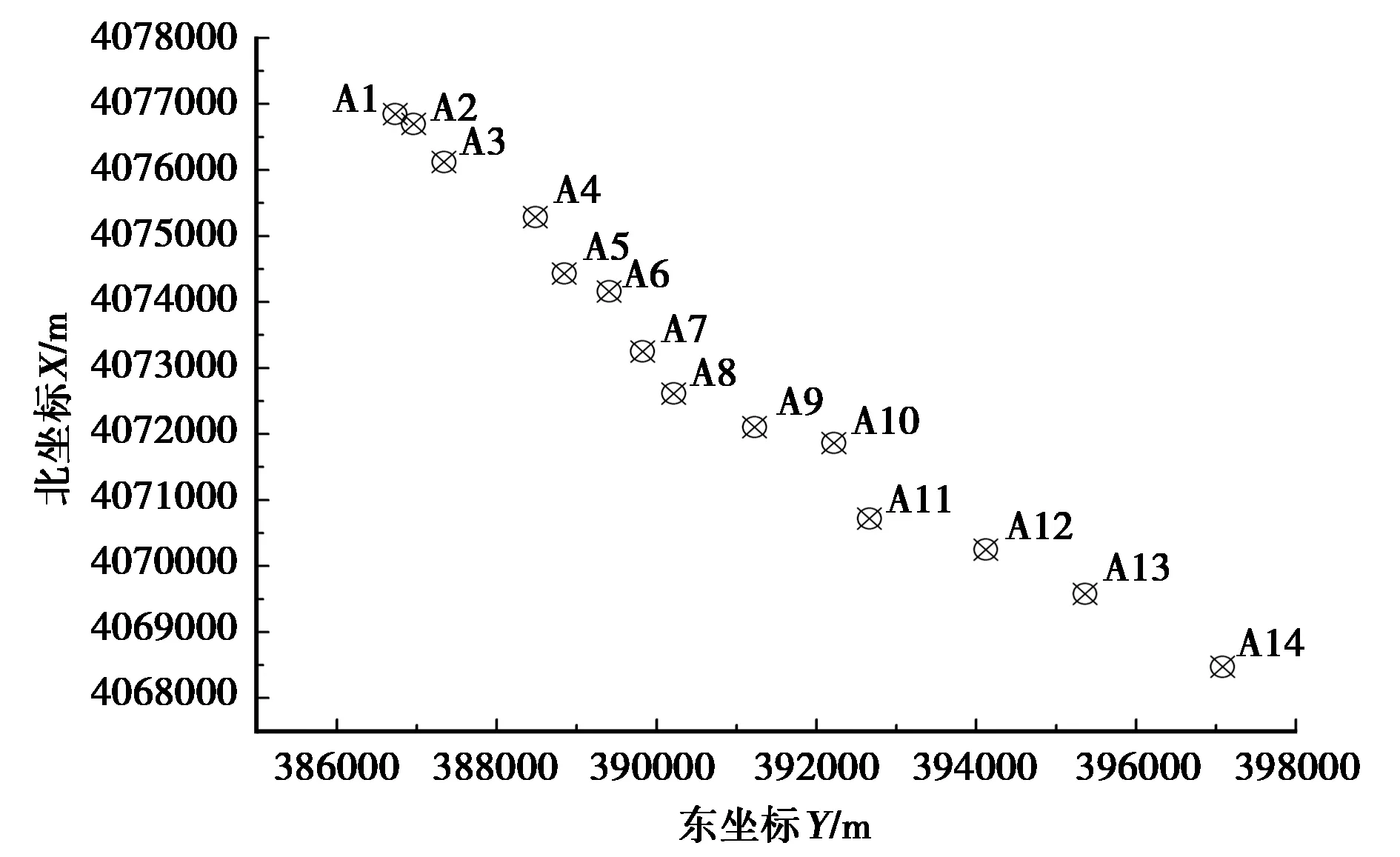

4 结束语

