小波和傅里叶变换在坐标时间序列分析中的应用

蔡富，孙付平，戴海亮，朱新慧，张龙龙

(信息工程大学 地理空间信息学院, 河南 郑州 450001)

0 引 言

由于各种地球物理效应,大部分GPS坐标时间序列存在明显的非线性变化,尤以垂直方向最为明显[1]．如何有效地提取非线性变化中的有用信息是在进行坐标时间序列分析时经常遇到的问题．传统的谐波分析方法是建立在傅里叶变换的基础上的,傅里叶变换具有较好的频域分辨率,能够精确地确定时间序列中各次谐波的频率和振幅．但是傅里叶变换反映的是信号总体在整个时间段的频域特征,当将时间序列从时域变换到频域时,其在时间域上的信息就丢失了,因此不能很好地反映时间序列的细节特征．而且基于傅里叶变换的时间序列分析方法一般是建立在信号平稳的假设基础之上,而绝大部分的时间序列其整体趋势是不平稳的[2]．故而傅里叶变换具有一定的局限性．而小波变换则可以改变这种局限性,研究表明,小波变换可以对许多含有周期性规律的时间序列进行时频分析,在地球物理等领域应用广泛[3-5]．利用多尺度分析的原理,小波变换可以将时间序列分解到不同尺度上进行研究,并能进行不失真重构,能够得到时间序列的细节信息,因此对处理非平稳时间序列优势明显[6-7]．但是通过小波变换得到的只是各次谐波的时域波形,还不能很精确地得到时间序列的频率和振幅信息．而且实验表明,当所处理的时间序列中含有较长周期项时,仅基于小波变换这一单一技术很难对其进行准确确定．目前，综合傅里叶变换和小波分析的研究现状来看,单一的研究途径和方法不再适合于复杂的时间序列分析与预测,而多种理论和方法的有机结合能为正确分析和解决问题提供有效途径．

本文综合考虑小波变换时频局部分析优势和傅里叶变换频域分析优势,提出一种小波变换与傅里叶变换相结合的方法来对坐标时间序列进行分析．

1 基本理论

1.1 傅里叶变换

傅里叶变换能够将信号在时域和频域中相互转化, 其实质是把时域中的原始信号f(t)分离为多种不同周期(频率)的正、余弦波之和,进而对时间序列进行分析．这种变换是可逆的且能量保持不变[8]．定义如下式:

(1)

其反变换为

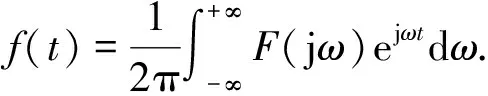
(2)

式中：f(t)是时间域的信号；F(jω)是快速傅里叶变换的结果,为函数f(t)的频谱密度函数,f(t)为F(jω)的原函数[9]．根据定义可知,原始信号f(t)在经过傅里叶变换后其时间域的信息就消失了,即F(jω)只有频率特性,且其值由f(t)在整个时段的特性所决定,利用傅里叶变换这一特性可获取信号所有频率．

通过傅里叶变换,在时域中连续变化的信号可转化为频域中的信号,因此傅里叶变换反映的是整个信号在全部时间下的整体频域特征,但不能反映信号的局部特征．

1.2 小波变换

小波变换是一种时间-频率分析方法,与傅里叶变换相比,在分析非平稳时间序列方面优势明显,因此成为当前分析时间序列的有效工具．小波变换的定义如下[10]:

设f(t)是一平方可积函数,记作f(t)∈L2(R),ψ(t)为母小波,如果ψ(t)满足容许条件:

(3)

则有下式:

(4)

式(4)为函数f(t)的小波变换,式中：a为尺度因子；b为位移因子．

另外,小波变换也可以写成式(5)所示的卷积形式:

(5)

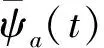
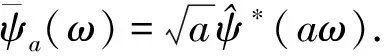
(6)

1.3 小波变换的多分辨率分析

1988 年Mallat提出的多分辨率分析(MRA)是小波分析的重要概念,又称为多尺度分析．小波变换的MRA能将时间序列在不同分辨率上进行分解,分别得到低频部分和高频部分,其中低频部分能够反映时间序列的概貌,而高频部分又叫细节部分,能够刻画时间序列的细节信息,因而将小波变换誉为“数学显微镜”[11-13]．小波变换的这种多尺度分解能力可以将各种频率叠加在一起的信号分解为不同频率的子信号,使得一种分辨率下无法发现的特性在另一个分辨率下很容易被发现,从而能够有效地应用于信号和噪声分离、信号的分析与重构、特征提取等问题[14-15]．

小波多分辨率分析主要是通过空间分解,将信号分解在子空间列中,方便进行信号分析[16]．小波多分辨率分解示意图如图1所示,其中S表示原始时间序列,A1、A2、A3表示小波分解后各层时间序列的低频部分,D1、D2、D3则表示小波分解后各层时间序列的高频部分．小波变换能将信号不断分解成低频和高频两部分,进而由粗到细地逐步观察时间序列,具有多尺度分析的特点．此外,各部分与原始信号具有以下关系:S=A3+D3+D2+D1.以此类推,若要进行进一步的分解,则可以把低频部分A3作为高频部分D4和低频部分A4的叠加．可以将小波分析视为近似无损的信号处理方法．

图1 小波多分辨率分解示意图

大多数情况下,由于受到不同地球物理因素的影响,测站时间序列表现出来的随机性较强,异常变化在部分时段内时有发生．频谱分析虽然能够分析出时间序列中有色噪声的频率特征,并从频域发现时间序列的周期性趋势项,但是却不能有效探测异常区间．通过小波分析,就能够根据小波多尺度分析的原理对分解后的各层时间序列进行分析,确定异常区间,从而达到提取测站时间序列特征信息的目的[16]．

2 小波和傅里叶变换相结合的方法及分析

2.1 数据描述

实验数据来源于国际地球参考框架ITRF2008的GPS坐标残差时间序列数据,可在官网(http://itrf.ensg.ign.fr/ITRF-solutions/2008/)上下载,而且残差时间序列已经剔除了固体潮、极潮等部分环境负荷的影响[17-18]．由于GPS 测站遍布全球,各站地理环境不同导致坐标时间序列数据质量不一,时间序列所表现的特征信息如周期规律等也就存在差异,有的测站还存在时间间隔较长的间断点和突变信息．为了使结论更具有普遍性,本文分别从低、中、高纬度各选取了3～4个测站进行了实验分析, 所选的测站信息如表1所示．

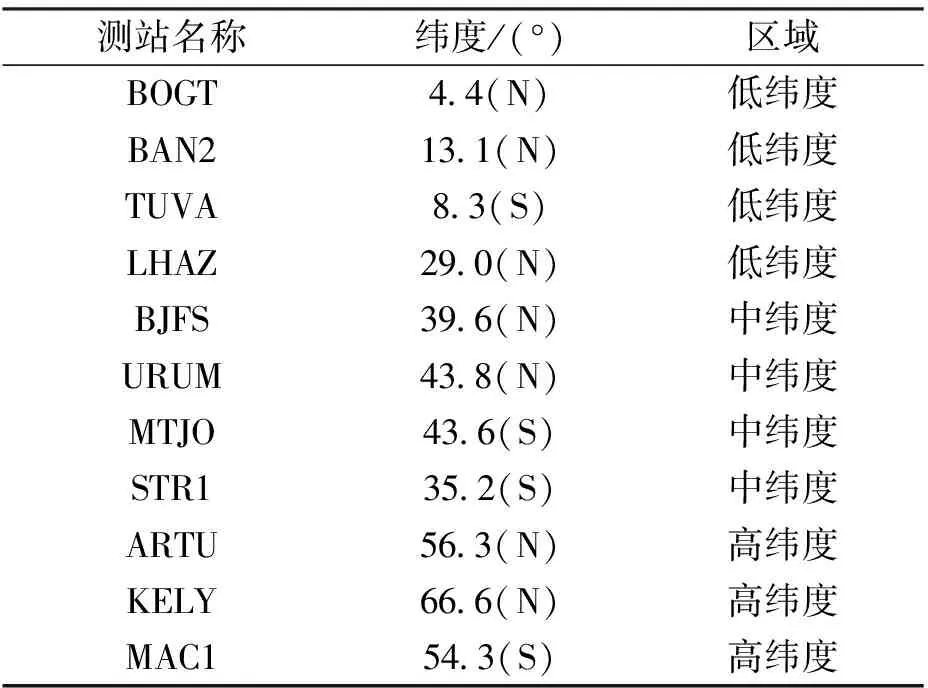
表1 GPS测站位置

2.2 小波基函数的选取

选取不同的小波基函数,小波变换的结果也不同．目前广泛使用的小波基函数有haar小波、dbN小波、symN小波、coif小波、bior小波、rbio小波等,不同的小波基函数有不同的对称性、消失矩和正则性等性能特点,在波形上也表现出了很大的差别[19]．本文在对坐标时间序列数据进行大量的实验分析表明选用dbN小波效果较好．dbN小波作为稀疏基所引入的光滑误差很难被探测,因此信号重构过程比较光滑．伴随着阶次的增大,消失矩阶数亦随之增大,光滑性变得越好,频域的局部化能力就越强,划分频带效果越好,但时域紧支撑性减弱,同时计算量剧增,实效性变差[20]．另外,dbN小波没有明确的表达式,除N=1外(N=1时即为Haar小波)．

2.3 随机项的提取

去除长期趋势项后,坐标时间序列中的其它层就是随机项和周期项,而且在地球物理现象和经济领域等实际问题中,随机因素往往是小尺度成分,因此,在大多数情况下,第一次小波分解的高频部分中包含的随机项的成分最多,其它层中包含的周期项成分较多[21]．如图2所示的URUM站垂向坐标时间序列中,既有周期性规律，还存在着一些随机变动,使用具有正交性和高度紧支撑性的db4小波,分解5层分别得到a1～a5的低频部分和d1～d5的高频部分,随机变动信息通常包含在每一层的高频部分中．如图3所示,可以发现,高频部分d1、d2中存在着一些随机变动信息,即随机项,而且由d1可以看出在URUM站垂向坐标时间序列在第475周附近存在跳变,量值达到8 mm．表明了小波变换对细节信息的把控能力比较强．

在对坐标时间序列进行小波多尺度分解后,对于包含随机项的各层,其在不同尺度上的成分一般相互独立,而且经常是平稳的,因此可以分别进行处理．

图2 URUM站垂向坐标时间序列

图3 小波分解后的各层低频和高频部分

2.4 周期项的提取

小波分析是一种时、频MRA方法,它可以对函数和信号系列进行多尺度细化分析,以分析不同尺度(周期)随时间的演变情况．小波分析能将时间序列的频率特征在时域上显现出来,分析其主周期项,而且能准确地给出变化趋势和突变点以及各时间尺度(周期)的长短和分布情况．将待分析时间序列通过合适的小波基函数和分解层次分解成低频部分和高频部分,并投射到相应尺度上．对剩余细节信号采用傅里叶变换进行周期分析,实现周期性信号的探测．如果有些层的周期性还不十分明朗,可对该层再进行小波分解,直到能够方便地分析该层的波形为止．

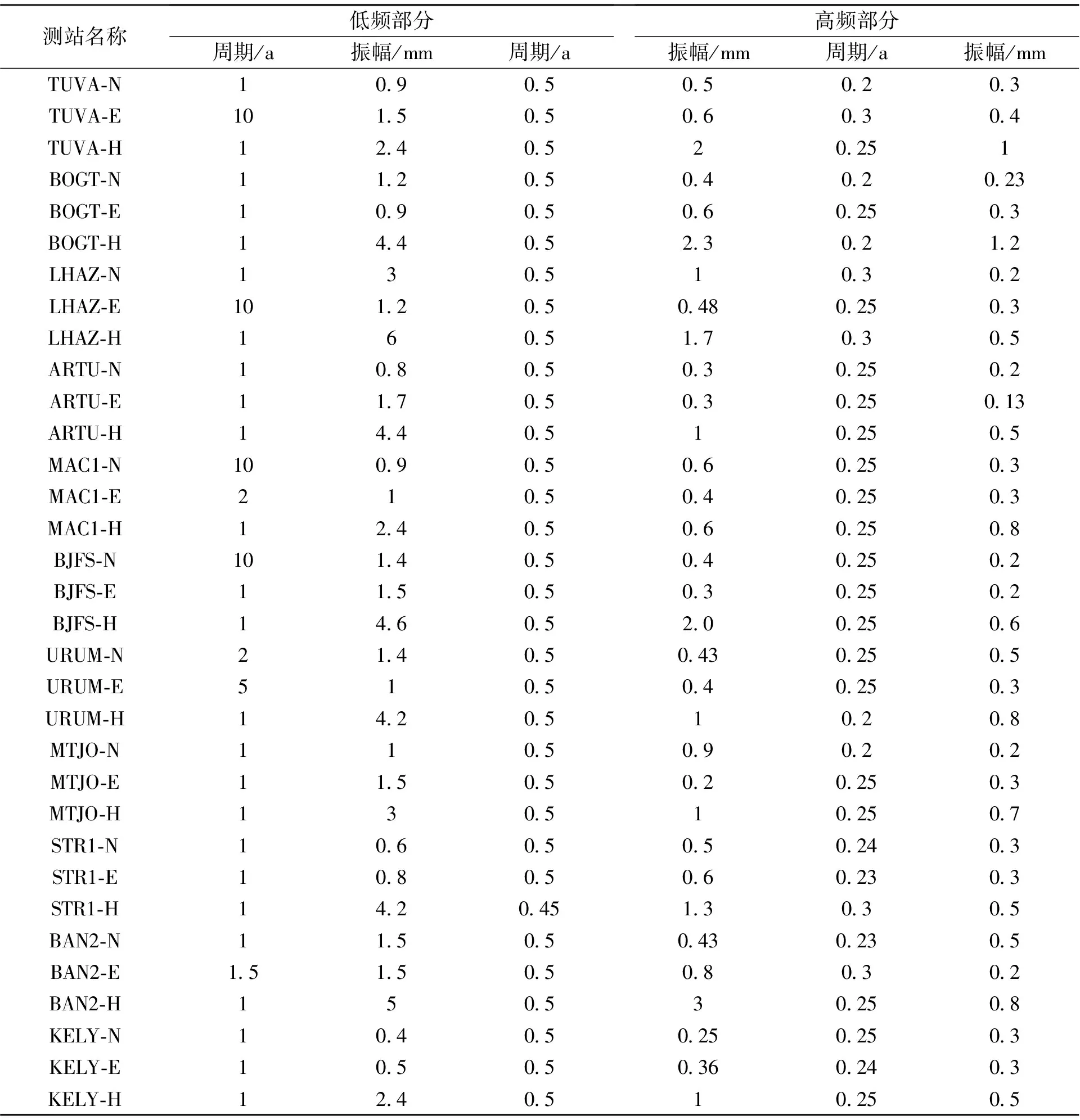
如图3所示,由低频部分a3和a4可以看出URUM站垂向坐标时间序列中存在1年周期项,并且为其主周期项,由d4可以看出半年周期项,由a5第0～100周时间段可以看出时间序列中存在2年周期项．这与快速傅里叶变换的结果也是相吻合的．虽然小波变换存在诸多优势,但分析发现很难确定主要周期项的振幅,而且对于一些测站存在长周期如10年、12年,以及短周期项如季节周期项、月周期项的情况,小波变换优势并不明显．因此,在小波变换的基础上,对分解得到的高频或低频信息进行傅里叶变换,提取其周期项及相应的振幅信息．如图4在对BJFS站N方向上坐标时间序列进行小波分解时,虽然能根据高频部分d5看出周期为1年的周期项,但是其他周期项则不明显．鉴于快速傅里叶变换频率特性较好,这里对低频部分a5进行傅里叶变换,可以得到周期为10年,振幅为1.44 mm的周期项,以及周期为3年,振幅为1.39 mm的周期,如图5所示．对d5进行快速傅里叶变换可以确定其1年周期项的振幅为0.80 mm．以此类推,将BJFS站N方向小波分解得到的各层主要周期项及振幅进行统计结果如表2所示,“周期/a”中a指周年．

表2 小波分解得到的各层主要周期及振幅

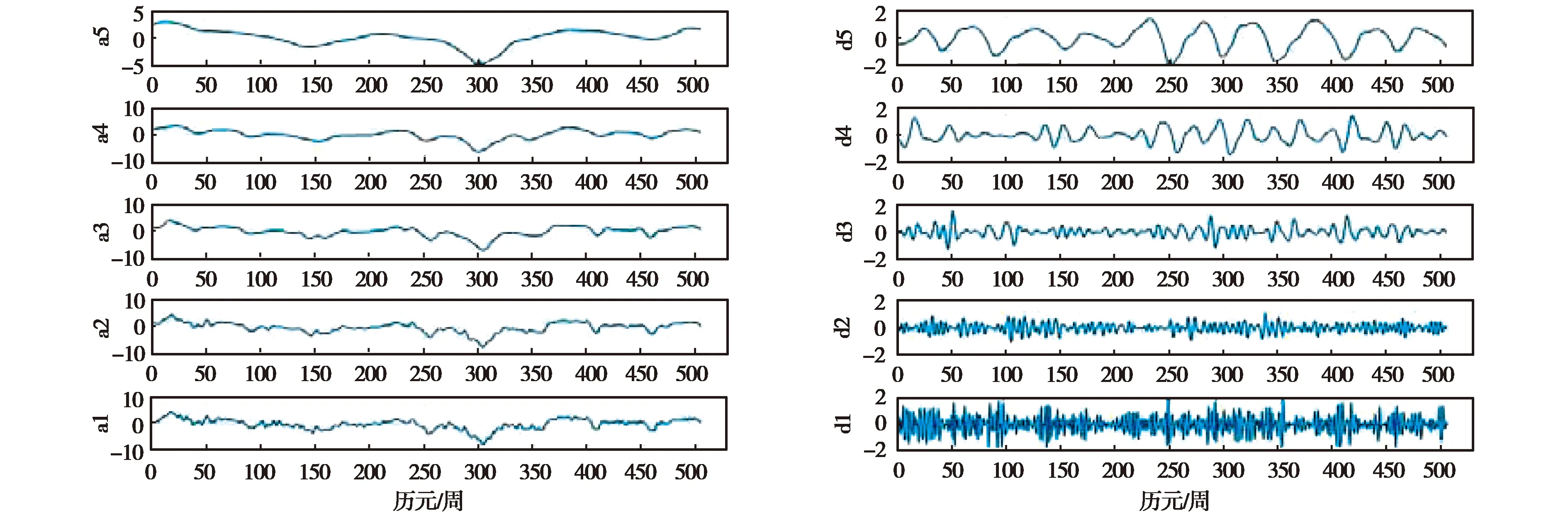
图4 BJFS站N方向小波分解后的各层低频和高频部分

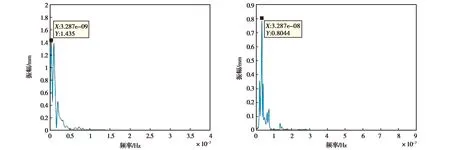
图5 小波第5次分解得到的低频和高频分量频谱图

测站名称低频部分周期/a振幅/mm周期/a高频部分振幅/mm周期/a振幅/mm TUVA-N10.90.50.50.20.3 TUVA-E101.50.50.60.30.4 TUVA-H12.40.520.251 BOGT-N11.20.50.40.20.23 BOGT-E10.90.50.60.250.3 BOGT-H14.40.52.30.21.2 LHAZ-N130.510.30.2 LHAZ-E101.20.50.480.250.3 LHAZ-H160.51.70.30.5 ARTU-N10.80.50.30.250.2 ARTU-E11.70.50.30.250.13 ARTU-H14.40.510.250.5 MAC1-N100.90.50.60.250.3 MAC1-E210.50.40.250.3 MAC1-H12.40.50.60.250.8 BJFS-N101.40.50.40.250.2 BJFS-E11.50.50.30.250.2 BJFS-H14.60.52.00.250.6 URUM-N21.40.50.430.250.5 URUM-E510.50.40.250.3 URUM-H14.20.510.20.8 MTJO-N110.50.90.20.2 MTJO-E11.50.50.20.250.3 MTJO-H130.510.250.7 STR1-N10.60.50.50.240.3 STR1-E10.80.50.60.230.3 STR1-H14.20.451.30.30.5 BAN2-N11.50.50.430.230.5 BAN2-E1.51.50.50.80.30.2 BAN2-H150.530.250.8 KELY-N10.40.50.250.250.3 KELY-E10.50.50.360.240.3 KELY-H12.40.510.250.5

采用上述数据处理流程和方法,本文对所选测站进行了处理分析,鉴于篇幅,只对小波分解后的各层主要周期项及振幅变化进行了统计,结果如表3所示．

综合上述实验分析,高低频小波MRA对坐标时间序列周期项的提取各有优缺点．低频分析可以较容易地得到“周年项”和 “两年周期项”,但较长周期项(2年以上周期项)和短周期项(1年以下周期项)则不易发现,可以结合傅里叶变换进一步求取;高频分析能够较准确提取“半周年项”、“一季项”等短周期．基于小波变换和傅里叶变换相结合的综合分析方法，可以对小波分解的每层信号进行分析,能够结合两者的优势,达到提取坐标时间序列中特征信息的目的．

3 结 论

本文依据GPS测站残差时间序列非线性变化的特点以及小波变换和傅里叶变换在坐标时间序列分析中各自的优势,提出了一种小波分析和傅里叶变换相结合的时频分析方法,来提取坐标时间序列中的特征信息,得到了以下结论:

1)利用傅里叶变换可以得到时间序列中各次谐波的频率和振幅,但当将时间序列从时域变换到频域时,容易丢失其在时间域上的信息,不能很好地反映时间序列的一些细节特征,如间断点和突变信息等,因此具有一定的局限性．

2)小波MRA可以将坐标时间序列分解到不同尺度上,得到时间序列的细节特征和一些周期信息,在处理非平稳时间序列时优势明显．其中低频分析可以直观地得到“周年项”和 “两年周期项”,但2年以上的长周期项和1年以下的短周期项则不容易发现;而高频分析能够较准确提取“半周年项”、“一季项”等短周期．但是通过小波变换得到的只是各次谐波的时域波形,还不能很精确地得到时间序列的频率和振幅信息．

3)与单一采用小波变换或傅里叶变换相比,小波和傅里叶变换相结合的方法既能保留测站坐标时间序列的时间信息,又能在不同尺度上对时间序列进行分析,解决了小波变换部分周期项难提取和傅里叶变换时间信息容易丢失的问题,非常适用于对复杂的时间序列进行分析和研究．而且,这种方法在一定程度上也克服了小波基函数的选取问题,因此具有较高的研究价值.