PPP技术在无基准或多基准测区应用研究

冯江海,刘少英,郝恒强,王凯

(1.解放军 63869部队,吉林 白城 137001;2.兰州天地测绘有限公司,甘肃 兰州 710020;3.北京特种工程设计研究院,北京 100028)

0 引 言

在常规武器试验过程中,往往需要建立发射阵地和落区之间统一的测量基准,根据“首级控制逐级加密”的布网原则,我们通常在阵地或者落区选择较近的控制网点坐标成果作为首级控制网起算点,然后为了统一测量基准,进行阵地和落区的控制网联测,这在射程较短时是切实可行的,但在远射程试验中却由于测量周期过长、累计误差过大而导致实施难度增大．如果阵地和落区附近均有控制网点,有时也可以独自建立测量控制网,但由于引入的控制网点形成的坐标框架和测量历元不统一而导致阵地和落区坐标基准不同,在陌生地域进行武器试验时,往往缺乏可用的已知点,只能进行远距离控制点坐标传递,严重影响了点位测量精度和试验进度．本文通过分析精密单点定位(PPP)解算精度,对PPP技术用于无基准区域或者多基准区域首级控制网建立的可行性进行了分析,同时分析了不同测量成果之间的框架误差和历元误差,得出了相关可靠的结论．

1 PPP基本原理

PPP是利用GPS非差载波相位观测值和IGS等组织提供的精密轨道和钟差产品,采用严密的绝对定位模型,处理单台接收机采集的双频数据,从而得到国际地球参考框架(ITRF)坐标基准下厘米级测站坐标的一种单点定位方法．式(1)为PPP的观测方程[1]:

L0=ρ+c(dt-dT)+λN+M·z+ε,

(1)

式中：L0为L1和L2无电离层相位组合观测值;ρ为测站与卫星间的几何距离;dt为接收机钟差;dT为卫星钟差;N为无电离层组合相位观测值的模糊度;M为投影函数;z为天顶方向的对流层延迟改正参数;ε为组合相位观测值的观测噪声和多路径误差．

由于具有单台作业无需同步观测、解算精度均匀无累积误差,可直接得到ITRF框架下三维地心坐标等特点,在工程应用中得到广泛的使用．

2 GrafNav/Net介绍

GrafNav/Net是加拿大WayPoint公司开发的GPS/GLONASS事后处理软件包,主要包括GrafNav、GrafNet、GrafNav Batch和Utilities四个模块,可有效处理GPS单频、双频和GLONASS系统的测量数据．软件版本8.1以后新增了PPP处理功能,其中静态测量和动态测量可达到如表1、表2所示的定位精度[2]．

表1 静态测量定位精度

表2 动态测量定位精度

3 PPP用于无基准区域首级控制网布设的可行性分析

3.1 误差源分析

PPP的误差源可分为与卫星有关的误差、与信号传播有关的误差以及与地面接收机有关的误差三项[3]：

1)与卫星有关的误差包括卫星钟差、卫星轨道误差、天线相位中心偏差、相对论效应误差等．PPP中通常采用精密卫星钟差文件(标称精度可达到0.1～0.2 ns)、精密卫星星历文件(事后精密星历的精度大约为2～5 cm),并采用PCO/PCV差值算法进行卫星天线相位中心改正,从而有效降低与卫星有关的相关误差．

2)与信号传播有关的误差包括电离层延迟、对流层延迟、多路径效应误差等．针对电离层延迟误差,PPP中常利用双频观测值组合消除一阶项,此时剩余的高阶项影响小于3 cm[4-5],对于对流层延迟误差影响,通常采用模型进行修正,此时干分量部分改正精度可以达到厘米级[6],然后对湿分量部分的残余影响进行参数估计．针对多路径效应影响,采用抑制天线、相控列阵天线的同时采用半参数估计、小波分析等方法．

3)与接收机有关的误差包括接收机钟差、接收机天线相位偏差、固体潮改正、海潮改正、地球自转改正等．对于接收机误差通常将其与观测站的未知参数一并求解,而对于其它几项改正通常采用相应的改正模型进行求解．

3.2 算例分析

算例一:选取全球范围内的22个IGS站在历元2018.339当天24 h的观测值数据和导航电文,利用GrafNav进行PPP解算,并与IGS发布的逐日解坐标进行对比,经坐标形式变换后可得到高斯投影平面和高程的轴系残差,如图1所示．选取IGS站BJFS、DAEJ从2017年9月1日至2018年8月30日每月1日、15日的观测数据,分别进行PPP数据解算,并与IGS发布的逐日解坐标进行对比,得到轴系残差如图2、图3所示．

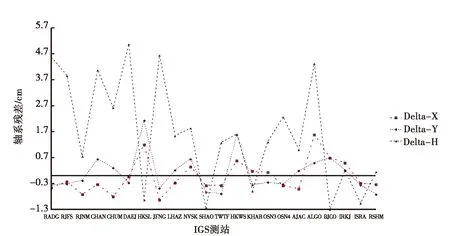
图1 同一历元不同IGS站PPP数据对比

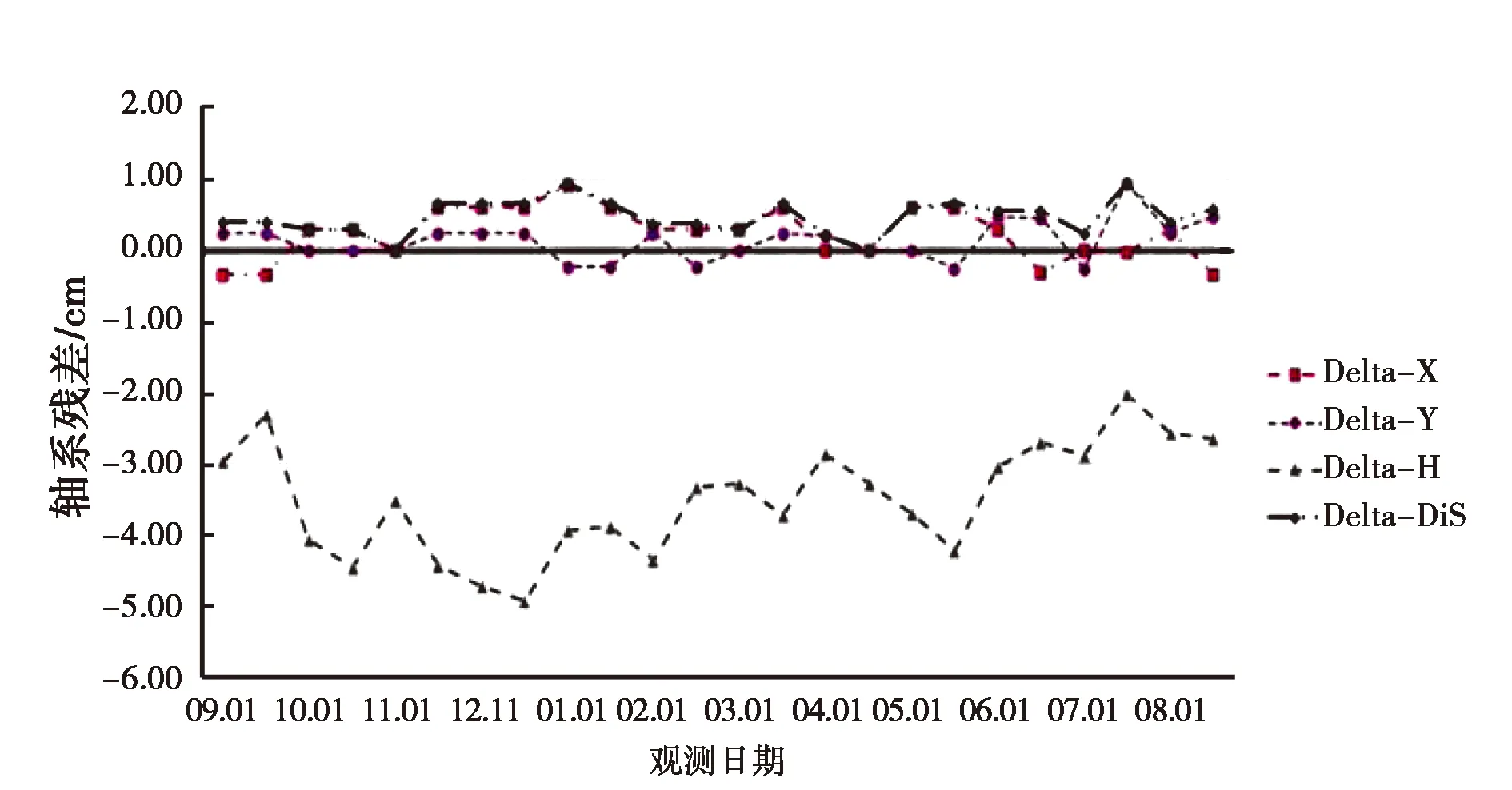
图2 BJFS站PPP解算各轴系误差

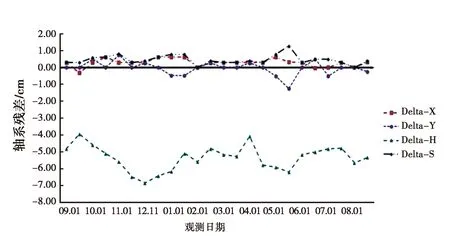
图3 DAEJ站PPP解算各轴系误差

从图1可以发现利用GrafNav进行PPP求解,可以达到厘米级解算精度,从图2、图3可以发现BJFS站、DAEJ站在一年内PPP解算精度比较稳定,平面平均误差小于1 cm,高程平均误差小于10 cm．此时理论上只存在星历误差、较小的观测误差、PPP算法误差以及高斯投影变形等误差项的影响．

算例二:利用TEQC数据预处理软件将BJFS站EPH2018.054当天24 h的数据从1～10 h步长0.5 h进行分割,分别进行PPP求解,并与IGS发布的逐日解进行对比,可得轴系误差变化图如图4所示．同时将该天的数据按要求分别选取连续的12份2 h、4 h、8 h观测值数据,分别进行PPP求解,可得平面精度稳定性和高程精度稳定性如图5、图6所示．

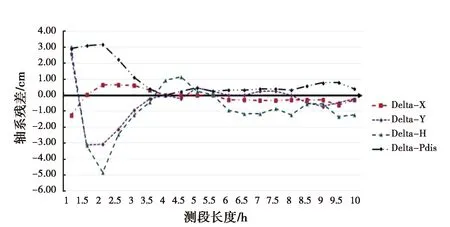
图4 BJFS站不同测段PPP解算各轴系误差

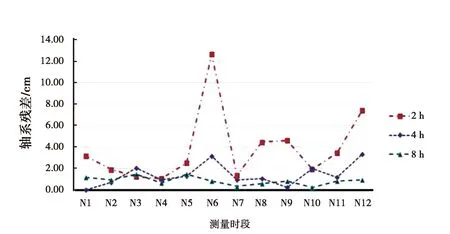
图5 BJFS站不同测段PPP平面精度稳定性

图6 BJFS站不同测段PPP高程精度稳定性

如图4所示,平面解算精度比高程解算精度高,当测段超过4 h,随着测段的延长,轴系误差较小,基本上小于2 cm;通过分析图5、图6可以发现,测段时间越长,PPP解算精度的稳定性越好,实际工程应用中可根据需要选取相应的测段长度．

4 PPP用于多基准区域首级控制网布设可行性分析

当阵地和落区存在不同的测量基准时,为了统一基准,通常进行阵地和落区控制网联测或者坐标基准变换(包括框架转换和历元变换),控制网联测往往导致完成周期很长且误差累积很大,影响任务完成进度．而进行坐标基准变换时需要用到测站的速度场信息,一般利用NNR-NUVEL-1A模型进行解算[7]或利用若干基准点进行线性内插[8],导致转换坐标存在较大的转换误差,且有的测量成果由于形成时间较早,参考框架和参考历元不可知,无法进行框架历元变换,此时利用PPP建立统一基准的首级控制网,在精度满足的前提下将会有更大的可行性．

4.1 ITRF框架历元变换原理

ITRF是目前国际上公认的精度最高、稳定性最好的参考框架,迄今为止国际地球自转服务(IERS)已经发布了ITRF88、ITRF89、ITRF90、ITRF91、ITRF92、ITRF93、ITRF94、ITRF96、ITRF97、ITRF2000、ITRF2005、ITRF2008共12个版本以及即将全面使用的ITRF2014．不同的ITRF间可采用14个转换参数(即7个转换参数和7个转换参数的速率[9])利用坐标系之间的相似变换进行转换,即:

(1)

(2)

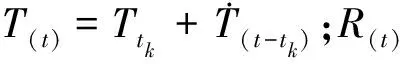
进行ITRF框架坐标转换一般有两种思路:一种是先统一历元再进行框架转换,另一种是先进行框架转换再统一历元,理论上两种方法可以得到的结果是一致的[10]．

4.2 算例分析

算例三:用ITRF2008框架下BJFS(EPH 2018.621)、LQC-XN(EPH 2018.704)的坐标,先进行历元变换(先将历元统一归算到2000.000历元),然后进行框架变换,并与ITRF2008框架相同历元下的坐标进行对比,可得轴系差异如图7、图8所示．

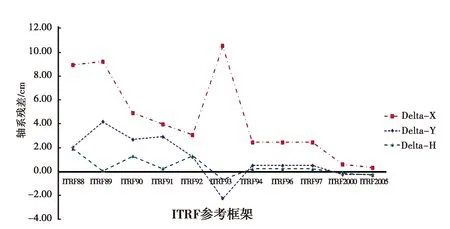
图7 BJFS站不同ITRF坐标框架差异

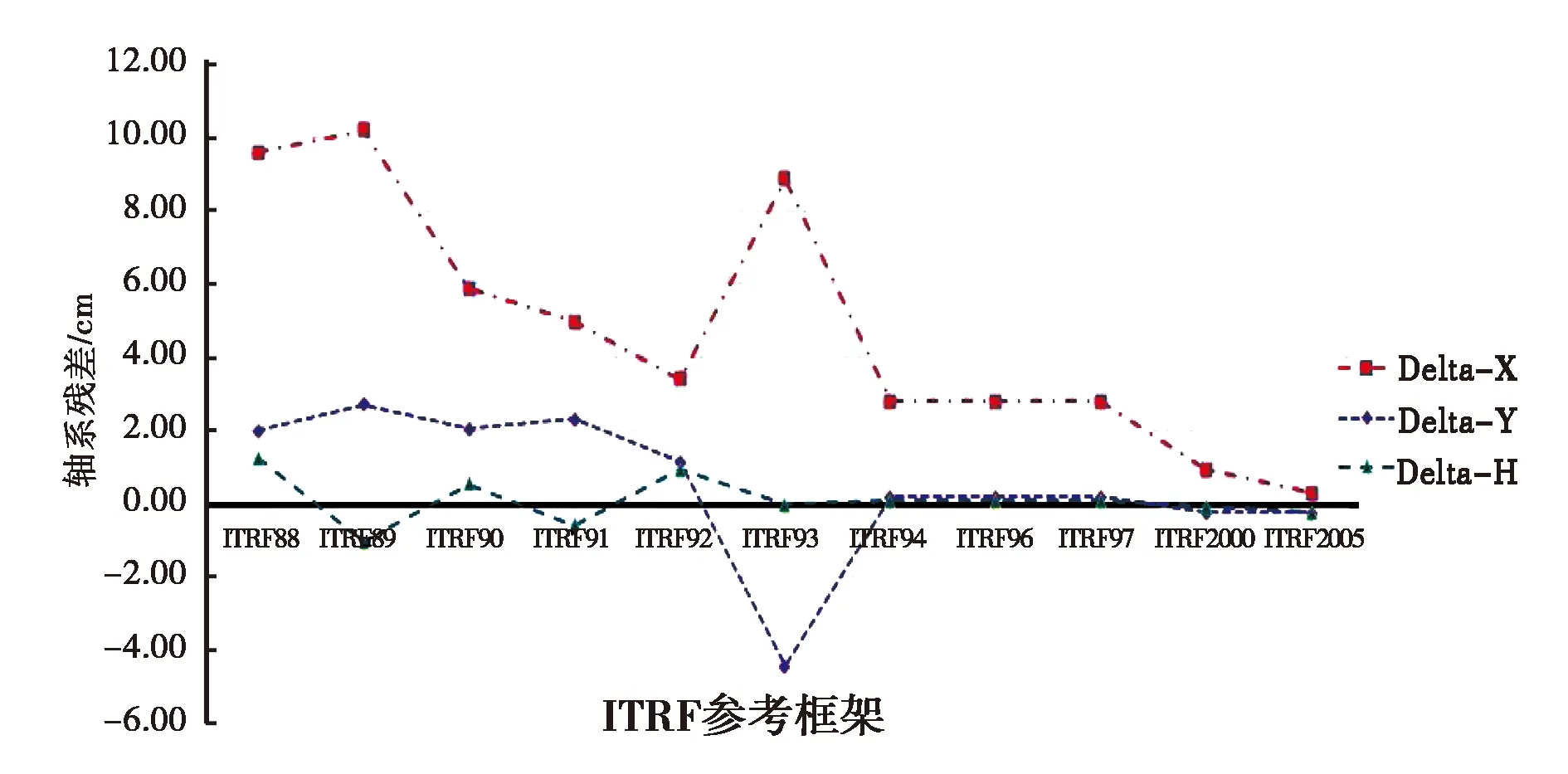
图8 LQC-XN站不同ITRF坐标框架差

通过分析图7、图8可以发现,框架间存在厘米级误差,其中不同的坐标框架,高程相差小于2 cm; ITRF93框架之后框架间的坐标差异较小, 尤其是ITRF97框架以后,差距小于1 cm;而ITRF93由于转换参数与其它框架相比变换太大．所以ITRF93基准下的数据成果与其它基准下的数据成果,存在10 cm左右的平面基准差异．

算例四:用IGS发布的BJFS(2018.613)、LQC-XN(EPH2018.704,速度场信息采用距离较近的12个IGS站的位移变化量按距离反向加权平均求取)站ITRF2008框架坐标和scc周解文件里的位移变化量值进行不同历元下ITRF93框架的坐标变换,可得不同目标历元下的坐标差异如图9、图10所示．

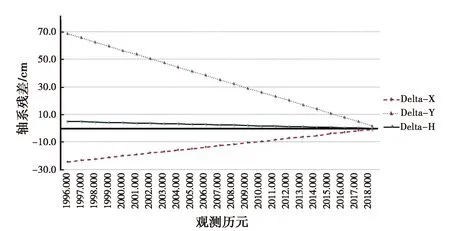
图9 BJFS站历元变化轴系误差变化

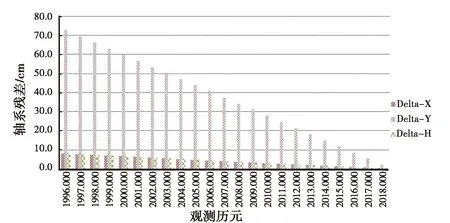
图10 LQC-XN站历元变化轴系误差

如图9～10所示:历元变换坐标误差远大于框架变换坐标误差,其中Y方向坐标变换差异较大;不同的测站由于位移变化量值不一样,历元变换轴系误差也不一样,但变化趋势相同．

算例五:选取CORS站CHDN2016年9月至2018年8月每个月1日、15日的数据进行PPP解算得到相应历元下ITRF2008框架下的三维坐标,并与已知的ITRF93(1996.624)框架下的三维坐标进行对比,如图11所示．采用周边的12个IGS站的速度值按照距离进行反向加权平均,内插得到测站点的速度值进行框架历元变换,得到ITRF93框架下相同历元的三维坐标,并与已知坐标作比较,如图12所示．

图11 CHDN站PPP解与已知坐标差

图12 CHDN站与ITRF框架已知坐标差

如图7～11所示,可以发现不同的测量基准之间存在较大的点位误差,其中历元间差别对坐标分量的影响很大,所以在进行坐标转换时一定要统一历元．通过图12可以发现由于无法得到准确的区域速度场信息,因此进行框架历元变换后,存在6 cm左右的平面误差和15 cm左右的高程误差．

5 实际运用

在某次任务中,选取阵地和落区附近已有的四个成果点LQC-XN(框架历元未知,大地高系统)、LUNAN126(二等GPS水准点、框架历元未知,正常高系统)、I389(ITRF97框架、2000.000历元,大地高系统)、RJ17(ITRF97框架、2000.000历元,大地高系统),利用IGS快速星历进行PPP解算,同时对I389的数据进行框架历元变换并与已知数据作对比,如表3所示．

表3 实测坐标与已知坐标差异cm

从表3可以看出,PPP解与不同基准的数据成果在Y方向存在60 cm左右的框架历元误差,经框架历元归算以后可以得到10 cm以内精度的转换坐标．

以LQC-XN-I389控制网联测为例,利用4台全球卫星导航系统(GNSS)接收机,按照C级GPS网点单基线两测回施测,由于高原测区交通不便,因此GPS测站沿主要道路布设,如图13所示．

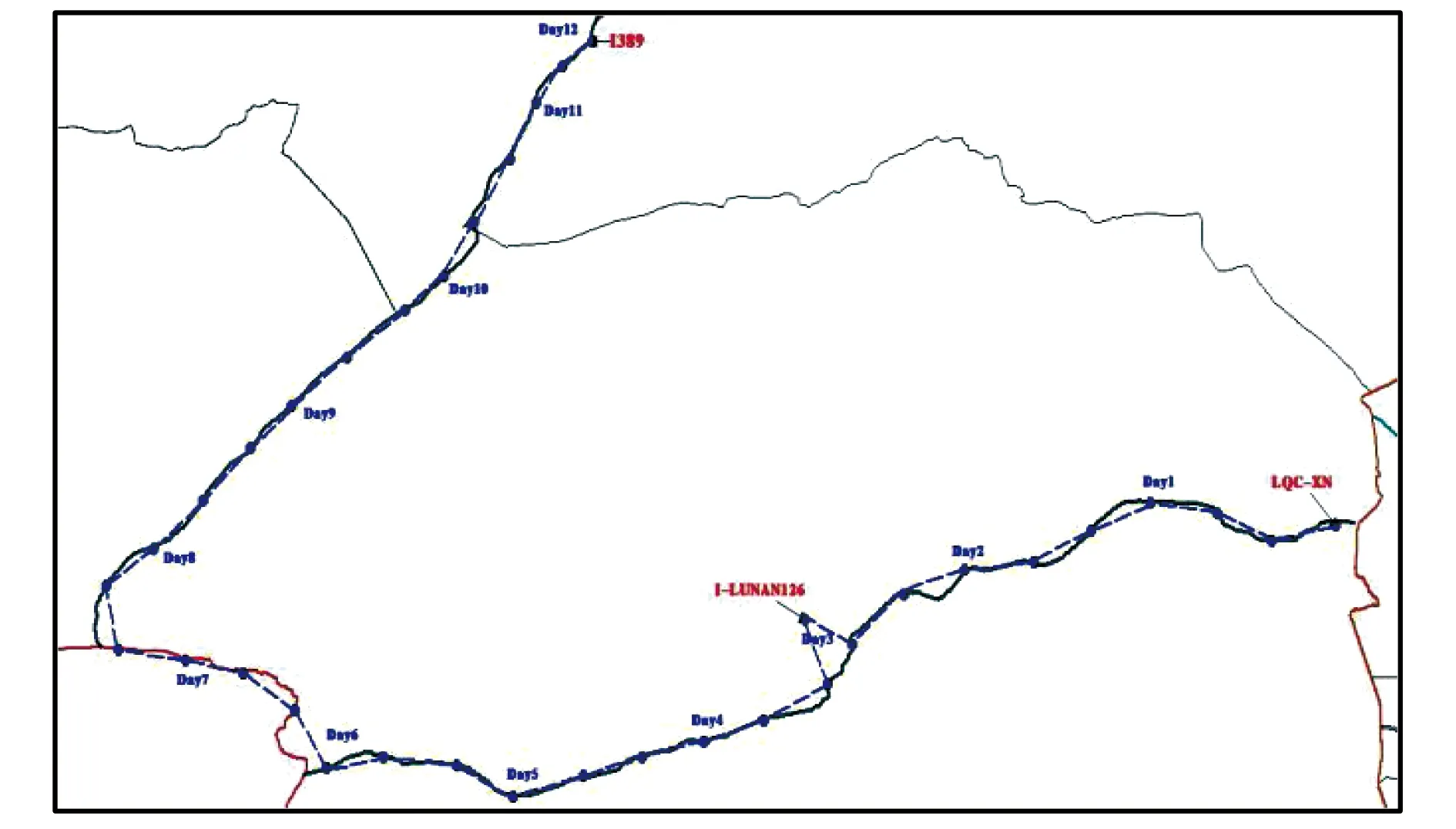
图13 控制网联测路线设计图

从图13中可以看出,完成控制网点联测至少需要12天的时间,且经过700多千米的坐标传递,累计误差将会比较大．而采用PPP布设首级控制网,只需要在阵地和落区分别布设1个独立控制网,用PPP分别求解1～2个控制点,其余2～3个测站可以在后续RTK的基准站位置布设,此时仅需要3天的时间即可以得到ITRF2008坐标框架下的首级控制网点．

6 结束语

在无控制点的测区建立独立坐标系时,利用PPP技术布设首级控制网,可大幅缩短作业周期,且首级控制网点平面平均误差小于1 cm,高程平均误差小于10 cm,可有效满足常规兵器试验点位测量精度．在多基准的测区对已有测量成果进行基准变换时．历元变换对Y方向的影响较大,且由于不同测站的速度场信息不同,导致位移年变化值不尽相同,因此在特殊情况下需采取基准变换时,要注意提高测站点速度值的解算精度．