Finsler-Hadwiger型不等式推广的再研究

王洪燕 郭要红

(安徽师范大学数学计算机科学学院 241000)

1 引言

1919年，Weitzenbock提出了如下不等式：[1]

定理1设a,b,c,S分别是△ABC的边长与面积，则

1937年，Finsler和Hadwiger建立了一个更强的不等式如下：[2]

定理2设a,b,c,S分别是△ABC的边长与面积，则

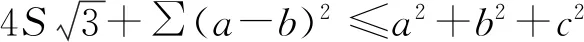
《美国数学月刊》2016年第9期刊登了马其顿人Martin Lukarevski提供的问题11938如下：

问题11938[3]设a,b,c,S,R,r分别是△ABC的边长、面积、外接圆半径、内切圆半径，则

(1)

事实上，1998年武钢高三学生李磊应用Kooi不等式[4]证明了不等式(1)[5]，文[6]已收录不等式(1).

本文对不等式(1)进行研讨，得到如下不等式：

定理3设a,b,c,S,R,r分别是△ABC的边长、面积、外接圆半径、内切圆半径，则

(2)

2 两个引理

为证明不等式(2)，先给出两个引理

引理1(Blundon不等式)[4]设a,b,c,s,R,r分别是△ABC的边长、半周长、外接圆半径、内切圆半径，则

其中等号成立当且仅当三角形为正三角形.

引理2设a,b,c,s,R,r分别是△ABC的边长、半周长、外接圆半径、内切圆半径，则

(3)

其中等号成立当且仅当三角形为正三角形.

证明由引理1可知，只要证

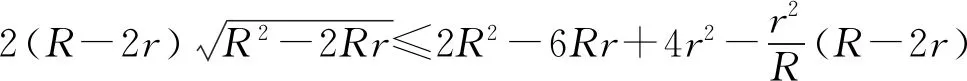
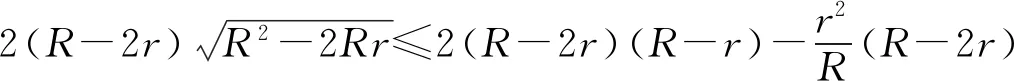
由欧拉不等式：R≥2r,只要证

(4)

因为2(R+r)(R-2r)+3r2≥0，而

=4Rr3+r4≥0.

所以(4)式成立，从而(3)式成立，由以上证明过程可知，(3)式等号成立当且仅当三角形为正三角形.

3 结论的证明

定理3证明

同理可得

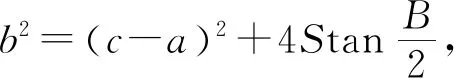
三式相加可得

由三角恒等式

即

利用引理2，由

即有

定理3得证.

4 讨论

根据欧拉不等式：R≥2r，有

所以(2)式是(1)式的加强.

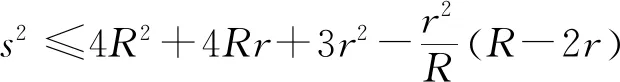
≤4R2+4Rr+3r2.

所以引理2是Gerrentsen不等式[4]s2≤4R2+4Rr+3r2的加强.