基于数学理解性学习的习题课教学①——从学习者差异原则谈起

陈玉娟 季建生

(江苏省常州高级中学 213003)

理解性学习是和我们常说的机械学习、死记硬背的学习相对立的概念,指“学生通过学习获得深刻概念性理解的发展和恰当运用知识的能力”[1].美国国家研究理事会的一份报告《学习与理解：改进美国高中的数学和科学先修学习》中提出理解性学习的七个原则,本文就其中的学习者差异原则,结合笔者的教学实践谈谈数学习题课的教学,请同行不吝赐教.

1 课前,调查设计需先行

习题课是新授课的递进,主要是帮助学生运用已学知识,形成某些数学的解题技巧,加深对数学知识的理解,培养数学思维和数学意识[2].常规的习题课教师常常会用整节课师生共同讨论习题.事实上班级学生是存有差异的,学习差异者原则承认学生处理不同符号系统的偏好和不同能力[3].为此,课前教师应调查、统计、搜集学生学习过程中各方面的情况.

人们常说“抛砖引玉”,从本质上说,例题是“砖”,是载体,其目的是要引出“学生思维”这块“玉”.为此,笔者在关于“椭圆定点、定值及范围问题”的教学中,依据教学目标和要求,结合班级学生一段时间内出现的困惑及错误,按从低到高的难度,归类、设计下面3类例题,适时安排习题课.(课前给予学生例题,由课代表组织学生根据自己的学情,对应于3个例题自主成立3个学习小组.)

图1

图2

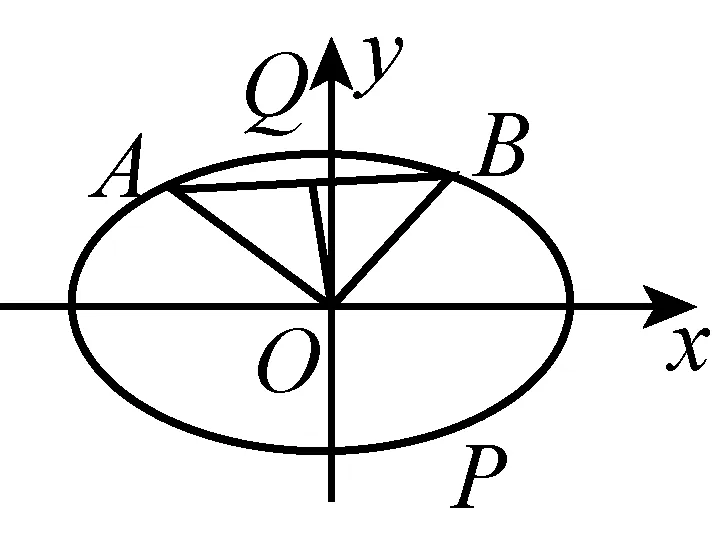
图3

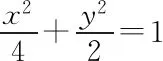
2 课中,载体内容需优选

华东师范大学副教授陈家刚教授提出：“对应于学习者差异原则的教学设计应该利用多元表征,相应设计不同的教学活动”.笔者认为,先进课程理念下的数学习题课因由“关注学生学习结果”转向“关注学生学习活动”.所谓“玉不琢不成器”,要对“玉”用“习题”这把刻刀进行雕琢.“工欲善其事必先利其器”,习题选择、搭配的重要性不言而喻.为此,笔者择典型、分层次、有差异地组织以下教学活动解决相关问题.

2.1 以学为主,逐步铺设台阶,目的性和层次性相结合组织第1组学生活动

普通高中数学课程标准的核心理念是课堂教学要以学生为主体,以促进人的发展为本.第1组学生普遍基础薄弱,例题1的难度并不大,关键在于动态的处理和参数的设立.已知信息中出现两个动点和一条动直线,目标是证明与动点相关的定值问题.为此,笔者从学生的实际出发,设计两个相似类型的典型引例,为他们铺设思维的台阶.

因为题设中只有一个动点,学生很快找到突破口,设“点参”P解决问题.

图4

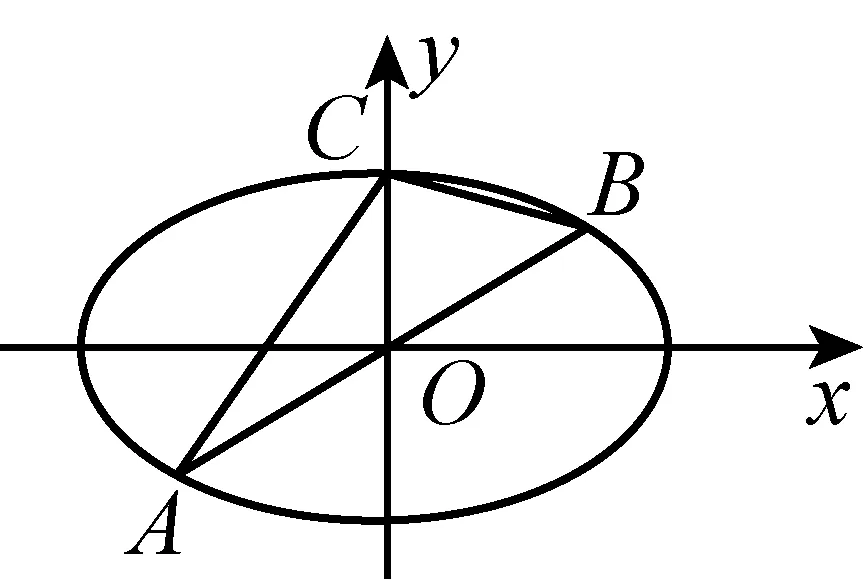
图5

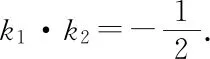
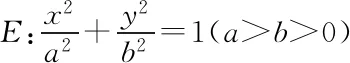
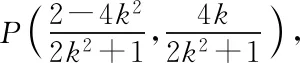
2.2 先学后教,加强变式训练,启发性和针对性相结合组织第2组学生活动

“施教之功,贵在引路,妙在开窍”.要开启学生通窍之门,就要让学生先学,教师根据学情进行引导、点拨,提高针对性和实效性.为此,笔者针对第2组学生设计如下的教学活动.

首先,引导学生分析例2中题设与目标的关键信息：已知动直线过定点(右焦点F),要探求满足条件“CF平分∠ACB”的定点C,该条件就是两者间的联系源,其实质是CA,CB斜率互为相反数,这是本题思维的突破口.

然后,通过本小组学生自主探究,逐步完善,得出如下解答：

因为PF平分∠APB,

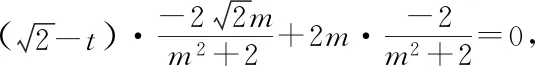
最后,教师设计针对性变式训练,为学生的思维发展提供阶梯,实现“在坚实基础上的有所发展”[4].需要提出的是,其间要给予学生充分思考和探索的时间和空间,让学生在“自审、自评”的过程中暴露问题,动脑、动手学在先,这样,其求知内驱力会大大增强.

图7

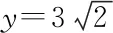
2.3 以学定教,构建学习共同体,全面性和选择性相结合组织第3组学生活动

传统学校教育学习被看成是个人追求,目标是把课本和教师的知识传递给学生.这种学校文化阻碍学生相互讨论,共同解决问题,因而常常妨碍知识的分享.学习共同体理念则强调具有不同专长的学习者和教师结成共同体,围绕学习任务进行互动和协作,学习者清晰表达自己的思维,教师提供相应指导,学习者之间互相帮助,从而支撑学习者个人知识的发展[5].

例3的已知信息中共有4个动点,4条动直线,目标是两个动点间距离的范围.其中有两个联系源,分别是两个垂直关系.考虑到第3组学生的数学基础和素养比较高,笔者就充分给予机会表现他们的知识和技能,此时教师的引导作用在于有的放矢的“甄别选用”和“相机诱导”.下面选用了他们集思广益得出的其中3种解决方案.

方法1设k参,利用方程思想,通过“交轨”法寻求动点的Q轨迹.

设直线AB方程为y=kx+m①,代入椭圆方程得(2k2+1)x2+4kmx+2m2-4=0,

设点A(x1,y1),B(x2,y2),

得(1+k2)x1x2+mk(x1+x2)+m2=0.

所以(1+k2)(2m2-4)-4m2k2+m2(1+2k2)=0，

即 3m2=4(1+k2)②.

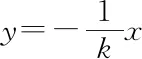
方法2设k参,利用数形结合思想,通过圆的定义直接寻求动点Q的轨迹.

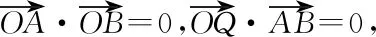
所以OA2+OB2=AB2,OQ·AB=OA·OB.

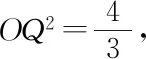
方法3设点参,利用消元转化思想,由定义直接探求动点Q的轨迹.

设点A(x1,y1),B(x2,y2),

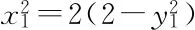
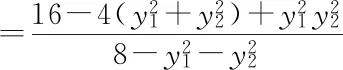
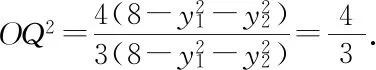
学习共同体需设计便于学生以团队形式互动和协作,获得和发展技能的课堂环境.提供机会使学生与教师或同伴就学科内容进行拓展性的对话交流,挑战彼此观点,重建思维[6].

3 课后,总结评价需跟进

先进课程理念下的数学习题课应由“注重考试分数的终结性评价”转向“注重促进人的发展的过程性评价”.为此,教师还应根据学习者差异设计恰当的学习评价,使具有不同学习风格的学生有各种机会表现他们的知识和技能.

笔者采取的方案是“小题大做”！我们加入“数学写作”学校联盟.习题课后教师组织、指导学生在反思、感悟的基础上进行总结提炼,形成文字,指导学生数学写作.积极参与联盟的第一届写作竞赛活动,高二全年级参与,共征集论文80余篇,择优选送了10篇参与评选,共获得二等奖3篇,三等奖3篇的好成绩，极大提高了学生数学学习的兴趣和自信.笔者认为这也是一种超越分数之上的体现新颖性和创新性的学习评价方式.

结束语

《国家中长期教育改革和发展规划纲要》提出为每个学生提供适合的教育.而适合的前提是有选择,可选择.笔者认为在习题课教学中,教师应设计符合学生不同发展能力、知识基础、爱好和认知风格的课程材料.为不同思维特性的学生提供不同组合的问题,对于同一思维类型的人,针对学习者的能力和兴趣设计不同层次的问题.尝试让不同的人学习不同的数学.只有这样才能体现“为理解而教,为理解而学”,才能帮助学生将学习迁移去解决新的问题,真正实现可持续发展.