数学问题解答

2019年6月号问题解答

(解答由问题提供人给出)

2486已知a≥b≥c>0，求证：

(河南省南阳师范学院软件学院 李居之 孙文雪 473061)

证明由均值不等式得

因为a≥b≥c>0，

所以(a-b)(b-c)(a-c)≥0

⟺a2b+b2c+c2a≥ab2+bc2+ca2

从而原不等式成立，当且仅当a=b=c时等号成立.

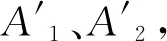
(成都市金牛区蜀汉路369号2-2-35 610036 张殿书)

图1

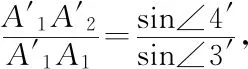
以上各式相乘，又易知∠1=∠1′，∠2=∠2′，∠3=∠3′，∠4+∠4′=180°,∠6=∠2=∠6′，

经化简可得

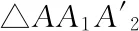
A0x2n+1-A2x2n-1+A4x2n-3-A6x2n-5+…+(-1)nA2nx+(-1)n+1sin(2n+1)α=0

(1)

(河南质量工程职业学院 李永利 467000)

证明正弦的n倍角公式为：

(2)

(见唐秀颖主编．数学解题辞典(三角)[M]．上海辞书出版社，1988年12月第1版，1996年2月第5次印刷，第127页)．

取n为2n+1，则由(2)式可知

(3)

(3)式整理即得方程(1)．

又因sin(2n+1)α=sin[2jπ+(2n+1)α]，

其中j为整数，所以由以上讨论可知方程(1)的解为

2489已知O为锐角△ABC的外心，过O的直线交AB、AC所在的直线于P、Q两点.求证：

(江西省高安市石脑二中 王典辉 330818)

证明如图连接AO并延长交BC于D，连接BO并延长交AC于E，连接CO并延长交AB于F，连接PD、QD.

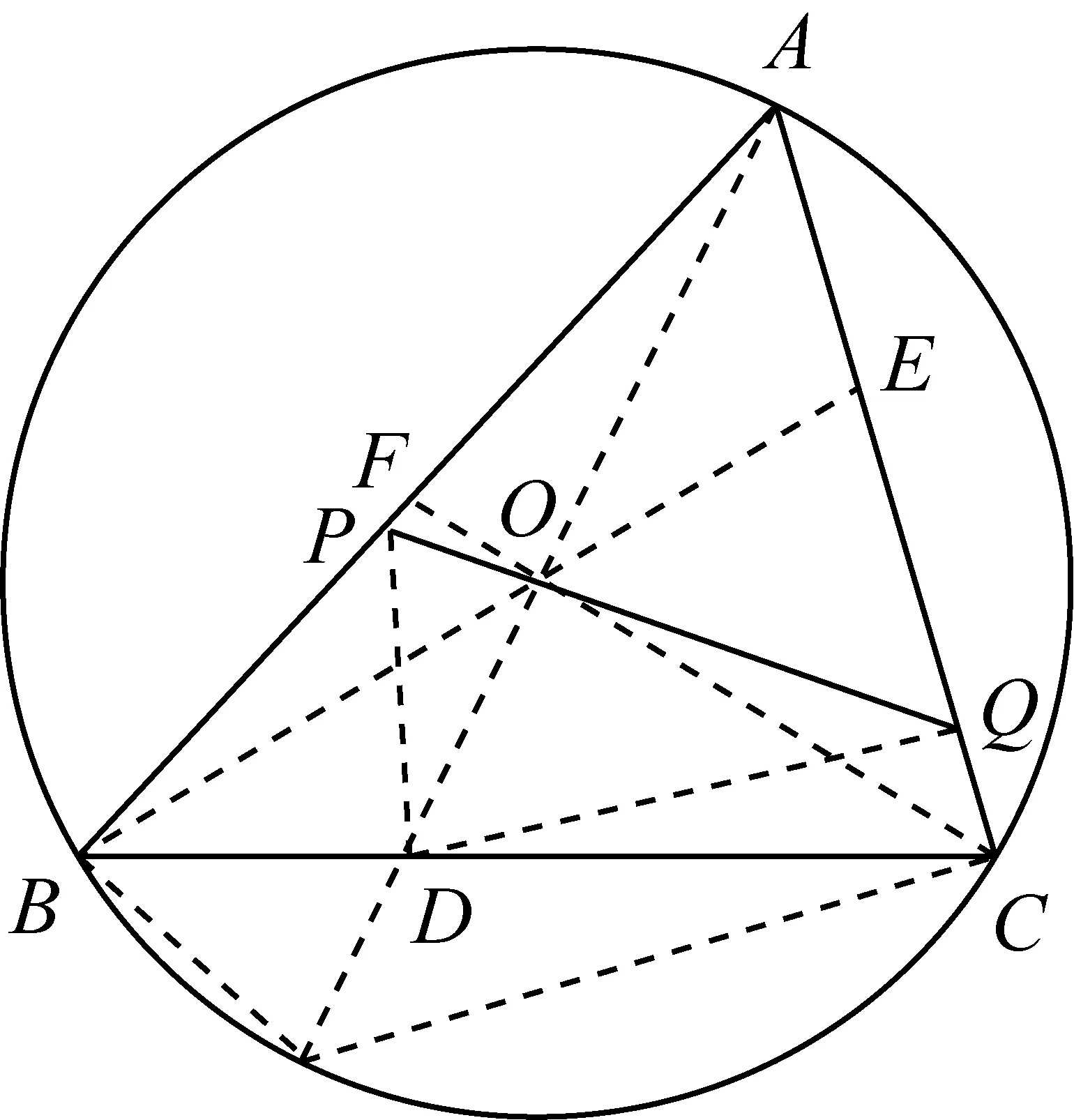
再由合比定理得

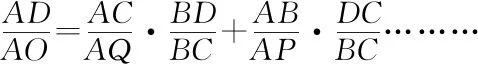
延长AD交△ABC的外接圆于K，

连接BK、CK，

有∠AKB=∠ACB，∠AKC=∠ABC.

因为AK是△ABC的外接圆直径，

所以有∠BAK与∠AKB互余，

∠CAK与∠AKC互余.

因此有

∠BAD=90°-∠AKB=90°-∠ACB，

∠CAD=90°-∠AKC=90°-∠ABC.

又由共边比定理可得

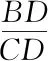
又由梅涅劳斯定理，可得

把②、③、④式代入①，得到

=sin2∠BAC+sin2∠ABC+sin2∠ACB⑤

又因为

sin2∠BAC+sin2∠ABC+sin2∠ACB

=2sin(∠BAC+∠ABC)cos(∠BAC-∠ABC)+2sin(∠BAC+∠ABC)[-cos(∠BAC+∠ABC)]

=2sin(∠BAC+∠ABC)cos(∠BAC-∠ABC)-2sin(∠BAC+∠ABC)cos(∠BAC+∠ABC)

=4sinA·sinB·sinC.

⑤式等价于

=4sinA·sin∠ABC·sin∠ACB.

而利用均值不等式和琴生不等式

≥sin∠BACsin∠ABCsin∠ACB,

等号成立仅当△ABC为等边三角形.

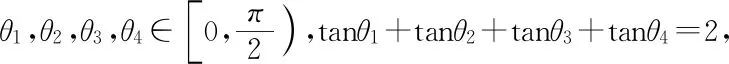
(河南辉县一中 贺基军 453600)

即sinα-2sin2αcosα≥0，

根据均值不等式及上述引理得

sinθ1sinθ2+sinθ3sinθ4

2019年7月号问题

(来稿请注明出处——编者)

2491已知a,b,c≥0,ab+bc+ca=1,求证:

(陕西省咸阳师范学院教育科学学院 安振平 712000)

2942已知，如图，AB、AC，CD、BE交于G，并分别交AB、AC于J、K，DK交AB于H，EJ交AC于I，DI与EH交于F，证明：A、F、G三点共线．

(江西师范高等专科学校 王建荣 335000)

2493求证：在△ABC中，有

上式取等号，当且仅当△ABC为正三角形．

(湖北省谷城县第三中学 贺 斌 李至军 441700)

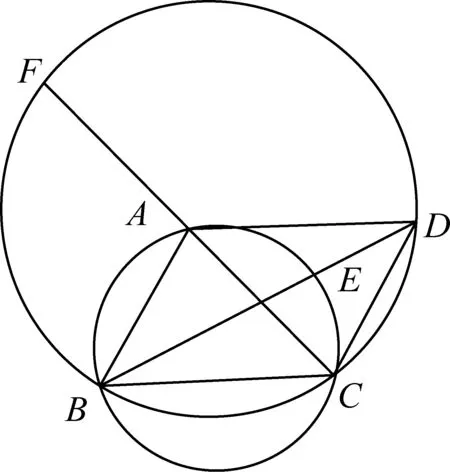
2494ABCD对角线交于点O，线段OD上有点E，线段OA延长线上有点F，求证：BD·BE=AC·CF，A、B、C、E四点共圆，B、C、D、F四点共圆，这三个条件任意知道两个，可得第三个.

(华中师范大学国家数字化学习工程技术研究中心 彭翕成 430079 )

2495设n∈N*且ai>0(i=1,2,…n).证明:

(安徽铜陵市第一中学 陈良骥 244000)