直观助思考 思辨破难题
——2017年新课标Ⅰ导数压轴题剖析及启示
孙 泰
(北京丰台二中 100071)
导数大题是新课标卷的压轴大作,教学中如何突破这道难关?现实中,归类题型的“套路”派和借用高等数学公式、定理的“高观点”派教学方式较为普遍,取得一定的效果,但都遇到了瓶颈,甚至埋下了隐患. 本文以2017年新课标Ⅰ导数题为例,谈谈自己的想法,与大家交流学习,旨为高三解题教学做一些探索.
1 试题呈现
已知函数f(x)=ae2x+(a-2)ex-x.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若f(x)有两个零点,求a的取值范围.
2 策略剖析
“对于任何学科的教学,最终都应当把培养学生的学科直观作为重要的价值取向”[1],史宁中先生这段话指明了解题教学的重要方向,那就是解决数学问题始于直观,终于理念.
策略1几何直观探方向,代数直观妙解题
由(Ⅰ)当a≤0时,f(x)在区间(-∞,+∞)内单调递减,从几何直观的角度分析函数图象下降,不可能与x轴有两个交点,所以函数f(x)不会存在两个零点.
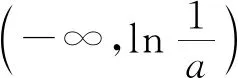
所以要使f(x)有两个零点,必有0 分析f(x0)=ae2x0+(a-2)ex0-x0=ae2x0+aex0+(-2)ex0-x0,代数直观,从组成解析式每部分的值的正负入手,其中含参数部分ae2x0+aex0>0,不含参数部分(-2)ex0<0,-x0>0,只需要找到超越不等式(-2)ex0-x0≥0的一个解,又0 直观感知图象趋势,x→+∞时,ae2x→+∞,(a-2)ex→-∞,-x→-∞,不易判断f(x)的符号,遇到困难. 如何找到呢? 代数直观,简化函数,难点在于函数解析式由超越指数函数和一次函数组合而成,不好处理,利用ex>x(x>0)放缩为可解方程,统一为超越形式 f(x0)=ae2x0+(a-2)ex0-x0 >ae2x0+(a-2)ex0-ex0 策略2代数直观巧变换,几何直观助解题. f(x)=ae2x+(a-2)ex-x零点问题的代数变换方向有: 令h(x)=1-x-ex, 则h′(x)=-1-ex<0,又h(0)=0, 当x∈(-∞,0),h(x)>0; 当x∈(0,+∞),h(x)<0. 所以g(x)max=g(0)=1. 直观感知图象趋势,x→-∞时,ex→0,x→-∞,因此g(x)→-∞;x→+∞时,e2x→+∞,ex→+∞,x→+∞,不能直接判断,要么函数变形 h′(x)>0;当x∈(1,+∞),h′(x)<0, 分析函数g(x)=a(ex+1)的图象,参数a的几何意义是由函数y=ex+1到g(x)=a(ex+1)的伸缩变换系数. 如图,当a=0时及a<0时,图象直观看得清楚,代数论证也不困难. 当a>0时,从几何直观开始. 当0 先证明函数g(x)与h(x)图象在(-∞,0)上有一个交点. 至此得到函数g(x)与h(x)图象在(-∞,0)上有一个交点.严谨吗?正确吗?对于一般函数g(x)与h(x)在(-∞,0)上都是增函数,这个我们借助直观而运用的“定理”对吗?当g(x)=x且h(x)=x+sinx发现这个“定理”不正确.此题观察图象会发现函数g(x)与h(x)图象一凸一凹,递增的速度一快一慢,直观应当正确,如何表述明白呢?建模构造差函数,研究单调性质,利用零点判定定理可以论证的清清楚楚了. 再证明函数g(x)与h(x)图象在(0,+∞)上有一个交点. 先从几何直观出发,借助图象寻找那个困难的x0>0且g(x0)-h(x0)>0, 由于不知道差函数的单调特征,严谨的证明还要构造差函数研究. 变换3.设t=ex,f(x)=ae2x+(a-2)ex-x零点个数问题等价于g(t)=at2+(a-2)t-lnt的零点个数问题,换元法,实现函数结构的变换,成功与否的关键是变换后的函数是否简单、熟悉了. 换元后的函数由二次函数和对数函数组成,研究函数g(t)=at2+(a-2)t-lnt, 当a≤0,g′(t)<0,则g(t)单调递减; 换元后函数g(t)由二次型函数和对数函数构成,一动一静凸凹有别,导函数熟悉、亲切. 对于此函数同上面函数类型相似的变换,得到一系列解决方法,不赘述. 课本是试题的根本来源,高考试题题在卷面上,根在课本内,高考命题原则是:考查基础,立足稳定的基础上创新,那么靠什么保证基础,靠什么决定稳定,不是试题不变,题型不变,而是课本,课本中不仅有稳定的知识,经典的方法,引申的结论,同时蕴含着重要的数学思想方法.回归课本,不是拘泥于课本,单一的回顾知识、方法,而是站在整体的高度诠释系统的知识,让不同的知识交汇,建构起知识的立体网络,让学生思维骋驰在四通八达的立体高速公路上,最终到达数学的巅峰. 教学重视知识、技能、方法的同时,要领悟数学的思想、经历数学的思维分析、解决数学问题过程,以数学思想为魂,统领复习,这样才能参透通性通法,而不是陷入同型同法的简单重复和模仿,解题僵化,纵使刷题无数,遇到新问题,还是遭遇无法解决的囧地.如在函数导数的教学中,加强数形结合、分类讨论、函数方程、数学建模、转化化归思想和极限思想的运用,加强空间想象能力、抽象概括能力、数学运算能力、推理论证能力和分析问题解决问题能力的提升,加强形象思维、抽象思维(形式思维和辩证思维)、直觉思维和创造思维培养. 郑毓信教授认为,数学核心素养的基本涵义就在于:我们应当通过教学活动帮助学生学会思维,并能使他们逐步学会想得更清晰、更深入、更全面、更合理. 不可忽视教学活动中,不断积累、浓缩、升华基本活动经验,培养既有形象性、可视性又有整体性的数学直观(几何直观、代数直观),形成直观—抽象—推理—直观的螺旋发展模式,真正进入深度学习. 而现实教学,解题中遇到难以突破的关口,诸如套用题型“通性通法”,蒙混过关,借用高等数学公式、定理工具,表面完美解决,实则不解其意,这样的教学,以分数为目标,到头来终是难得高分,更可惜的是断送学生面对思维受阻,山穷水复疑无路,不断探索,攻坚克难百折不挠后,柳暗花明又一村的宝贵心路体验,养成追求简捷与形式优美的思维方式和行为习惯的机会. 著名数学家柯朗在《什么是数学》一书开篇写道:“数学,作为人类思维的表达形式,反映了人们积极进取的意志、缜密周详的推理以及对完美境界的追求. 它的基本要素是:逻辑和直观、分析和构作、一般性和个别性,虽然不同的传统强调不同的侧面,然而正是这些互相对立的力量的相互作用以及它们综合起来的努力才构成了数学科学的生命、用途和它的崇高价值”,这段激荡人心的文字启示我们展示数学基本要素和人们积极进取的意志、缜密周详的推理以及对完美境界的追求的数学教学,不仅是高效的教学,更是愉悦我们心智的精神饕餮,学会思考的教学才最有价值.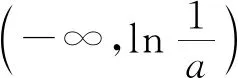
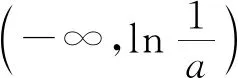
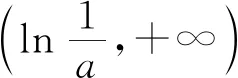
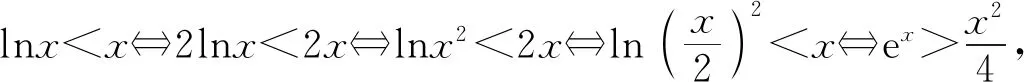









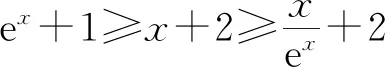
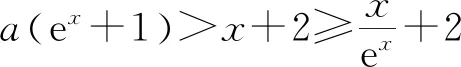



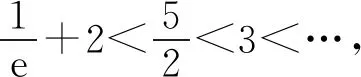


3 教学启示
3.1 回归教材,筑牢根基,优化知识结构
3.2 深化思想,提高能力,优化思维品质
3.3 落实素养,积累经验,构建深度学习
4 结束语

