YRT转台轴承摩擦力矩特性研究
张占立, 周鹏举, 李文博, 王恒迪
(河南科技大学 机电工程学院, 河南 洛阳 471003)
0 引言
YRT转台轴承是一种可承受联合载荷的高精度三排滚子转盘轴承,广泛应用于坦克、军用雷达等精密仪器的回转部位[1]。YRT转台轴承摩擦力矩的大小和稳定性直接影响回转部件的旋转精度和性能。因此摩擦力矩已成为其设计中非常重要的技术指标[2]。
目前,国内外对三排滚子转盘轴承的研究主要集中在载荷分布、承载能力、寿命等方面。Aguirrebeitia等[3]在考虑轴承轴向载荷和倾覆力矩的情况下,建立了轴圈力和力矩平衡方程,并在此基础上提出了一种计算三排滚子转盘轴承极限载荷的方法。Göncz等[4-5]使用非线性弹簧单元代替滚子,建立了三排滚子转盘轴承的有限元分析模型,分析计算了滚道表面下的接触应力,在此基础上计算了滚道的疲劳寿命,建立了三排滚子转盘轴承的静态、动态承载能力计算模型。冯建有等[6]研究了三排滚子转盘轴承滚子与滚道间非理想Hertz接触特性,得出了接触变形及应力沿滚子轴向的变化规律。李云峰等[7]在数值分析和有限元分析的基础上,建立了三排滚子转盘轴承的校核计算方法。于春来等[8]提出了一种三排滚子转盘轴承的寿命计算方法。现有针对三排滚子转盘轴承的研究,在计算载荷分布时均未考虑滚子修形对载荷分布的影响。此外,在三排滚子转盘轴承摩擦力矩的研究方面,现有文献中尚未涉及。鉴于此,本文在考虑滚子修形的情况下,采用切片法建立其在联合载荷下的静力学模型,并在此基础上建立了YRT转台轴承摩擦力矩模型。研究了工况参数、轴向游隙和滚子修形对YRT转台轴承摩擦力矩的影响规律。
1 YRT转台轴承静力学模型
如图1所示,YRT转台轴承由两列轴向滚子、一列径向滚子、外圈、第1内圈、第2内圈组成。其中两列轴向滚子主要承受轴向载荷,径向滚子主要承受径向载荷。第1内圈与第2内圈通过螺钉连接组成轴承内圈。在工作过程中,轴承外圈固定,内圈旋转。
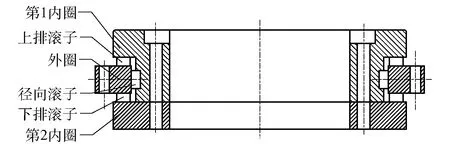
图1 YRT转台轴承结构示意图Fig.1 Structure of YRT rotary table bearing
在对YRT转台轴承进行静力学分析的过程中,忽略内圈装配螺钉的影响,假设内圈为一整体,简化YRT转台轴承结构。并假设轴承外圈固定,内圈旋转。轴承在轴向力Fa、径向力Fr和倾覆力矩M0的作用下,内圈产生轴向位移δa、径向位移δr和转角位移α. 其几何干涉模型如图2所示,图中ψ为各排滚子的位置角,dm为轴承节圆直径。
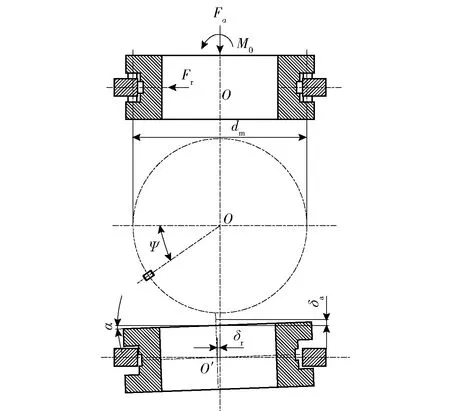
图2 受载几何干涉模型Fig.2 Loaded geometric interference model
1.1 受力分析
由于在YRT转台轴承中,滚子与滚道间的接触不是理想线性接触,故采用切片法计算滚子与滚道间的接触力可以得到更精确的数值解[9]。将各排中的每一个滚子等分为n片,每个切片的厚度为w=l/n,l为滚子有效长度。
在联合载荷的作用下,上排第i个滚子第j片中心处两滚道面间的法向趋近量为
(1)
下排第i个滚子第j片中心处两滚道面间的法向趋近量为
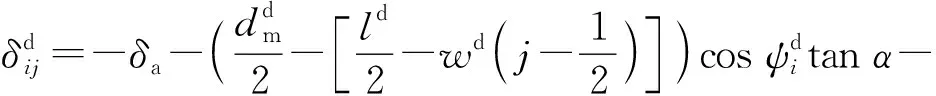
(2)
式中:上标d代表下排滚子。
径向排第i个滚子第j片中心处两滚道面间的法向趋近量为
(3)
式中:上标m代表径向排滚子;ur0为径向初始游隙。
由此可得,每一切片滚子处的法向载荷[9]为
(4)
则各排中第i个滚子所承受的法向载荷为
(5)
1.2 轴承平衡方程
为确定各排中各个滚子的载荷,需建立轴承的平衡方程。YRT转台轴承的内圈在轴向力Fa、径向力Fr、倾覆力矩M0和各排滚子滚道间接触力的联合作用下处于平衡状态。
由此可得,其内圈轴向平衡方程为
(6)
其内圈径向平衡方程为
(7)
其内圈力矩平衡方程为
(8)
将(1)式~(5)式代入(6)式~(8)式中,使用Newton-Raphson法,代入YRT转台轴承尺寸参数,求得其在轴向载荷Fa、径向载荷Fr和倾覆力矩M0的作用下,内圈的轴向位移δa、径向位移δr和转角位移α,进而求出各排各个滚子每一切片处所承受的载荷。
1.3 运动分析
由于YRT转台轴承转速较低,因此将上排、下排滚子在节圆处与滚道之间的相对运动视为纯滚动。如图3(a)所示,x轴为YRT转台轴承的中轴线,O点为YRT转台轴承的几何中心点。A点、B点分别为上排滚子在轴承节圆处与内、外滚道的接触点,C点、D点分别为下排滚子在轴承节圆处与内、外滚道的接触点。A点、B点、C点、D点处,滚子与滚道的相对运动均为纯滚动。图3(b)中ωI为内圈角速度,ωE为外圈角速度,ωc为滚子公转角速度,ωr为滚子自转角速度,Dw为滚子直径,yij为第i个滚子第j片中心到轴承中心的距离。

图3 YRT转台轴承运动示意图Fig.3 Movement of rotary table bearing YRT
根据无滑动条件可得,上、下两排滚子的自转和公转角速度分别为
(9)
(10)
由于轴承上排、下排滚子与滚道接触线上各点处的线速度不同,所以上排、下排滚子与滚道接触部分在节圆两侧必将存在相对滑动。由图3(b)可得上排、下排第i个滚子第j片处与内、外圈滚道间的相对滑动速度为
(11)
(12)
上排、下排第i个滚子在轴承节圆处与内、外滚道间的平均速度为
(13)
(14)
对于径向排滚子,由于滚道上沿滚子与滚道接触线方向上的线速度不变,故不考虑滚子与滚道间的相对滑动。根据无滑动条件可得径向排滚子的自转速度、公转速度分别为
(15)
(16)
径向排第i个滚子与内、外滚道间的平均速度为
(17)
(18)
2 YRT转台轴承摩擦力矩
YRT转台轴承在运转过程中,其摩擦力矩主要由3个方面的因素构成:因材料弹性滞后产生的滚子与滚道之间的滚动摩擦;滚子与滚道之间的滑动摩擦;润滑剂的黏性摩擦。根据轴承发热产生的机理,各部分摩擦力产生的同时必将伴随着能量损失。因此在求得各部分摩擦造成的能量损失之后,再根据能量守恒定律即可求得各部分的摩擦力矩。
2.1 滚子与滚道间的滚动摩擦
由于材料存在弹性滞后,当滚子在滚道上滚动时,滚子与滚道接触区域前半部分压力对滚子滚动的阻力矩大于接触区域后半部分压力对滚子的推力矩,从而产生滚动摩擦力矩[10]。
在YRT转台轴承的运转过程中,各排滚子滚道间由材料的弹性滞后产生的能量损失[11]为
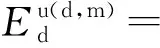
(19)
式中:ξ为材料弹性滞后系数,对钢可取ξ=0.01;η为两接触体的综合弹性常数。
根据能量守恒定律,由弹性滞后产生的滚动摩擦力矩为
(20)
2.2 滚子滚道间的滑动摩擦
由于在YRT转台轴承运转的过程中,滚子和滚道间接触处的线速度不完全一致,从而产生滚子与滚道面间的微观滑动(即差速滑动),由差速滑动产生的摩擦力称为滑动摩擦力。
在YRT转台轴承运转过程中,各排滚子与滚道相对滑动产生的能量损失[12]为
(21)
式中:μij为油膜拖动系数,由弹流拖动系数和边界润滑摩擦系数通过油膜参数插值得到[13-14]。
根据能量守恒定律,滑动摩擦力矩为
(22)
2.3 润滑剂黏性摩擦
YRT转台轴承滚子与滚道间由于润滑脂的黏性阻力引起的能量损失[15]为
(23)
式中:E0为滚子与滚道的当量弹性模量;R0为等效曲率半径;U为滚动体与内、外圈的速度参数;G为滚动体与内、外圈的材料参数;W为滚动体与内、外圈的载荷参数。
其中U、G、W的计算方法为:
(24)
η0为润滑脂的动力黏度;
(25)
α′为润滑脂黏压系数;
(26)
根据能量守恒定律,由润滑剂黏性引起的摩擦力矩为
(27)
2.4 轴承总摩擦力矩
将YRT转台轴承在运转过程中产生的各部分摩擦力矩进行叠加,即可得到YRT转台轴承运转过程中的总摩擦力矩。其总摩擦力矩为
M=Md+Ms+Mr.
(28)
3 YRT转台轴承摩擦力矩试验
3.1 试验装置及试验方法
为验证本文的摩擦力矩模型,自行研制了一台YRT转台轴承摩擦力矩测试装置,如图4所示。在进行摩擦力矩测量时,被测试的YRT转台轴承内圈安装在法兰盘上,法兰盘与主轴连接。调速电机带动主轴旋转,主轴带动法兰盘旋转,从而带动YRT转台轴承内圈旋转。测量轴承摩擦力矩时,拉杆一端与轴承外圈安装孔连接,另一端连接高精度拉力计,从而使轴承内圈旋转、外圈固定,进而测得轴承运转时产生的摩擦力,最终求得轴承运转过程中的摩擦力矩值。

图4 YRT转台轴承摩擦力矩试验台Fig.4 Friction torque test bench of YRT rotary table bearing
3.2 试验轴承参数
采用某装备用YRT80转台轴承,轴承材料为GCr15,滚子采用直线修形,轴承润滑方式为脂润滑,选用牌号为GA08的润滑脂。轴承主要参数如表1所示。

表1 YRT转台轴承主要参数
3.3 试验结果及分析
在工况为空载、外圈固定、内圈旋转的情况下,分别测量其在不同转速和不同游隙下的摩擦力矩,并与理论分析值进行对比。
当轴向游隙为-2 μm、转速nI为5~70 r/min时,YRT转台轴承摩擦力矩的试验值及相应的理论计算值如图5所示。当转速为5 r/min、轴向游隙ua0为-6~0 μm时,YRT转台轴承摩擦力矩的试验值及相应的理论计算值如图6所示。
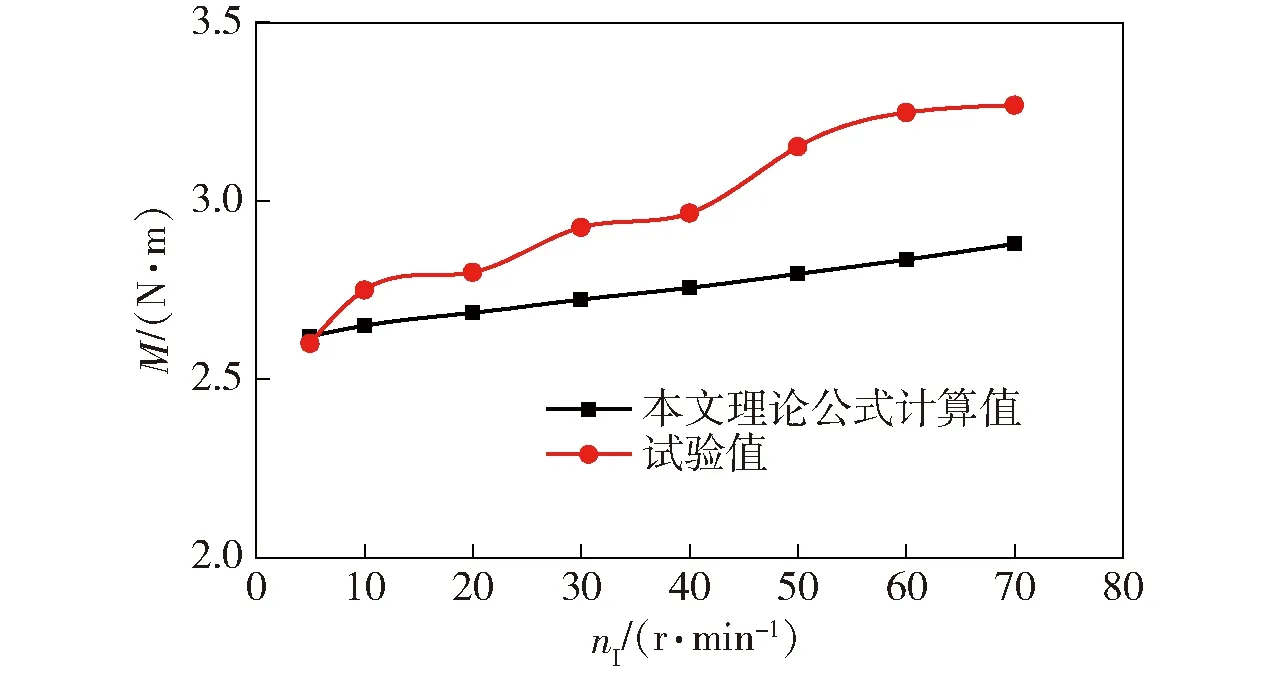
图5 转速对YRT转台轴承摩擦力矩的影响Fig.5 Effect of rotating speed on the friction torque of YRT rotary table bearing
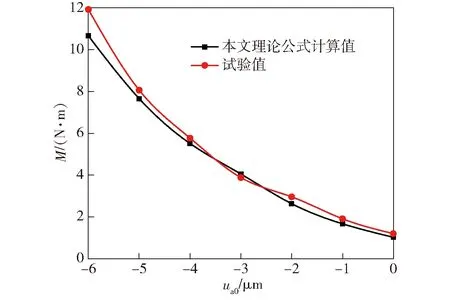
图6 负轴向游隙对YRT转台轴承摩擦力矩的影响Fig.6 Effect of negative axial clearance on the friction torque of YRT rotary table bearing
由图5和图6可以看出:本文对YRT转台轴承摩擦力矩的计算值与试验值变化趋势基本一致;在不同转速下,试验值与理论值的最大误差为14.6%;在不同游隙下,试验值与理论值的最大误差为17.7%. 说明本文建立的模型能够较准确地计算YRT转台轴承的摩擦力矩。产生误差的主要原因是计算中未考虑滚子与保持架之间产生的摩擦,此外在试验过程存在系统误差也可能使得测量值存在误差。
4 YRT转台轴承摩擦力矩特性分析
以试验所用YRT80转台轴承为例,分析工况参数、轴向游隙和滚子修形对轴承摩擦力矩特性的影响规律。
4.1 工况参数对YRT转台轴承摩擦力矩的影响
4.1.1 轴向载荷对YRT转台轴承摩擦力矩的影响
在转速为5 r/min,初始轴向游隙为-2 μm的条件下,YRT转台轴承摩擦力矩与轴向载荷的关系曲线如图7(a)所示。由图7(a)可知,当轴承承受轴向载荷时,上排滚子产生的摩擦力矩占主要部分,下排滚子产生的摩擦力矩次之,径向排滚子产生的摩擦力矩最小。随着轴向载荷的增加,上排滚子产生的摩擦力矩逐渐上升,并逐渐趋近于总摩擦力矩,下排滚子摩擦力矩逐渐减小,并逐渐趋近于一稳定值,径向排滚子摩擦力矩基本保持一较小的稳定值。轴承总摩擦力矩随着轴向载荷的增加逐渐增大,且存在一拐点,该点前后摩擦力矩与轴承轴向载荷基本呈线性关系,该点之前轴承总摩擦力矩与轴向载荷间的比例系数较小,轴承总摩擦力矩较稳定,该点之后比例系数较大,轴承总摩擦力矩急剧上升。
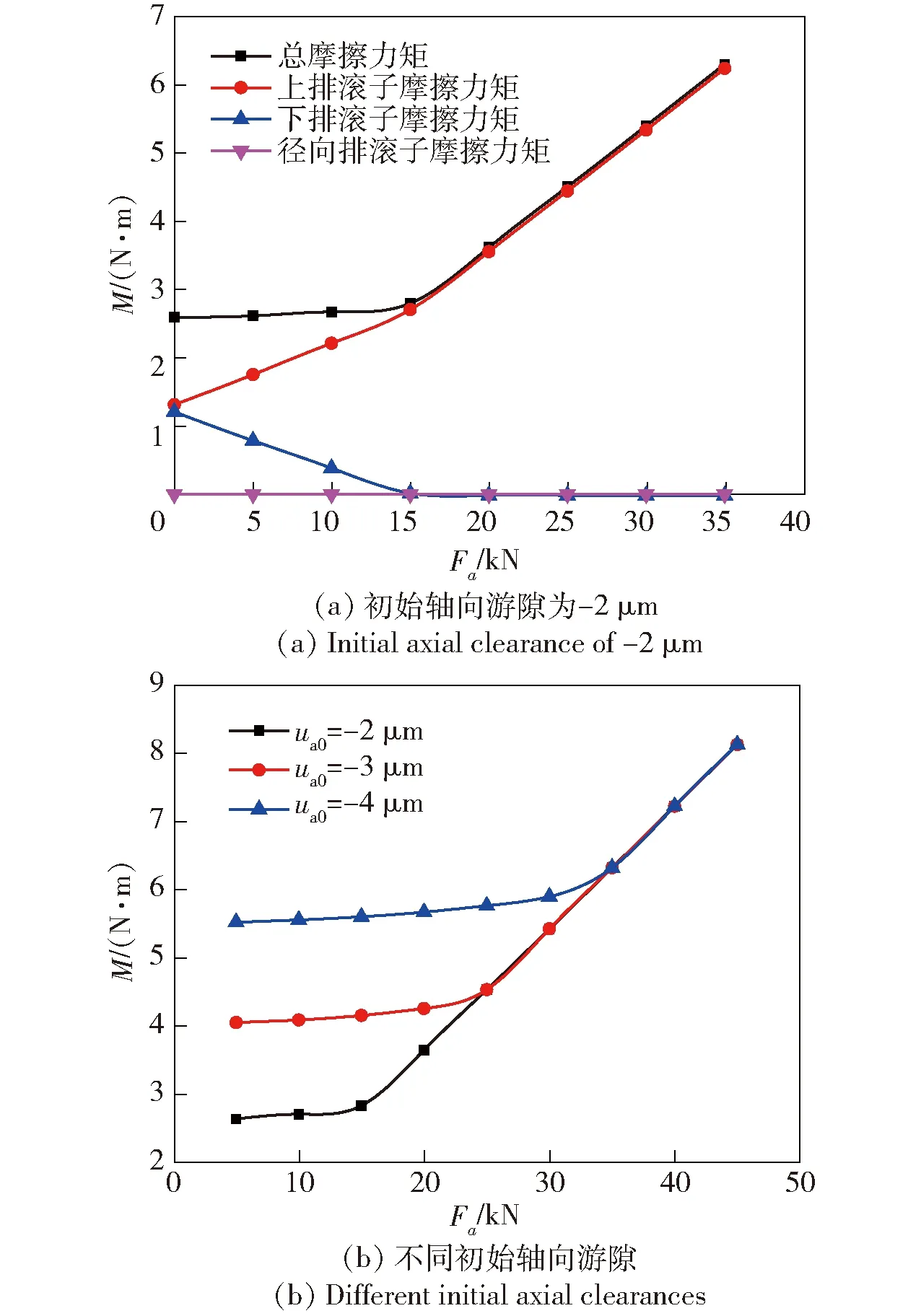
图7 轴向载荷对YRT转台轴承摩擦力矩的影响Fig.7 Effect of axial load on the friction torque of YRT rotary table bearing
这主要是因为随着轴向载荷的增大,轴承内圈的轴向位移逐渐增大,从而使得上排滚子的变形量逐渐增加,承受的载荷逐渐增大,故上排滚子产生的摩擦力矩逐渐增大。下排滚子最初由于负游隙产生的变形量,随着内圈轴向位移量的增大而逐渐被抵消,因此下排滚子承受的载荷逐渐减小直至完全不受载。故下排滚子产生的摩擦力矩逐渐减小,并最终趋于一个稳定的值,这部分摩擦力矩是由润滑剂黏性产生的。当下排滚子不承受载荷之后,轴承刚度减小,随着轴向载荷增加上排滚子变形量加剧,承受的载荷急剧增大,从而造成其摩擦力矩急剧增大,因此其摩擦力矩曲线存在一拐点。对于径向排滚子,其主要承受径向载荷。在仅施加轴向载荷时,径向滚子承受的载荷为0 N,因此其摩擦力矩值保持不变,这是由于润滑剂的黏性而产生的摩擦力矩。
不同轴向游隙下,YRT转台轴承的摩擦力矩与轴向载荷的关系曲线如图7(b)所示,从图中可以看出,随着轴向游隙的减小,轴承总摩擦力矩随轴向载荷变化曲线的拐点后移,且在拐点之前随着轴向载荷的变化,轴承总摩擦力矩数值变化范围较小。与此同时拐点之前轴承总摩擦力矩随着轴向游隙的减小而逐渐增大,但在该点之后趋于一致。因此当YRT转台轴承承受的轴向载荷波动范围较大时,应在摩擦力矩允许的范围内,尽量使用较小的轴向游隙,使YRT转台轴承的摩擦力矩具有更好的稳定性。
4.1.2 转速对YRT转台轴承摩擦力矩的影响
由于YRT转台轴承工作转速较低,故分析其在5~70 r/min转速下,摩擦力矩与转速的关系。轴承空载、初始轴向游隙为-2 μm时,YRT80转台轴承在不同转速下的摩擦力矩变化趋势如图8所示。

图8 转速对YRT转台轴承摩擦力矩的影响Fig.8 Effect of rotating speed on the friction torque of YRT rotary table bearing
由图8可以看出,轴承的总摩擦力矩随着轴承转速的增大而逐渐增大,但其数值变化幅度较小。这是由于随着轴承转速增大,一方面由润滑脂引起的黏性阻力增大,另一方面由图9可知,随着转速的增大,滚子与滚道间的相对滑动增大,从而造成轴承的摩擦力矩逐渐增大。但是由于转速变化的区间较小,因此轴承的总摩擦力矩增幅较小。

图9 滚子沿母线方向与滚道间的相对滑动速度Fig.9 Relative sliding speed between roller and raceway along the generatrix
4.2 轴向游隙对YRT转台轴承摩擦力矩的影响
在转速为5 r/min、不施加任何载荷的条件下,YRT转台轴承的摩擦力矩与轴向负游隙的关系曲线如图10所示。

图10 负轴向游隙对YRT转台轴承摩擦力矩的影响Fig.10 Effect of negative axial clearance on the friction torque of YRT rotary table bearing
由图10可以看出,轴承的摩擦力矩随着轴向游隙的减小而逐渐增大,并且增幅逐渐增大。这是由于随着轴向游隙的减小,上排、下排滚子与滚道间的接触变形逐渐增大,接触载荷也随之增大,从而导致摩擦力矩逐渐增大。
4.3 滚子修形对YRT转台轴承摩擦力矩的影响
滚子修形对滚子表面压力分布有很大影响,滚子上压力分布的差异,将造成轴承运行过程中摩擦力矩的变化,从而对轴承整体的摩擦功耗产生影响。基于此,采用不同的滚子类形,对YRT轴承的摩擦力矩进行研究。
在轴向游隙为-2 μm、轴向载荷为10 kN条件下,使用不同修形滚子时,YRT转台轴承上排滚子沿滚子长度l方向的接触压力q如图11所示。由图11可以看出:当使用直线滚子时,滚子上接触压力均匀分布;使用对数修形滚子时,滚子两端接触压力变小;使用全凸圆弧修形滚子时,滚子两端的接触压力显著减小。
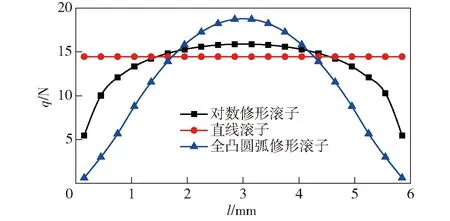
图11 不同修形滚子沿母线方向接触压力分布Fig.11 Contact pressure distributions of different roller crowned types along the busbar direction
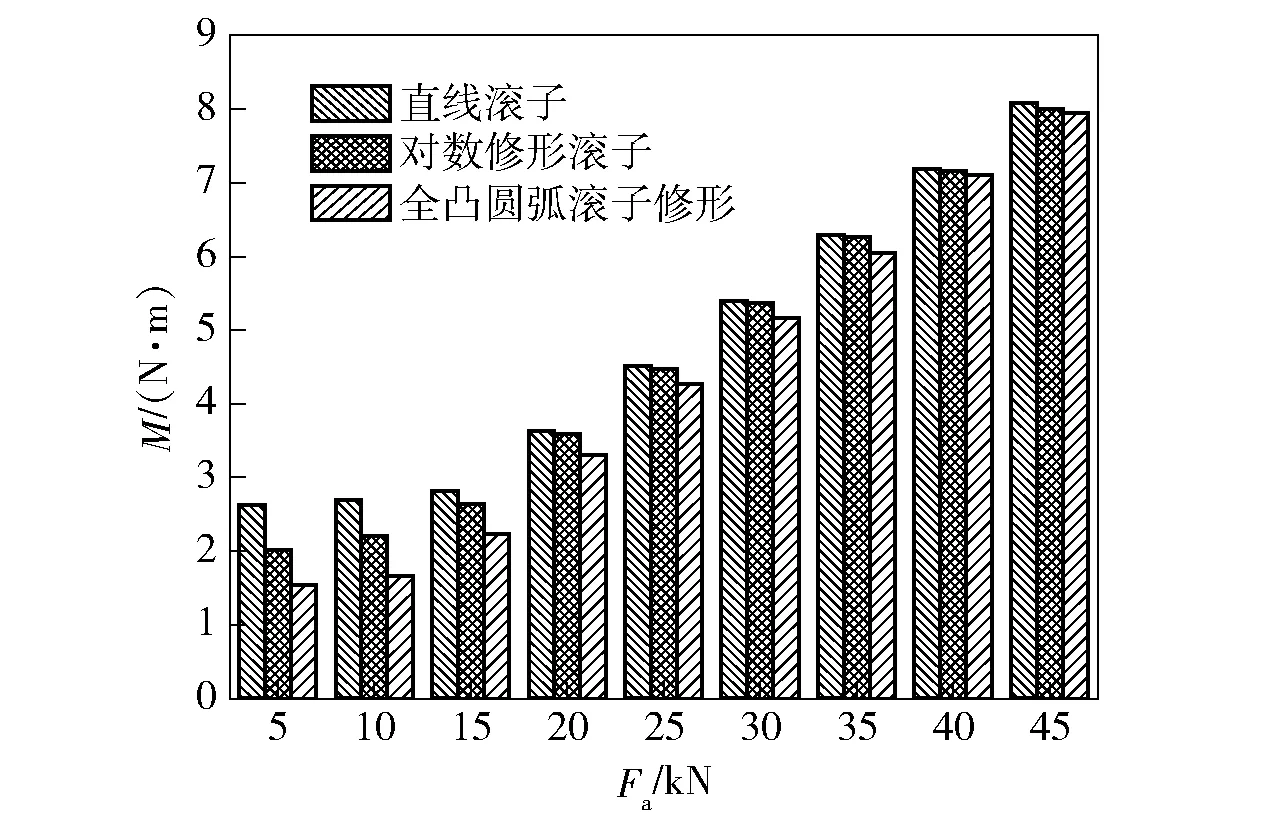
图12 滚子修形对YRT转台轴承摩擦力矩的影响Fig.12 Effect of roller crowned type on the friction torque of YRT rotary table bearing
在不同轴向载荷下,YRT转台轴承使用直线滚子、对数修形滚子和全凸圆弧修形滚子的摩擦力矩如图12所示。从图12中可以看出,在不同轴向载荷下,轴承使用全凸圆弧修形滚子时的摩擦力矩总是最小,对数修形滚子的摩擦力矩次之,直线滚子的摩擦力矩最大。这是由于滚子修形有利于改善滚子两端压力分布状况,使滚子两端接触负荷减小,降低了轴承在运转过程中的摩擦能耗,从而减小轴承的摩擦力矩,且由上文可知全凸圆弧修形对滚子两端压力分布的改善作用最佳。但是,当载荷较小时,三者之间的摩擦力矩相差较大;当载荷较大时,三者之间的摩擦力矩相差较小。这是由于当载荷较小时,不同修形滚子表面的压力差值较大;当轴向载荷较大时,滚子上的接触压力随之增大,但不同修形滚子表面的压力差值较小,滚子修形对滚子两端压力分布的改善作用减弱。因此,在满足YRT转台轴承承载能力的情况下,应优先选用全凸圆弧修形滚子,从而有效降低YRT转台轴承的摩擦力矩。
5 结论
1)YRT转台轴承在承受轴向载荷时,其摩擦力矩主要由上排滚子产生,且轴承总摩擦力矩曲线存在一拐点,拐点前后摩擦力矩与轴向载荷基本成比例关系。拐点前其比例系数较小,摩擦力矩比较稳定;拐点后比例系数较大,摩擦力矩显著上升。当轴向载荷波动范围较大时,在摩擦力矩允许的范围内,适当减小轴向游隙可使拐点后移,获得更加稳定的摩擦力矩。
2)在低速区范围内,YRT转台轴承摩擦力矩随着转速的增大逐渐上升,但总体变化幅度较小;YRT转台轴承摩擦力矩随着轴向游隙的减小而逐渐上升,并且增幅逐渐增大。
3)滚子修形可有效降低YRT转台轴承摩擦力矩。相比于直线滚子和对数修形滚子,全凸圆弧修形可以更加有效地降低YRT转台轴承摩擦力矩。因此在YRT转台轴承的设计过程中,在满足轴承承载能力的条件下,应优先选用全凸圆弧修形滚子,以降低轴承的摩擦力矩。

