周向短弹簧型双质量飞轮参数匹配
(江苏大学汽车与交通工程学院, 江苏镇江212013)
0 引言
双质量飞轮式扭振减振器DMF是一种降低传动系扭转振动的新型扭振减振器[1-3]。双质量飞轮将原本位于离合器内部的扭振减振器布置到发动机的飞轮内部[2-3]。由于发动机飞轮的直径较大,使减振器的布置空间相应也增大很多,扭振弹簧的扭转刚度得以降低(扭转刚度只为离合器从动盘式扭转减振器的1/30~1/20),同时也增大了减振器工作时的扭转角度(极限转角能够达到30°~70°)[4-5]。这样布置扭振减振器使汽车怠速工况下的共振转速和行驶工况下的共振频率降低,因而能够发挥出更优良的减振性能[6]。自其诞生的20世纪80年代中期以来,逐渐的广泛运用于各类汽车[7-8]。现阶段,国外双质量飞轮的技术已经结构成熟、性能稳定,拥有成熟的产业结构链、大量的专利产品和相关研究论文,特别是欧洲市场双质量飞轮扭转减振器运用最为广泛[9]。但在国内,双质量飞轮的普及度不高,国内汽车零配部件生产商还处于试制研究阶段,汽车装配的双质量飞轮主要途径还是通过引进外企合资生产和外购直接获得[4]。相关领域的研究探索起步较晚,研究不够深入,在一些关键、核心零配件的制造工艺水平仍存在较大的技术难点,使国产双质量飞轮的性能与国外的同类产品性仍存在较大差距[10]。本文以一种具有五级刚度特性的双质量飞轮—周向短弹簧(dual mass flywheel-circumferential short spring, DMF-CSS)型扭振减振器为研究对象,对周向短弹簧型双质量飞轮扭振减振器的主要参数匹配分析和试验验证。
1 DMF-CSS的结构
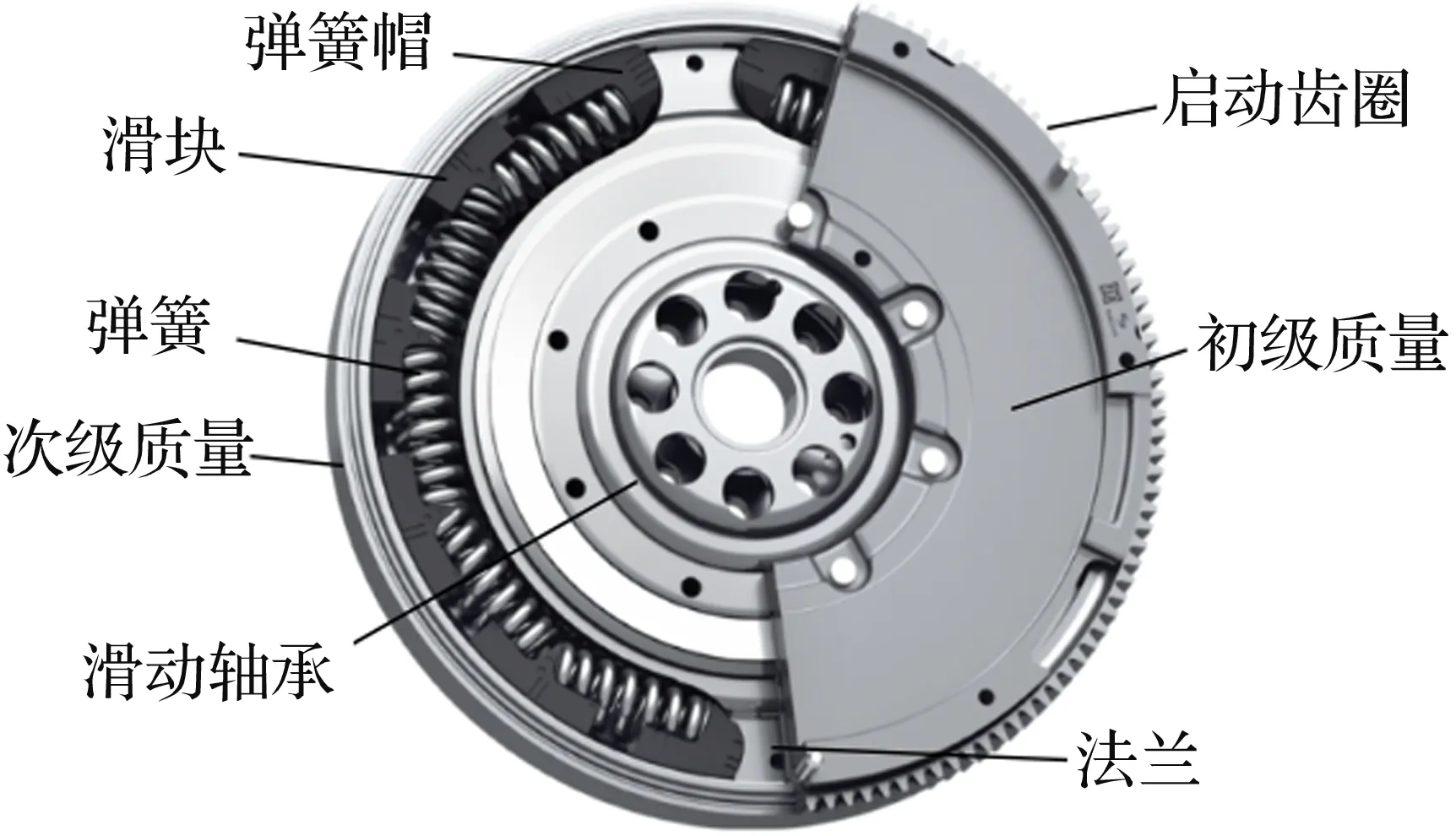
图1 DMF-CSS型扭振减振器结构Fig.1 Structure of DMF-CSS
DMF-CSS型扭振减振器的机械结构如图1所示。双质量飞轮将原发动机的飞轮顺轴向分为两个部分,第一部分布置在靠发动机一侧,与发动机的启动齿圈相结合,这部分也称为DMF的初级质量,第二部分与离合器相结合,这部分也称为DMF的次级质量。初级质量与次级质量之间设置有弹性机构和阻尼机构,两者通过弹性机构传递发动机的扭矩,实现相对转动,通过阻尼机构衰减由发动机端传递的扭矩波动,实现传动系统的扭振控制。
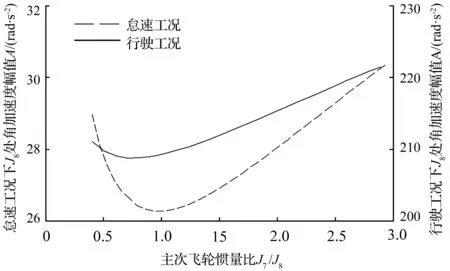
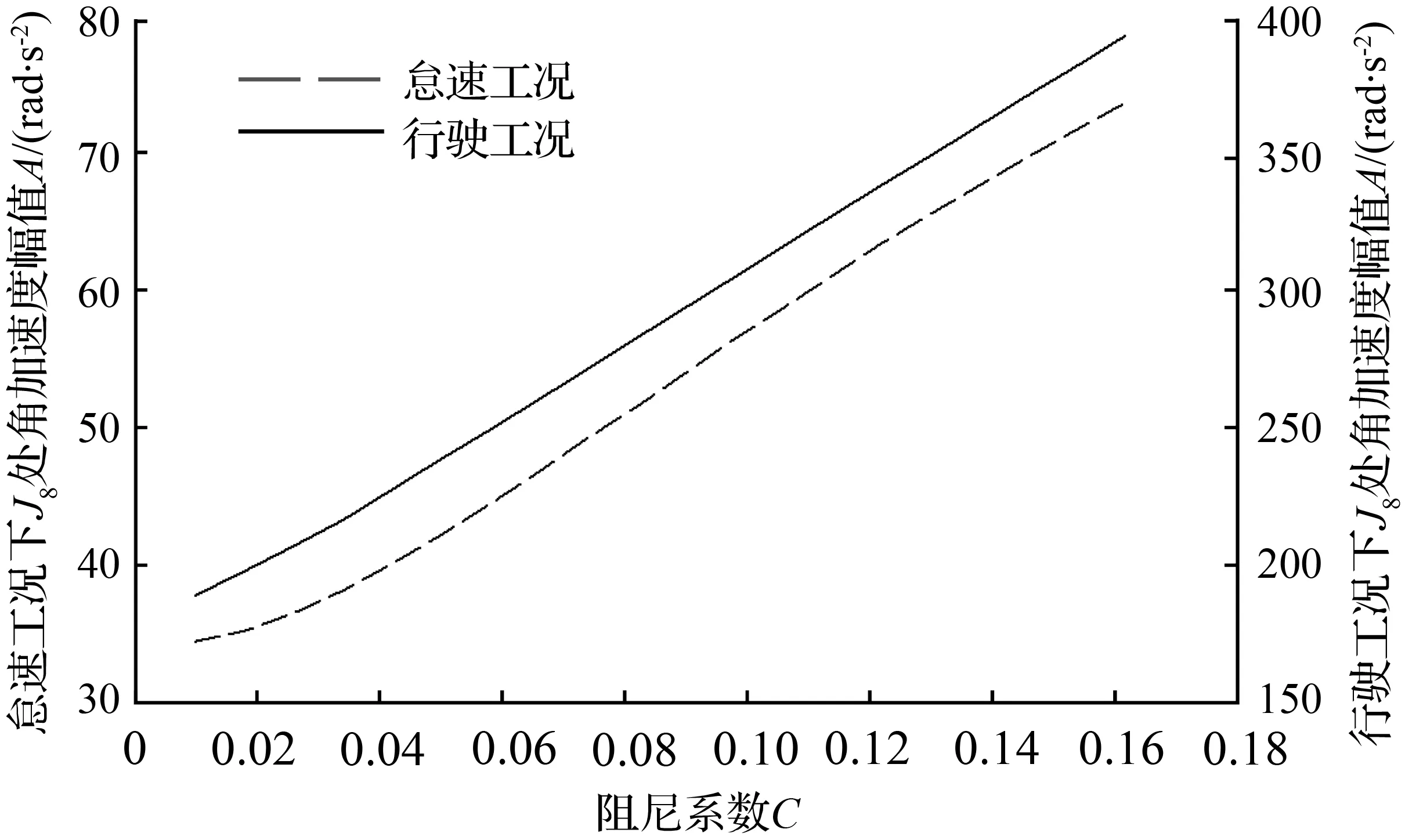
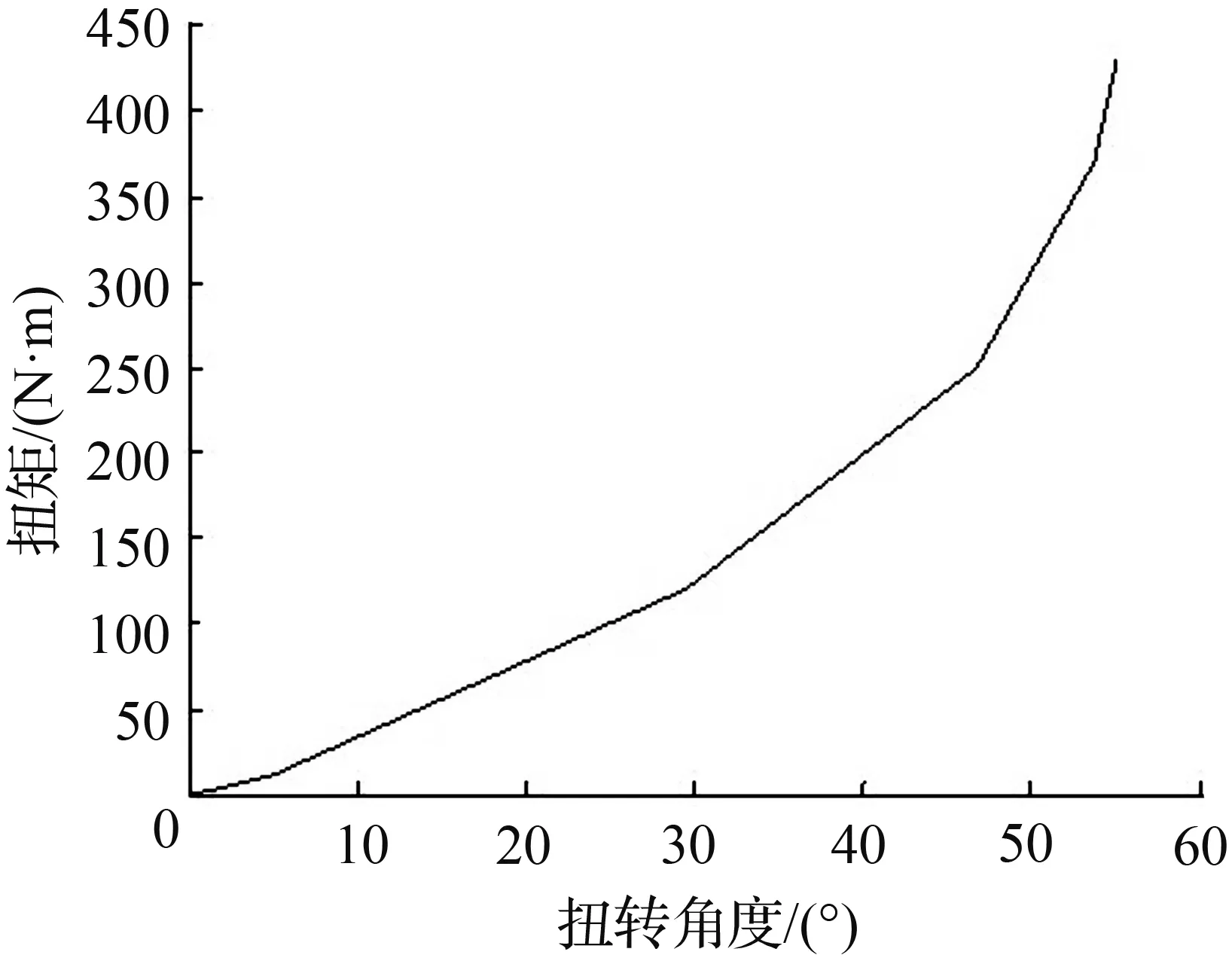
本文所讨论的双质量飞轮的弹性机构由2组弹簧组成,对称布置在初级质量和弹簧盖盘形成的两个弹簧腔内,并通过驱动盘将2组弹簧并联起来。每组弹簧的布置形式和结构参数相同,均由分布半径相同的5种刚度(K1 实际的汽车动力传动系统是一复杂的弹性体系,质量、刚度和阻尼是分析振动系统的三要素[11]。根据简化前后系统的动能和势能保持不变的原则来建立整车动力传动系统当量模型,并在MATLAB中对当量模型建模[12-13]。图2、图3分别为正常行驶与怠速停车工况下的整车动力传动系统简化模型。正常行驶工况下的传动系统扭振模型为11集中质量模型。怠速停车工况下,传动系统扭振模型为9集中质量模型。 图2 采用DMF的整车动力传动系行驶扭振模型 图3 采用DMF的整车动力传动系怠速扭振模型 模型中Ji为转动惯量;Ki为扭转刚度;Ci为阻尼系数。 根据前文建立的整车动力传动系统扭振模型将双质量飞轮扭振减振器的扭转刚度K、阻尼参数C以及 DMF初级惯量和次级惯量的比值J7/J8三个性能参数作为分析变量。对于评判参数,考虑到双质量飞轮扭振减振器的作用为衰减发动机输出扭矩的波动,因此以J8处角加速度幅值作为评判标准,分析双质量飞轮减振器参数对减振性能的影响[14-16]。 基于建立的怠速工况和行驶工况的动力传动系统扭振分析模型,进行仿真分析。以扭转刚度为设计变量,汽车稳定工况下J8处扭振角加速度幅值A为目标函数,进行仿真分析,可以得到角加速度幅值A与扭转刚度K的关系曲线如图4所示。 图4 角加速度幅值与扭转刚度的关系曲线Fig.4 Relationship between angular acceleration amplitude and torsion stiffness 由图4 可知,怠速工况时,J8处扭振角加速度幅值在设计变量约束条件内,随着扭振刚度的增加先增大后减小。这是由于随着刚度K的增加传动系统的固有频率逐渐接近怠速时的激振频率,从而产生共振振幅变大,当刚度增加到一定值后固有频率又开始远离激振频率,此时振幅开始下降。行驶工况时,角加速度幅值在设计变量约束条件内随着扭振刚度的增大而增大。因此在满足双质量飞轮传递极限转矩的前提下,扭转刚度K的值应该尽量取小,这样能够更好的避开共振的发生以及进行扭振控制。 基于建立的怠速工况和行驶工况的动力传动系统扭振分析模型,以J7/J8的比值为设计变量,汽车稳定工况下J8处扭振角加速度幅值A为目标函数进行仿真分析,可以得到角加速度幅值A与惯量比J7/J8的关系曲线如图5所示。 图5 角加速度幅值与转动惯量比的关系曲线Fig.5 Relationship between angular acceleration amplitude and moment of inertia ratio 从图5可以得出,怠速工况时,J8处扭振角加速度幅值在设计变量约束条件内,随着扭振刚度的增加先减小后增大,其中当J7/J8≈ 0.985时,加速度振幅A取最小值。行驶工况时,J8处扭振角加速度幅值在设计变量约束条件内,随着扭振刚度的增加大先减小后增大,其中当J7/J8≈ 0.764时,加速度振幅A取最小值。因此,对于所研究车型当惯量比J7/J8在0.764~0.985时,对于扭振控制较好。 采用以上相同方法,以阻尼系数C为设计变量,可以分析得到角加速度幅值A与阻尼系数C的关系曲线如图6所示。 图6 角加速度幅值与阻尼系数的关系曲线Fig.6 Relationship between angular acceleration amplitude and damping coefficient 由图6可知,怠速工况和行驶工况下,J8处扭振角加速度幅值在设计变量约束条件内,都随着阻尼系数C的增大而增大。根据机械振动原理,适当的阻尼有助于减少机械结构的共振振幅,使其快速恢复到稳定状态,但如果阻尼过大反而会增加振动的传递率。由于该传动系在匹配双质量飞轮扭振减振器后,使系统在怠速工况和发动机正常工作转速范围内不会产生严重的共振,在这种情况下如果阻尼过大反而会增加振动的传递率,不利于扭振的控制,同时又需要一定的阻尼去迅速衰减因冲击而产生的瞬态扭振。因此设计DMF阻尼系数C应尽量取偏小值。 图7 飞轮扭转角度和转矩的关系Fig.7 Relationship between the flywheel angle and torque 本文所讨论的周向短弹簧型扭振减振器的匹配对象是某款商用车型,其发动机的参数如下:四缸柴油发动机的最大扭矩为330 N·m,功率为136 kW,转速范围为800~6 000 r/min,最大功率转速3 800 r/min,最大扭矩转速1 800~2 800 r/min。结合设计要求:双质量飞轮能实现五级刚度的切换,其中第一级主要在发动机怠速时起作用,第二、三级主要在发动机正常驱动时起作用,第四级主要用于传递更大转矩时起作用,第五级主要在发动机极限扭矩输出时起作用。基于参数仿真模型,可以确定周向短弹簧型双质量飞轮的设计参数,如表1所示。根据其弹簧设计参数可以得到对应的转角与转矩的关系曲线如图7所示。 表1 飞轮设计参数Tab.1 Flywheel design parameters 为了验证设计的有效性,进行了双质量飞轮的实车试验。如图8所示,传感器分别装在发动机的启动齿圈处与变速箱的一轴常啮合齿轮上[17]。 通过试验得到汽车怠速、加速、正常行驶工况下初级飞轮和次级飞轮角加速度与时间的关系曲线图。图9~图11分别为整车怠速、加速和正常行驶工况的整车试验曲线,分析试验曲线得到以下结论。 汽车怠速工况时,DMF对发动机角加速度的衰减近71.4 %,效果显著。因此怠速时扭转刚度应尽量小,增加减振效果。 汽车行驶工况时,在加速过程的7~14 s内,DMF对发动机角加速度的衰减明显,最大衰减近78.6 %。在15~18 s时减振效果并不明显,是由于此时发动机突然减速,地面的冲击造成DMF反向扭转,瞬间经历三次刚度突变,因而减振效果不明显。25~30 s时,在阻尼的作用下振动迅速衰减然后达到稳定状态。 综上所述,为了更有效的衰减发动机怠速工况时的振动需要在设计时使扭振弹簧刚度尽量小,合适的阻尼比有利于快速的衰减振动,同时在设计多级扭转弹簧刚度双质量飞轮时需要考虑不同刚度级间的刚度突变问题。 图8 传感器装配位置 图9 双质量飞轮怠速试验 图10 双质量飞轮加速试验 图11 双质量飞轮行驶试验 本文在分析了周向短弹簧型双质量飞轮的结构特点基础上,建立了装有周向短弹簧型双质量飞轮的车辆动力传动系统分析模型。以一种具有五级式非线性弹性特性的周向短弹簧型双质量飞轮为研究对象,分析了双质量飞轮主要性能参数对其减振性能的影响。以某商用车为研究对象,设计了与其传动系统参数匹配的双质量飞轮,通过样件进行了整车试验验证。试验结果表明,根据前文设计理论所设计的周向短弹簧型双质量飞轮具有良好的减振性能。通过本文研究,可以得到以下结论:双质量飞轮传递极限转矩、极限转矩的前提下,扭转刚度K的值应该尽量取小;初级惯量和次级惯量的比值J7/J8应根据传动系统参数取合适值;阻尼系数C的值应尽量取小。2 装有DMF-CSS车辆动力传动系统扭振模型
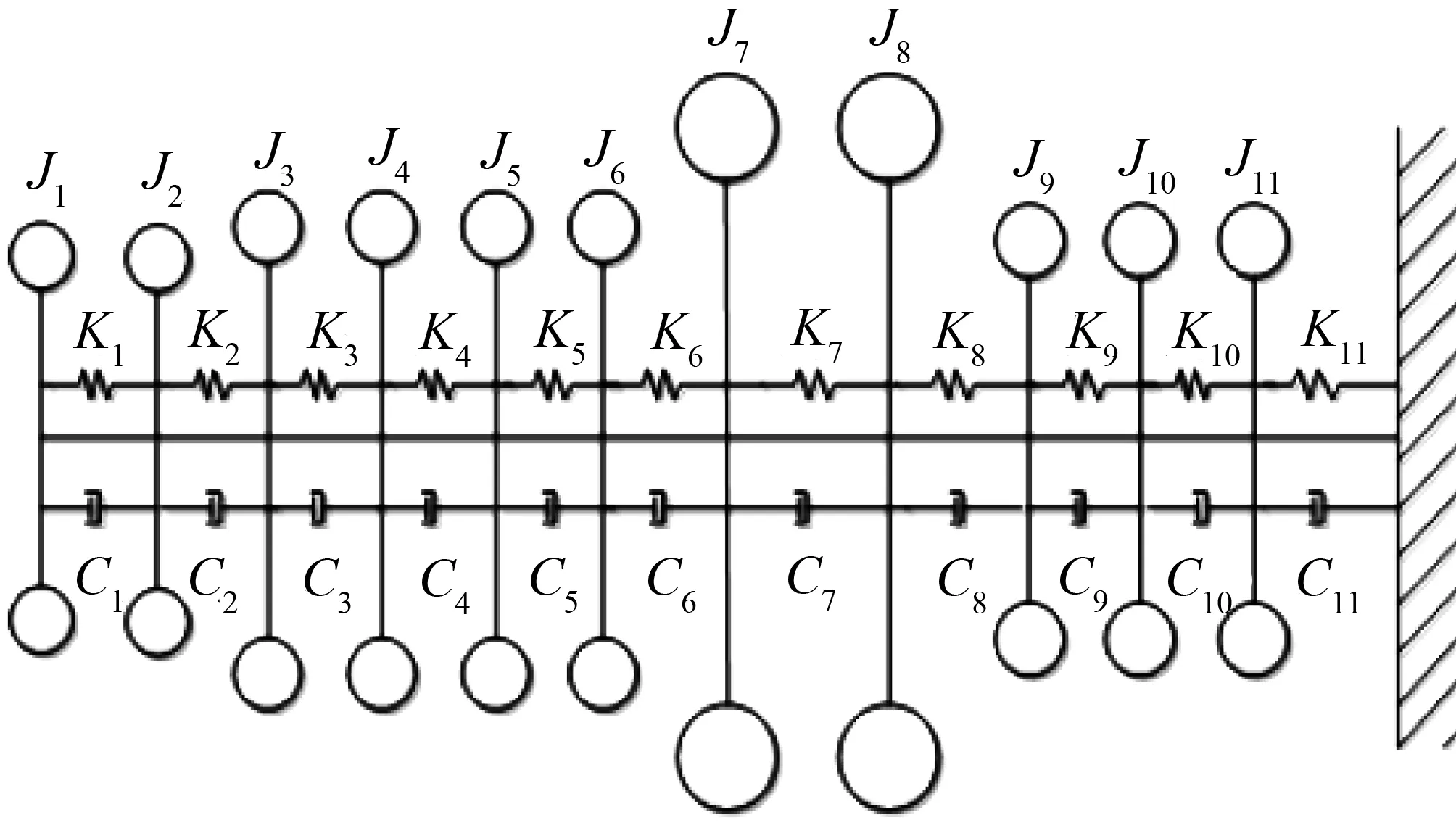
Fig.2 Torsional vibration driving model of vehicle’spower transmission system with DMF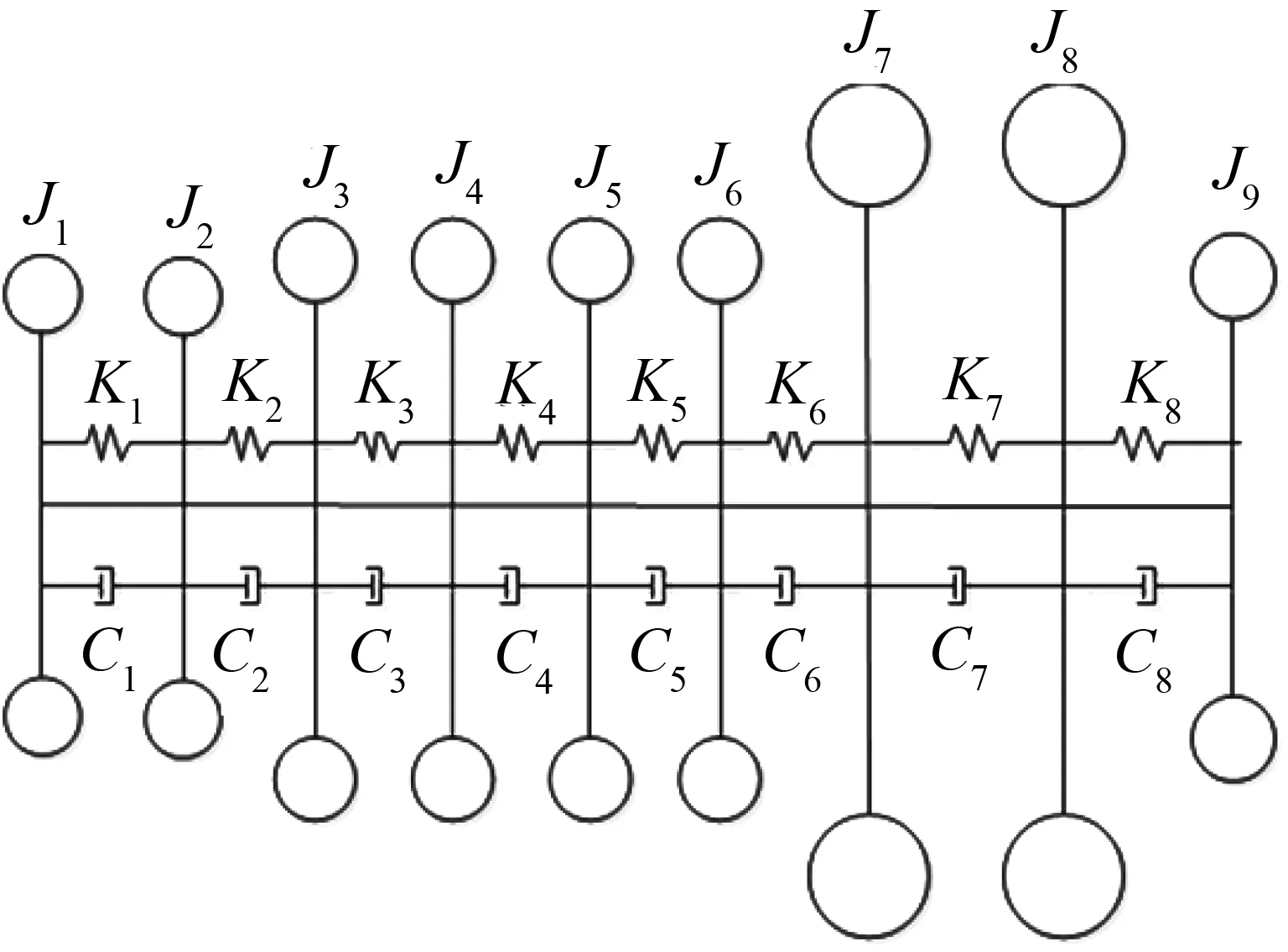
Fig.3 Torsional vibration idle speed model ofvehicle’s power transmission system with DMF3 双质量飞轮减振器参数对减振性能影响分析
3.1 扭转刚度对减振性能的影响
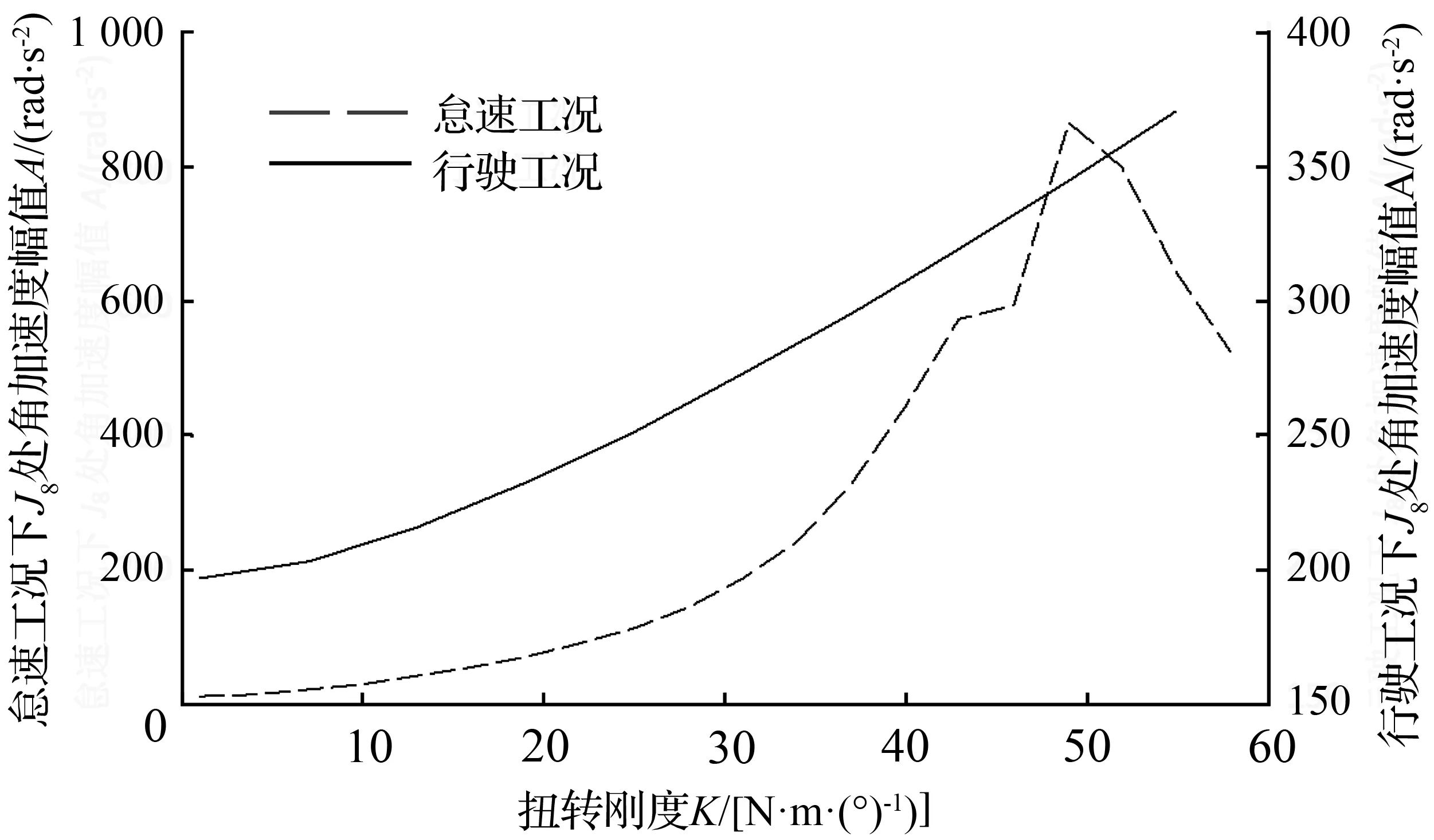
3.2 惯量比对减振性能的影响
3.3 阻尼比对减振性能的影响
4 DMF-CSS参数设计与整车试验
4.1 DMF-CSS的参数设计

4.2 DMF-CSS的整车试验

Fig.8 Sensor assembly location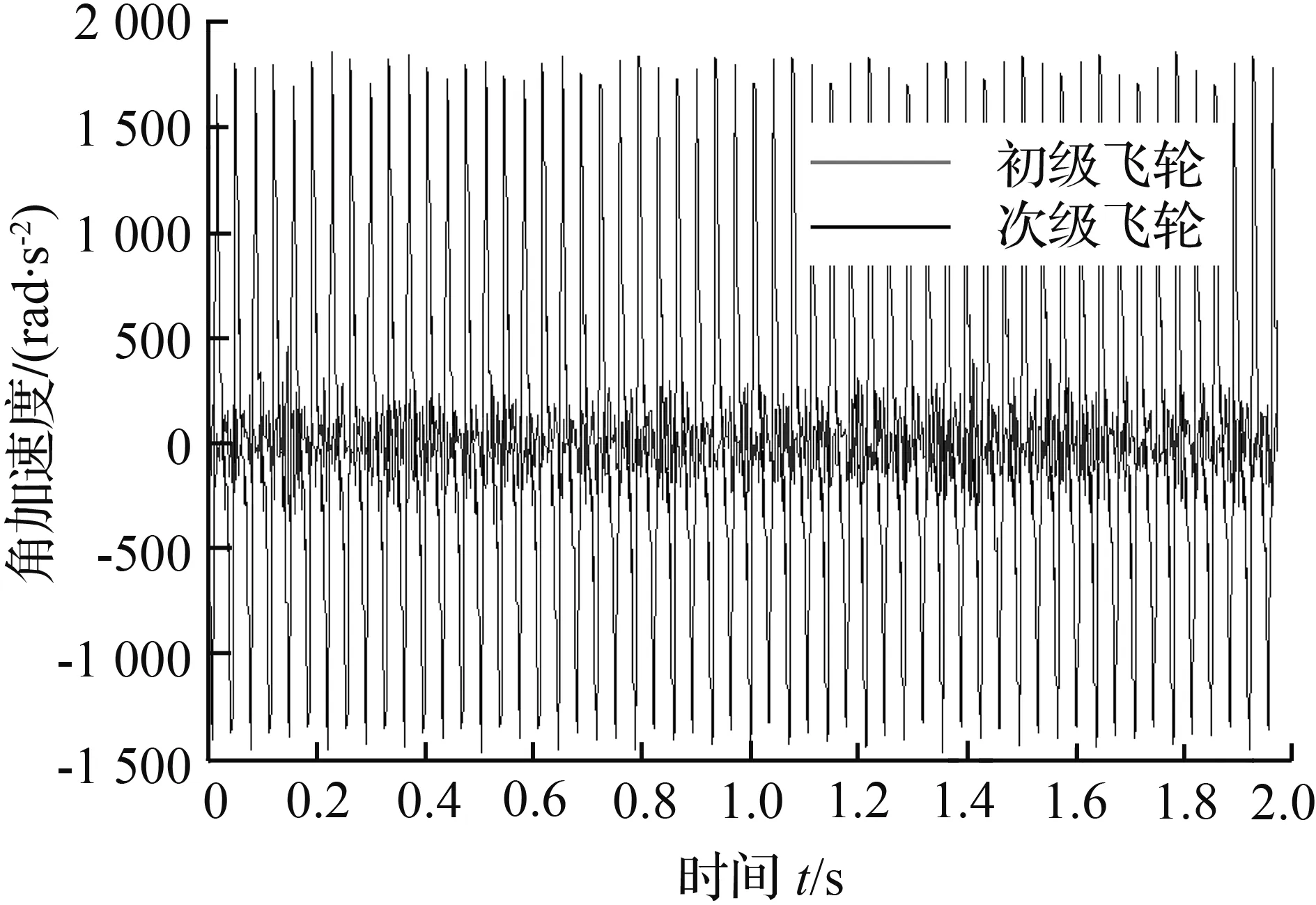
Fig.9 Dual-mass flywheel idle speed experiment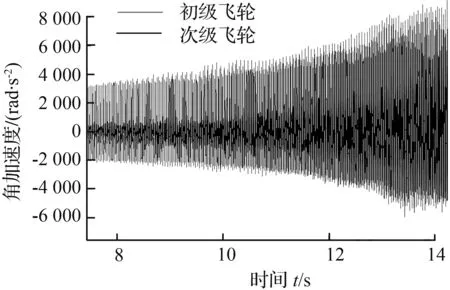
Fig.10 Dual-mass flywheel accelerated experiment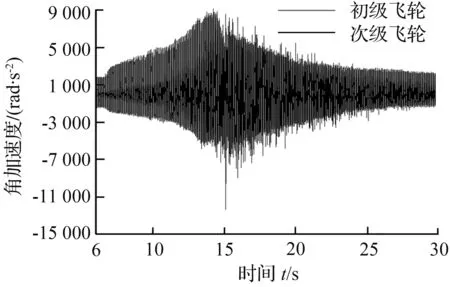
Fig.11 Dual-mass flywheel driving experiment5 结论

