一种可控机构式码垛机器人的间隙误差补偿

唐俊杰，晏紫琦，徐敬彭，蔡敢为

(广西大学机械工程学院， 广西南宁530004)

0 引言

由于加工误差、装配不合理以及实际工作中磨损等因素的客观存在，运动副间隙对精度的影响不容忽视。近年来，国内外学者致力于研究运动副间隙对机构精度的影响。在间隙误差分析方面，Venanzi等[1]采用虚功原理对运动副间隙误差进行分析；Tsai等[2]在此基础上研究了运动副间隙对机械传动的影响；张义民等[3]结合虚功原理和优化技术，提出一种分析平面机构误差的数值计算方法。在间隙误差补偿方面，沈江等[4]采用加逆模前馈的PID控制对含间隙曲柄滑块机构进行误差补偿；张宪民等[5]对3-RRR并联机器人进行误差标定进而在机构逆运动学中进行识别补偿；谢平等[6]以及余跃庆等[7]均通过优化算法对并联机器人进行优化补偿。以上研究均能较好的提高机器人的定位精度，但是在研究过程中，较少考虑运动副间隙误差产生的原因和变化的规律，同时也未能将所研究的理论运用于工程实践。

传统串联式码垛机器人需将旋转电机安装在关节处，不仅会增大机械臂的转动惯量，积累关节误差，还会导致末端执行器发生振动，严重影响工作精度[8]。本文基于串联式机器人的局限性，将可控式机构[9]和并联机构的理念融合，以增大承载能力、提高工作精度为目的[10]，设计出一种可控式码垛机器人，根据码垛机器人实际工况，选择两处受力变换频繁的关节采用连续接触模型[11]对运动副间隙引起的精度误差进行分析，利用改进的粒子群算法优化驱动杆位移参数，进而达到误差补偿的目的。

1 新型可控码垛机器人机构设计

本文所设计的码垛机器人底座与地面固定，由电机驱动旋转机架绕底座法向方向转动，其中大臂2的转角由电推缸4控制，小臂3的转角由电推缸4、6耦合控制。机架1、大臂2、平衡杆5和三角架7以及小臂3、三角架7、平衡杆8和平动保持架9组成两个平行四边形结构，用以增加机构稳定性、提高承载能力和保持输出末端水平。装夹电机安装在末端执行装置上，主要用于控制抓手的闭合与张开。码垛机器人的机构简图如图1所示。

将码垛机器人除旋转机架和末端执行装置以外的部分视为其主构型，则主构型是由四个互有联系的基本模块组成。其中大臂升降模块L1是由机架1、大臂2和电推缸4组成，通过调控电推缸4的伸缩长度进而控制大臂2旋转的角度；小臂调整模块L2是由大臂2、小臂3和电推缸6组成，小臂3旋转的角度是由大臂2的旋转角度以及电推缸6的伸缩长度联合控制；模块L3、L4均为平行四边形结构，码垛机器人的环路模块示意图如图2所示。

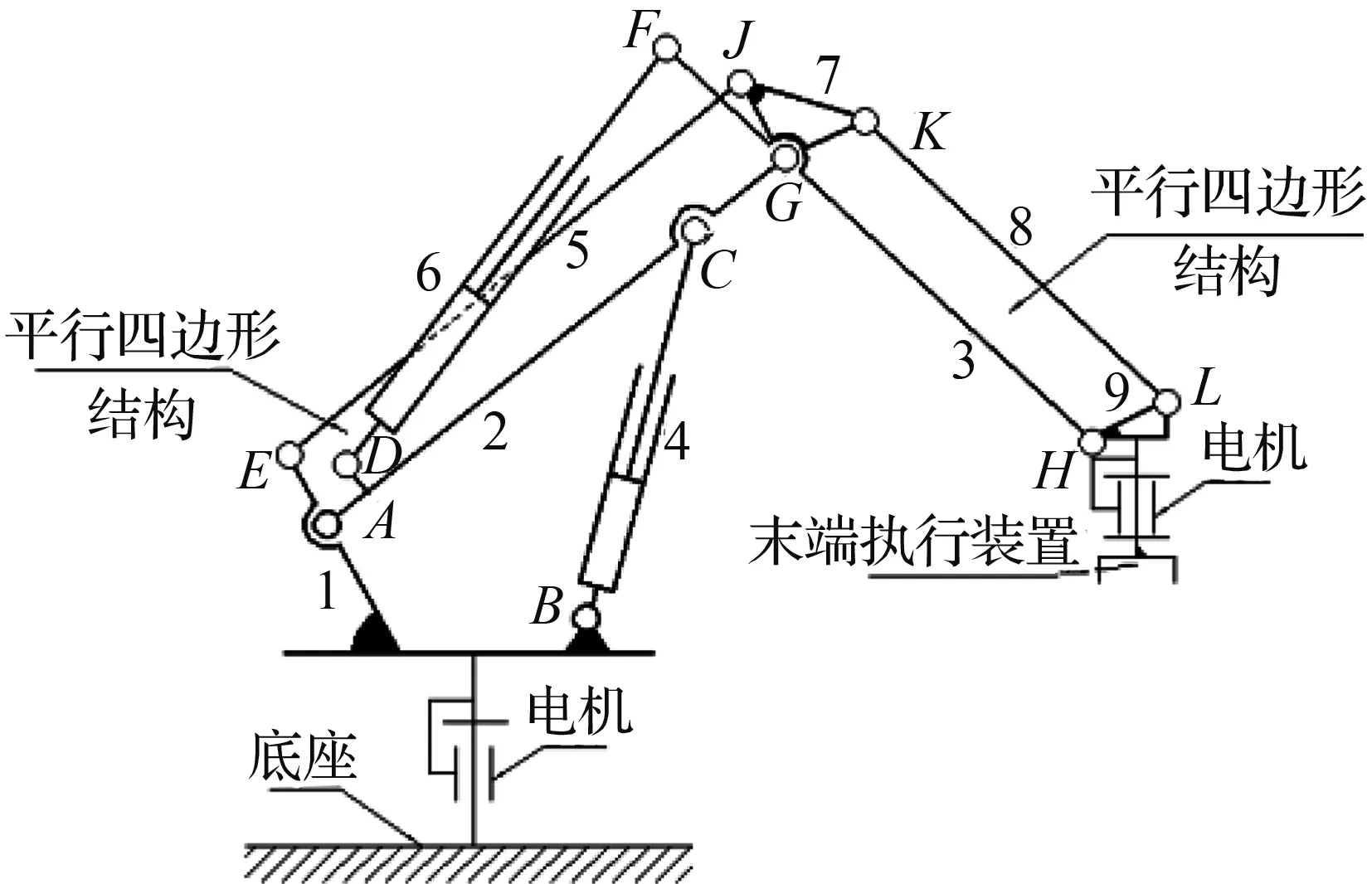
图1 码垛机器人机构简图
Fig.1 Schematic diagram of palletizing robot

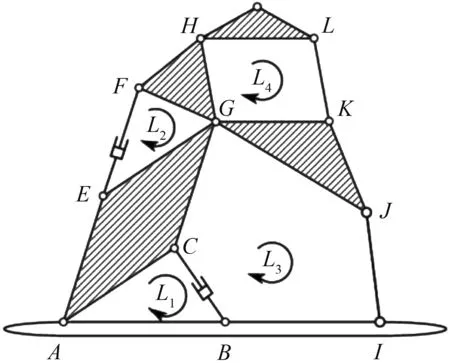
图2 码垛机器人环路模块图
Fig.2 Modular diagram of palletizing robot

2 考虑运动副间隙的误差分析

可控码垛机器人采用转动副实现运动传递和能量转换，但受限于加工制造、装配精度以及长期工作加剧运动副磨损等因素的影响，不可避免会存在运动副间隙。本文所设计的新型码垛机器人在工作过程中，C、F处杆端力的大小和方向变化频繁，需着重考虑这两处的转动副间隙对机构运动精度的影响。

图3 运动副间隙模型Fig.3 Model of joint clearance

建立如图3所示的运动副间隙模型。设转动副的孔和轴均为标准圆，半径分别是RB和RJ，在不考虑间隙时，杆件a的理想长度为l，理想角位移为θ；考虑运动副间隙时，杆件a的实际长度为l′，实际角位移为θ′。其中r是O到O′之间的长度，表示为误差圆的半径。杆长和角位移的变化引起系统的结构误差，进而使得末端偏离理想位置，根据图中所示，理想状况下的杆长和转角以及实际状况下的杆长和转角之间存在如下关系：

(1)

(2)

根据本文所研究的可控码垛机器人的实际工作轨迹，可将运动副间隙模型视为连续接触模型，视运动副间隙为一定长无质量的连杆。根据误差模型可知：

r=RB-RJ，

(3)

φ∈[0,2π]。

(4)

根据前文所划分的模块，以大臂升降模块(记为模块Ⅰ)和小臂调整模块(记为模块Ⅱ)为基础，分别对理想模型和考虑运动副间隙的实际模型进行分析，推导理论轨迹和实际轨迹之间的偏差。

在理想状态下(图4)，记lBC长度为l1，大臂旋转角度和电推缸4的旋转角度分别为φ1和φ2；考虑运动副间隙时(图5)，记lBC长度为l1′，其中l1′=l1+Δl1，大臂旋转角度和电推缸4的旋转角度分别为φ1′和φ2′，则有：

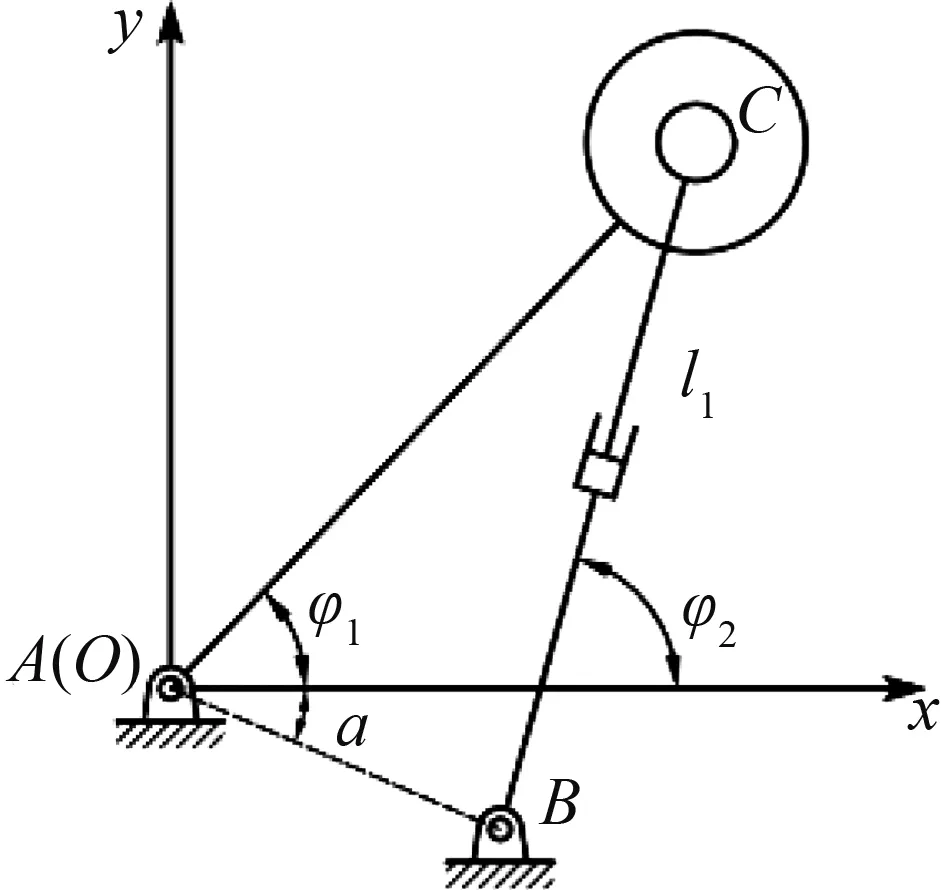
图4 理想状态下的模块Ⅰ
Fig.4 Modular Ⅰ without clearance

图5 含间隙状态下的模块Ⅰ
Fig.5 Modular Ⅰ with clearance

(5)

(6)

(7)

(8)

在该运动副间隙模型下销轴与套筒内壁连续接触，则lCC′的长度为定值，表示为：

((l1+Δl1)cosφ2′-l1cosφ2)2+((l1+Δl1)sinφ2′-l1sinφ2)2=(RB-RJ)2，

(9)

其中：

RJ-RB≤Δl1≤RB-RJ。

(10)

在理想状态下(图6)，记lEF长度为l2，小臂旋转角度和电推缸5的旋转角度分别为φ4和φ3；考虑运动副间隙时(图7)，lEF长度为l2′，其中l2′=l2+Δl2，小臂旋转角度和电推缸5的旋转角度分别为φ4″和φ3″，则有：

图6 理想状态下的模块Ⅱ
Fig.6 Modular Ⅱ without clearance

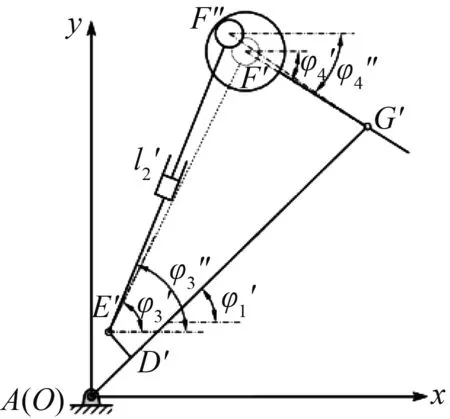
图7 实际状态下的模块Ⅱ
Fig.7 Modular Ⅱ with clearance

(11)

(12)

(13)

(14)

考虑到在连续接触模型[10]下销轴与套筒内壁始终接触，则lF′F″的长度为定值，表示为：

((l2+Δl2)cos(φ3″+Δφ1)-l2cos(φ3′+Δφ1))2+

((l2+Δl2)sin(φ3″+Δφ1)-l2sin(φ3′+Δφ1))2=(RB-RJ)2，

(15)

其中：

RJ-RB≤Δl2≤RB-RJ，

(16)

Δφ1=φ1′-φ1。

(17)

由码垛机器人机构简图可知，H点与平动保持架相连。本文选取平动保持架的中点位置为参考点，对由运动副间隙引起的结构误差进行分析，该点的轨迹(x,y)表示为：

(18)

其中d表示为水平方向上H点与参考点之间的距离。

理想状态下，参考点的轨迹表示为：

(19)

考虑运动副间隙的状态下，参考点的轨迹表示为：

(20)

记Δx=x′-x、Δy=y′-y，分别表示某一时刻理想轨迹与实际轨迹在x、y方向上的差值。

3 改进的PSO算法

粒子群算法是基于生物种群行为实现优化的一种智能算法。使用粒子群算法进行优化，需初始化若干无质量无体积的粒子，将每个粒子视为一个优化的可行性方案，通过设定区间以保证粒子的运动范围，设定适应度函数判定粒子的优劣[12]。通过模拟生物种群行为，粒子将通过继承先前运动、思考下一步决策以及与其他粒子共享信息等方法追随当前最优粒子，逐步迭代进而得到最优解。每次迭代过程中，粒子均跟随自身找寻到的最优解以及种群找寻到最优解两个极值。因而该算法无交叉、变异运算，搜索速度快，结构简单，优化效果较好。但由于未能对速度进行动态调节，容易陷入局部寻优而降低收敛精度，此外需要考虑参数控制来实现最优效果。

标准PSO算法表示为：

(21)

其中ω为惯性因子，用以确定搜索类型：若ω取较大值，适用于全局寻优，若ω取较小值，有利于局部搜索；c1、c2为学习因子且二者均大于零，反映为粒子群间的信息共享与交流；xij、vij分别表示为粒子i的位置和速度；pij、pgj分别为粒子i的个体最优位置和群体最优位置；r1、r2分别为分布于[0,1]之间的随机数。

针对上文所分析粒子群算法的不足，本文引进线性递减的权重因子，以实现在迭代初期加强全局寻优，在迭代后期专注局部寻优的效果，进而规避其容易陷入局部寻优，导致精度差的缺点。

(22)

其中ωs、ωf分别为起始、终止时刻的惯性因子，tmax为最大迭代步数。

在进行计算时，每个粒子均需要重新完成完整的PSO算法寻优，计算周期长，优化周期多，优化过程中粒子陷入局部最优的概率也随之增大。因此，为提高计算效率，提升求解精度，此处引入压缩因子γ[13]，代入式(21)中可得：

vij(t+1)=γ·[ωvij(t)+c1r1[pij(t)-xij(t)]+c2r2[pgj(t)-xij(t)]]，

(23)

其中：

(24)

根据以上分析，本文引入一种标准PSO算法和三种改进的PSO算法进行迭代计算，四种算法的各项参数如表1所示：

表1 PSO优化算法参数Tab.1 Parameters of PSO algorithms

4 基于PSO算法的误差补偿

本节基于前文所分析的精度误差，利用改进的PSO算法对可控码垛机器人由运动副间隙所引起的误差进行补偿。根据式(5)～式(20)，定义末端参考点的位移偏差为适应度函数：

(25)

可控码垛机器人结构参数如表2所示：

表2 可控码垛机器人机构参数1Tab.2 Mechanical parameters table of palletizing robot

注1：lABx、lABy分别为lAB在x、y方向上投影的长度。

参考点的位姿误差是由机构名义结构误差、驱动杆输出误差以及运动副间隙误差所引起的实际结构误差共同作用，是一个多输入、多变量、强耦合的非线性方程，因此很难通过解析计算求得最优解，故将其转换为优化问题。定义dli=Δli+δli，其中δli称为驱动杆位移参数，本节对δli进行优化，通过减小Δφ1′和Δφ4″，达到补偿间隙误差的目的。

本文所研究的主构型是由电推缸4、6进行驱动，可视其长度为变量。因此定义驱动函数为：

(26)

将式(26)代入式(5)～式(25)中，运动副间隙补偿的流程如下：

图8 位姿误差适应度曲线Fig.8 Fitness curves of position error

①根据前文分析的间隙误差模型，确定理论轨迹、理论结构参数以及考虑运动副间隙的误差结构参数；

②将理论轨迹、理论结构参数和误差结构参数代入到粒子群优化算法中，通过迭代降低适应度值直至满足终止条件；

③将优化后的驱动函数输入到模型中，计算出实时末端实际轨迹；

④重复①～③，最终完成误差补偿。

根据以上分析，绘制位姿误差随迭代次数增加而变化的适应度曲线如图8所示：

由图8所示，两种压缩因子的粒子群算法收敛速度较快，递减权重压缩因子的粒子群算法收敛性能最佳，本文利用该算法对运动副间隙引起的误差进行补偿。

以递减权重压缩因子的粒子群算法进行优化时，绘制的x，y方向参考点轨迹曲线对比图。

图9x方向轨迹曲线对比图
Fig.9 Comparison of trajectorycurves along thex-axis

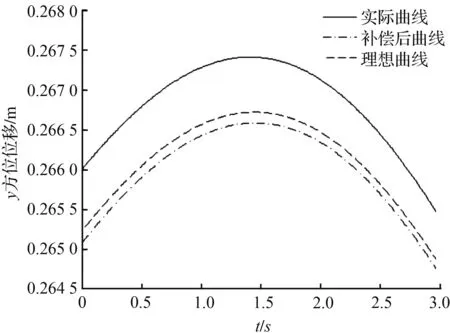
图10y方向轨迹曲线对比图
Fig.10 Comparison of trajectorycurves along they-axis

利用MATLAB编程对曲线数据进行处理，结果如表3所示：

表3 误差补偿表Tab.3 Error compensation table

由表3可知，设定初始位置Δl1=Δl2=0.000 1 m，采用递减权重压缩因子的粒子群算法对驱动杆位移参数进行优化，x轴方向补偿率为90.27 %，y轴方向补偿率为80.45 %，能达到较好的优化效果。采用该方法再加上控制系统调控，可降低由运动副间隙所引起的位姿误差，有效地提高了机构精度可靠性。

5 结语

本文将可控式机构与并联机构的理念结合，以提高承载能力和工作精度为目的，设计出一种新型可控式码垛机器人，以该机器人的主结构为研究对象，建立运动副误差模型。分析由运动副间隙引起的结构误差，结合码垛机器人实际工况，选取两处杆端力大小和方向变化频繁的关节，视其孔轴之间为一定长无质量连杆进行优化分析。分别对理想模型和含间隙模型进行计算，推导其末端参考点沿x、y轴方向的轨迹方程，二者相减即为轨迹误差。对该误差进行优化，通过递减权重和压缩因子两种方法对标准PSO算法进行改进，以达到降低适应度值的效果。利用文中改进的PSO算法优化驱动杆位移参数，设定初始位置进行仿真，通过仿真迭代可得，在x轴方向的补偿率达到90.27 %，在y轴方向的补偿率达到80.45 %，结果表明采用该方法可降低由运动副间隙引起的结构误差，进而有效地提高工作精度和效率。