道路损伤系数解析式及影响规律分析

(1.山东理工大学交通与车辆工程学院， 山东淄博255049;2.徐州徐工随车起重机有限公司， 江苏徐州221000)

公路运输是货物运输的重要方式之一。随着社会经济的发展，作为经济动脉的各级道路受到了不同程度的破坏，逐渐引起了人们的关注[1]。

造成道路破坏的原因很多，其中，车辆与道路之间的动态相互作用是重要原因之一[2-3]。车辆超载使得路面出现不同方向的裂缝、凹陷，随机的轮载作用又加速了路面的疲劳破坏[4-5]。为了探究车辆和道路之间的作用机理并降低车辆对路面的损坏，学者们进行了有益的探索。文献[6]提出了路面平整度劣化模型并基于此进行了劣化规律分析；文献[7]研究表明车辆行驶速度对路面破坏有一定的影响;文献[8]分析了道路在轮胎动载长期作用下的损伤;Melzi等利用数值方法分析了轮胎特性及土壤响应等对农用车舒适性的影响[9];Erlingsson分析了路面在重型卡车作用下的路面响应特性[10];Li等研究表明轮胎动载对路面沥青层的破坏具有重要影响[11]。这些研究对探明车辆对道路损伤的影响提供了有益参考，但对于车辆对路面损伤程度的量化评价指标还有待深入研究。尽管文献[12]提出了沥青路面多种破坏的统一力学指标，但理论分析较为复杂，不便于一般的工程技术人员掌握和应用。为了有效地量化评价路面损伤程度且便于工程应用，还需要简洁、可靠的量化指标解析计算方法。

本文建立了车—路系统动力学模型;根据道路损伤系数的定义，推导道路损伤系数解析式。以某车为例，基于解析式揭示车辆参数对道路损伤的影响规律。

1 道路损伤系数的定义

传统上，常采用车辆的车轮动载荷来量化评价车辆对路面的损伤程度。车辆行驶时的车轮动载荷越大，对道路的破坏作用越大;车轮动载荷越小，道路友好性越好[13]。事实上，在路面随机激励下，车辆的振动是一个随机振动过程，车轮动载荷是一个随机量。因此，在实际评价分析时，一般采用车轮动载荷的标准差。现有实验研究与理论分析表明，道路损伤程度正比于路面所受车辆静载荷的4次幂。为了有效量化评价车辆对路面的损伤程度，将道路损伤系数p定义为[14]：

(1)

式中，σ为车轮动载荷的标准差，G为车辆的静载荷;p值越大表示车辆对道路的破坏性越大。

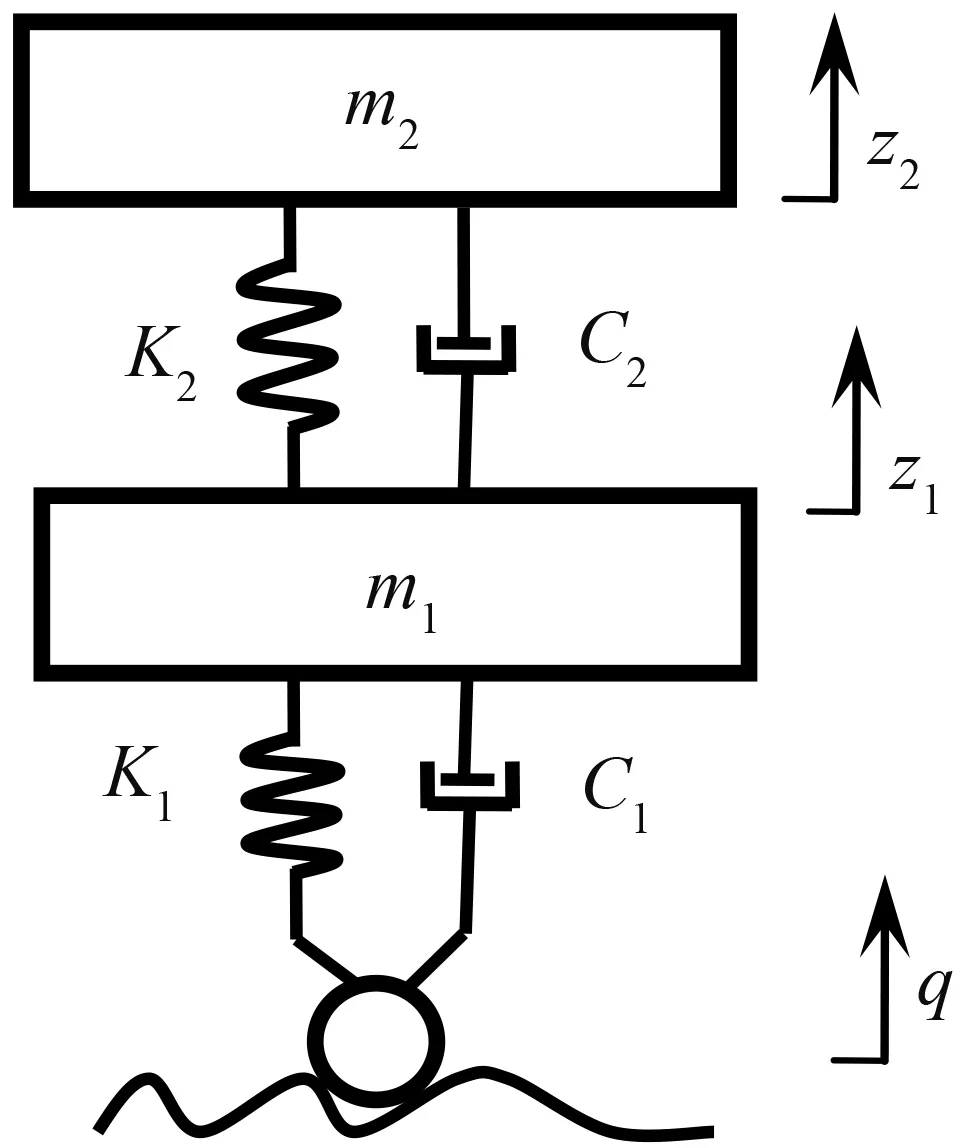
图1 二自由度车—路系统动力学模型Fig.1 Dynamic model of vehicle-road system with two degrees of freedom

2 道路损伤系数解析计算方法

2.1 车—路系统动力学模型

为了便于推导得出简洁、实用的道路损伤系数解析计算式，采用了二自由度车—路系统动力学模型，如图1所示。

在图1中，m1和m2分别表示车辆的簧下质量和簧上质量;K1和K2分别表示轮胎的垂向刚度和悬架系统垂向刚度;C1和C2分别表示轮胎的垂向阻尼和悬架系统垂向阻尼;z1和z2分别表示轮胎系统的垂向跳动量和车身的垂向位移;q为路面的垂向激励位移。

由于轮胎阻尼C1很小，常忽略不计[15]。因此，根据牛顿第二定律，可得系统振动微分方程为：

(2)

2.2 道路损伤系数解析计算式

根据汽车理论，车轮动载荷可表示为：

Fd=K1(z1-q)。

(3)

(4)

式中，s为拉式变换算子，Q和Z1分别表示q和z1的拉式变换形式。

根据系统的振动微分方程(2)，可将式(4)进一步表示为：

(5)

式中，A0=K1K2，A1=K1C2，A2=K1m2+K2m1+K2m2，A3=C2m1+C2m2，A4=m1m2;B1=-(K1K2m1+K1K2m2)，B2=-(K1C2m1+K1C2m2)，B3=-K1m1m2;s=ωj，ω为路面激励圆频率，j为虚数单位。

车轮动载Fd的功率谱密度可表示为：

(6)

随机路面的速度功率谱密度可表示为：

(7)

式中，n0为参考空间频率，n0=0.1m-1，Gq(n0)为路面功率谱密度，v为车速。

将式(7)代入式(6)，可得：

(8)

根据式(8)，可将车轮动载Fd的标准差σ表示为：

(9)

根据车—路系统动力学模型，可将车辆的静载荷表示为：

G=(m1+m2)g，

(10)

式中，g为重力加速度，且g=9.8 m/s2。

将式(9)和式(10)代入道路损伤系数p的定义式(1)，可得:

(11)

将式(5)代入式(11)，并利用留数定理[16]，进行积分运算，可得道路损伤系数p的解析计算式为:

(12)

式中，

(13)

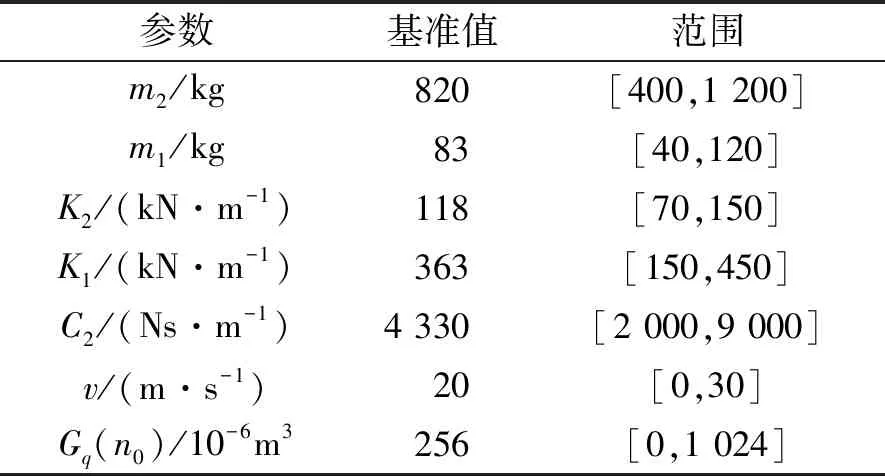
表1 车辆动力学参数值Tab.1 Value of vehicle dynamic parameters

3 影响规律分析

根据式(12)可知，道路损伤系数p与车辆行驶速度v、路面功率谱密度Gq(n0)及车辆参数有关。因此，下面基于式(12)计算并分析上述因素对道路损伤系数p的影响规律。在分析时，采用的某微卡车辆动力学参数基准值及参数取值范围如表1所示。

3.1 车辆参数对道路损伤系数的影响

图2所示为道路损伤系数p随车辆参数的变化曲线。图2(a)表明，随着簧上质量m2的增大，道路损伤系数p呈现强非线性增大，由此可见，车辆若超载则对路面的损伤程度将急剧增加。图2(b)表明，道路损伤系数p随簧下质量的增大而线性增大，由此可知，轮胎的轻量化有助于降低车辆对路面造成的损伤。

由图2(c)和图2(d)可知，随着悬架刚度K2及轮胎垂向刚度K1的增大，道路损伤系数p均呈现弱非线性增大，故采用较软的轮胎和悬架有利于提高车辆的道路友好性;由于在相同的额定载荷下，空气弹簧悬架的刚度明显低于钢板弹簧悬架的刚度，因此，配置空气弹簧悬架的车辆具有更好的道路友好性。图2(e)表明，道路损伤系数p随悬架阻尼的增大，先减小后增大，存在最优值使得p最小化。因此，可通过优化匹配悬架系统减振器，降低车辆对道路造成的损伤。

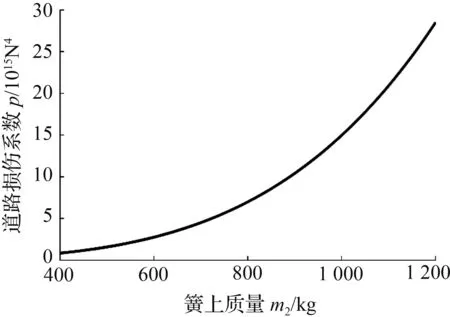
(a) 道路损伤系数p随簧上质量m2的变化曲线

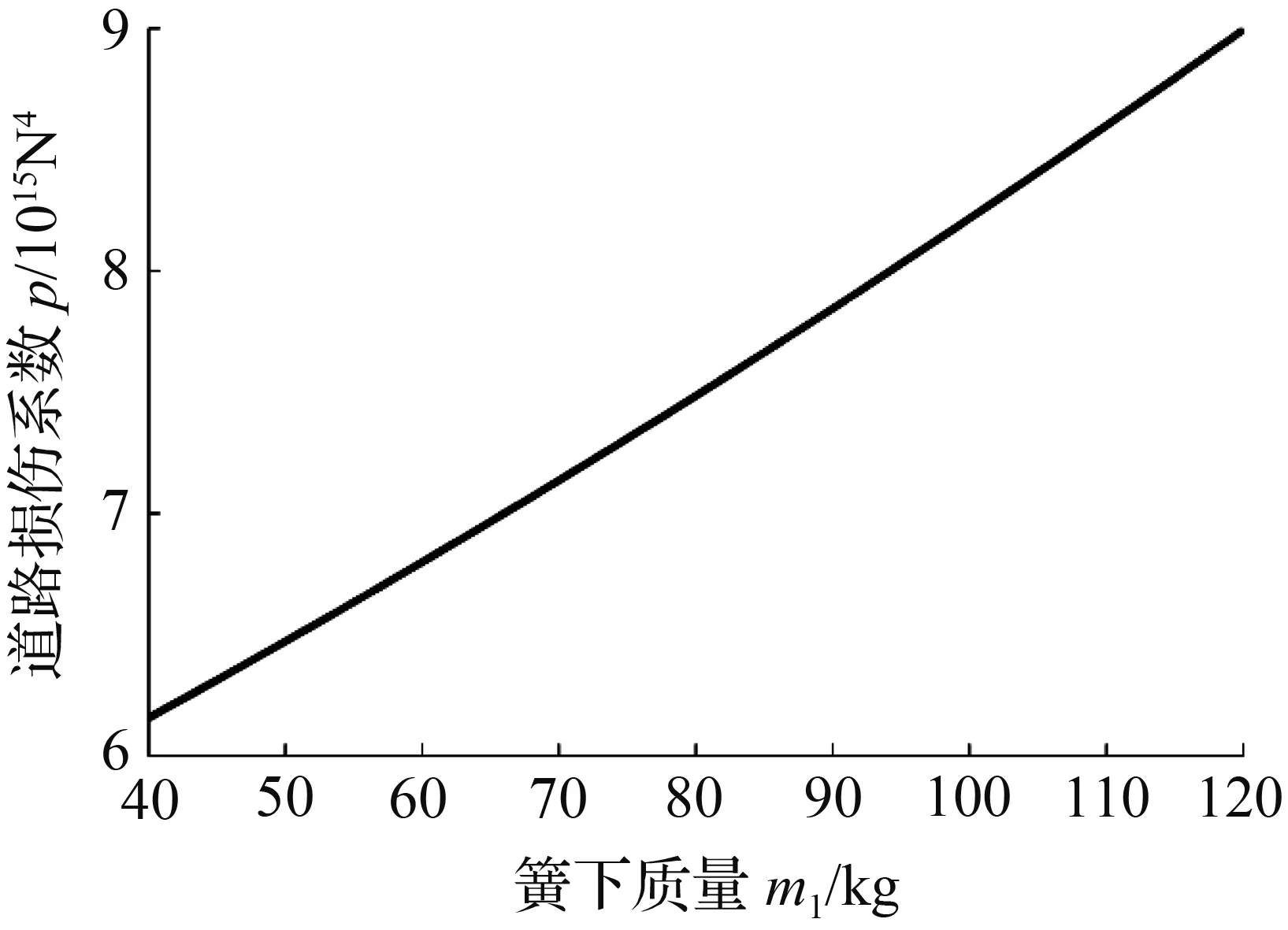
(b) 道路损伤系数p随簧下质量m1的变化曲线

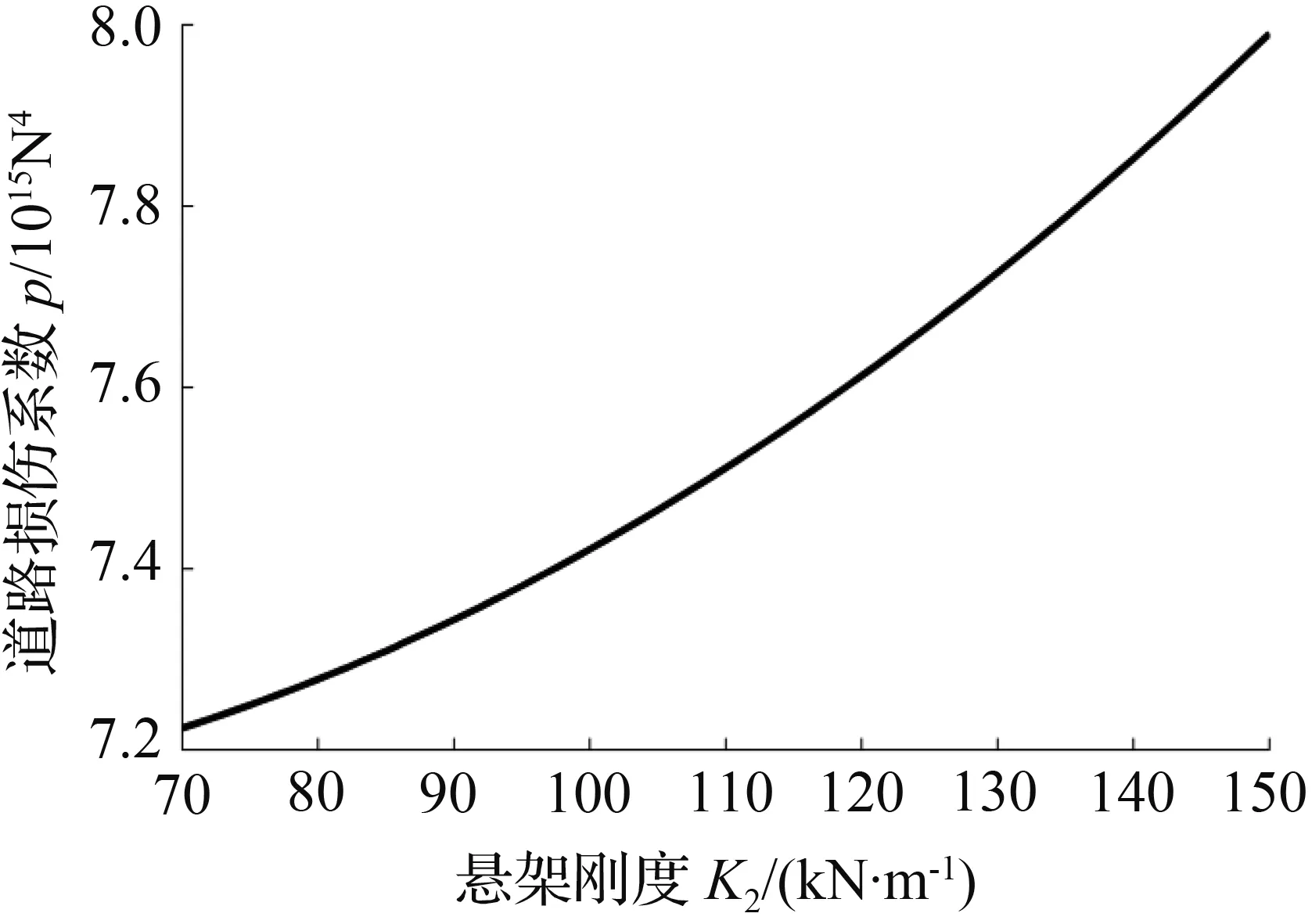
(c) 道路损伤系数p随悬架刚度K2的变化曲线

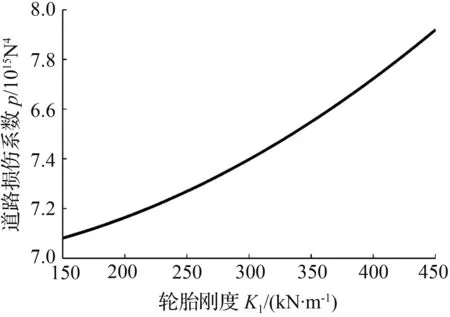
(d) 道路损伤系数p随轮胎刚度K1的变化曲线

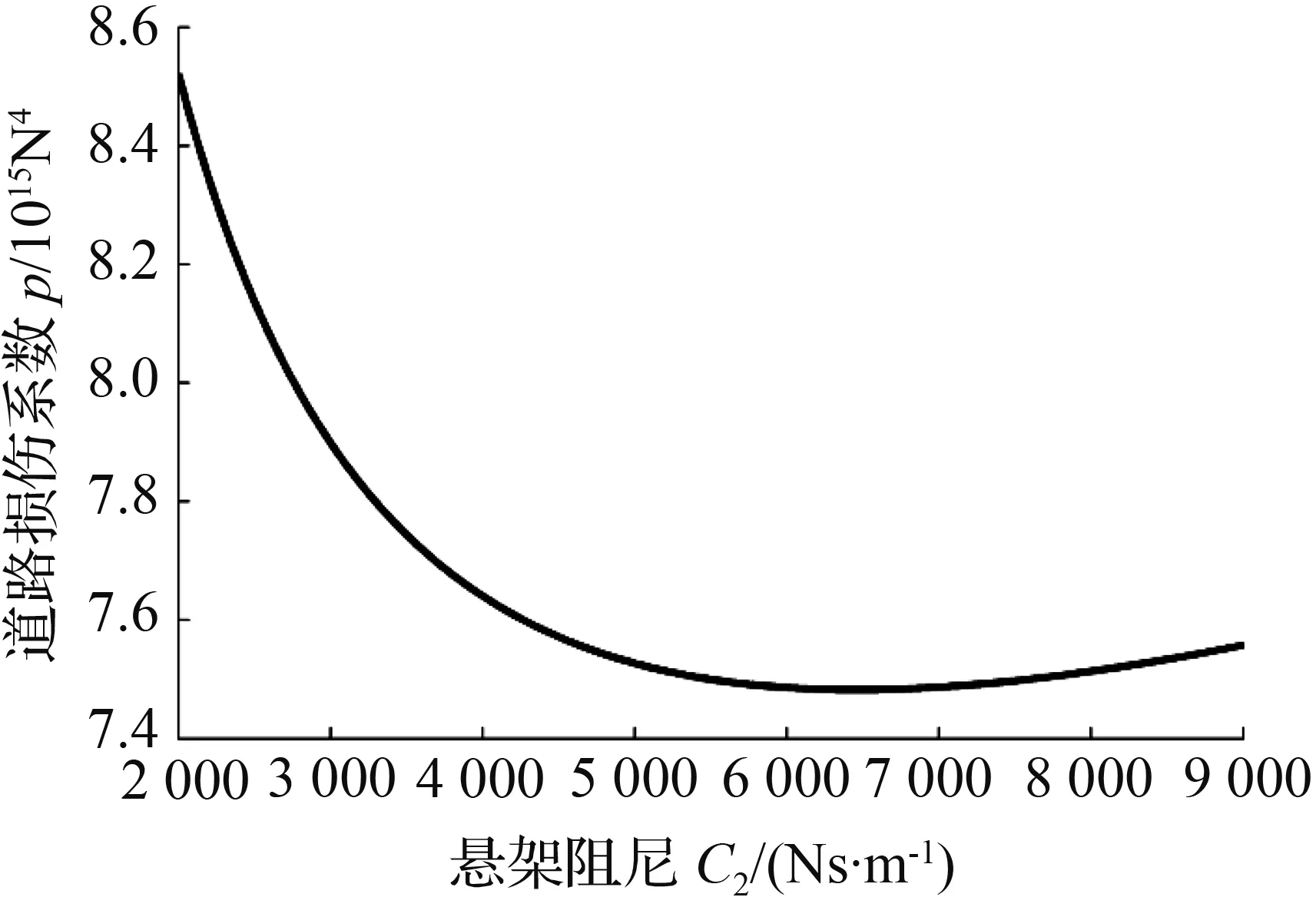
(e) 道路损伤系数p随悬架阻尼C2的变化曲线

3.2 车速及路况对道路损伤系数的影响

图3(a)和图3(b)分别为道路损伤系数p随车速v及路面功率谱密度Gq(n0)的变化曲线。图3(a)表明，道路损伤系数p与车速v近似成正比变化，故车速越高，车辆对路面的损伤越严重。由图3(b)可知，路面功率谱密度Gq(n0)不同，道路损伤系数p也不一样，且Gq(n0)越大则p越大。

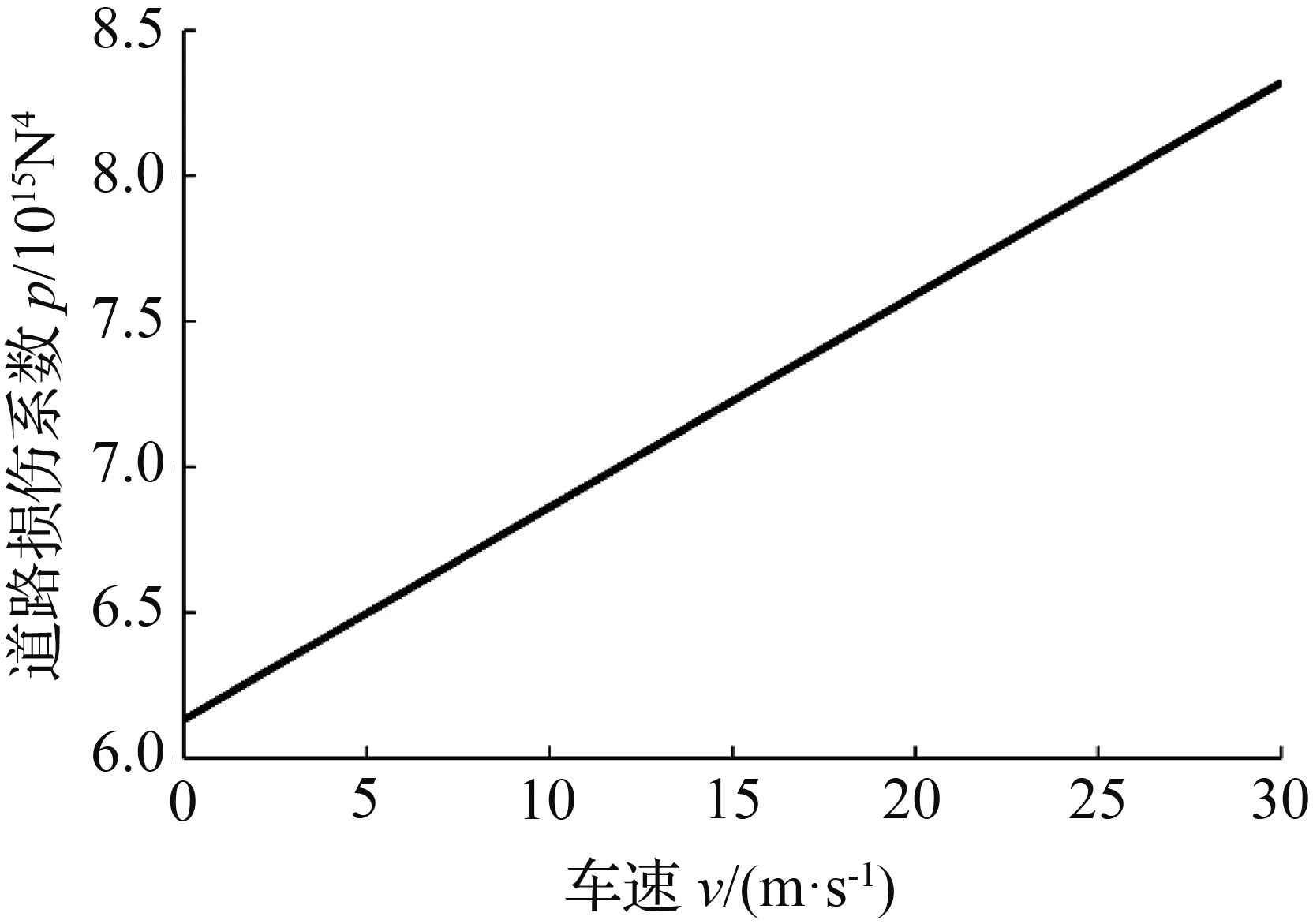
(a) 道路损伤系数p随车速v的变化曲线

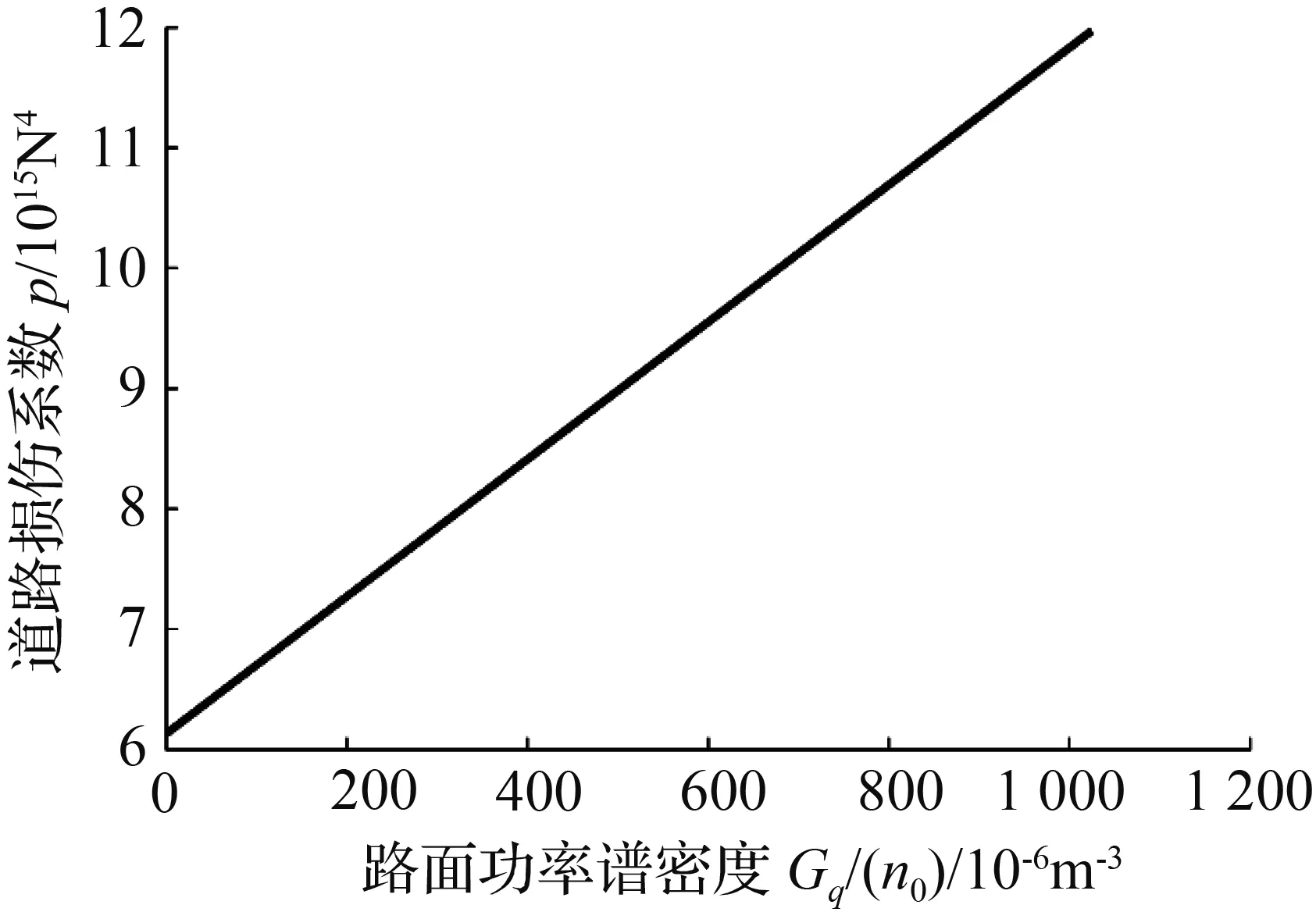
(b) 道路损伤系数p随路面功率谱密度Gq(n0)的变化曲线

图3 道路损伤系数p随车速v及谱密度Gq(n0)的变化曲线
Fig.3 Curves of road damage coefficient changing with running speed v and road power spectral densityGq(n0)

4 工程应用

为了提高车辆对道路的友好性，降低车轮对路面的破坏，以悬架系统阻尼C2为优化变量，以道路损伤系数p最小为优化目标，建立目标函数J如下:

min{J(ξ2)}=min{p}。

(14)

车辆悬架减振系统为小阻尼隔振系统，故满足如下约束条件:

(15)

可将上述问题，转化为有约束的数学优化问题，即为

(16)

将式(12)代入式(16)并进行求解，可得车辆悬架系统的最优阻尼为C2op，即：

(17)

式中，rm=m2/m1，rk=K1/K2。

例如，为了提高某微卡车辆的道路友好性，根据表1可得该车辆悬架系统的最优阻尼为C2op=6 460 Ns/m。该值与图2(e)中道路损伤系数p最小值对应的悬架阻尼C2的值吻合。结果表明，车辆悬架系统的最优阻尼C2op的解析计算式(17)是正确的，可为车辆悬架系统阻尼的匹配提供参考。

5 结论

①基于二自由度车—路系统动力学模型，根据道路损伤系数p的定义，推导得到了简洁的道路损伤系数解析计算式。

②道路损伤系数p与车辆行驶速度v、路面功率谱密度Gq(n0)及车辆参数有关。

③轮胎系统轻量化及降低车辆悬架刚度与轮胎垂向刚度，均有助于降低车辆对道路造成的损伤;悬架系统存在最优阻尼值使得道路损伤系数p最小化，故通过优化匹配悬架系统减振器也可提高车辆的道路友好性。

④基于道路损伤系数p解析式，推导得出了基于道路友好性的车辆悬架系统最优阻尼的解析计算式，为车辆悬架系统减振器的匹配和设计提供了理论依据。

本文给出的道路损伤系数p的解析计算式便于工程应用;此外，所揭示的规律可为降低车辆对道路的损伤提供有益参数。