基于主动噪声控制技术改善车内声品质

(江苏大学汽车与交通工程学院， 振动噪声实验室， 江苏镇江212013)

0 引言

主动噪声控制(active noise control)是依据声波干涉相消原理，利用次级声源发出一列幅值相等相位相反的声波，在目标区域和初级声源的声波叠加抵消，实现降噪[1]。随着该技术的广泛应用，车内噪声声压级得到明显降低，例如江苏大学的曾文杰[2]，利用ANC技术对车内发动机二阶频率的噪声进行主动降噪，实现了声压级15 dB的降噪量。但研究表明，声压级并不能完全反应人对噪声的主观感受，有时候声压级高的声音反而比声压级低的声音听起来更加悦耳，基于这种现象，研究学者提出了声品质的概念[3]。声品质反应人对声音的偏好性，一般用烦恼度来表示。影响声品质的客观参量主要有响度、粗糙度、尖锐度、A声压级、抖动度、语言清晰度等，客观参量的大小主要受频率和振幅的影响。因为ANC技术具有主动性，这就为声品质优化提供了一种行之有效的方法。

吉林大学刘宗巍等[4]利用ANC技术对驾驶员右耳处的噪声进行主动控制，评估了经过降噪后所取得的响度、尖锐度的变化情况；Oliveira等[5]评估了主动控制前后响度、粗糙度的改善情况；Lin等[6]采用主动控制系统进行降噪，对比了控制前后的语言清晰度。在基于声品质的主动噪声控制研究中，大多数研究人员只是采用主动噪声控制系统进行降噪，然后评估控制前后影响声品质客观参量的变化，并没有将声品质客观参量考虑进控制系统的设计中。

针对前人研究中存在的问题，本文利用遗传算法改进的神经网络(GA-BP)建立某款SUV稳态噪声的声品质预测模型,经过相关性计算，以对主观烦恼度影响最大的响度、粗糙度为控制目标，对响度从计算模型及Bark域上进行分析，对粗糙度进行小波分析，根据分析结果设计基于FELMS算法的ANC系统，并进行仿真验证，为改善车内声品质提供了可行、有效的方法。

1 声品质预测模型的建立

实车采集匀速工况下驾驶员耳旁的噪声信号，然后进行客观参量的计算和声品质的主观评价实验，利用GA-BP神经网络进行训练，建立声品质预测模型。

1.1 稳态噪声信号的采集

噪声采集仪器为HEAD-SQuadriga四通道便携式采集前端。根据奈奎斯特采样定理，采样频率设置为44 100 Hz，覆盖了人耳对声音的听觉范围(20～20 000 Hz)。在标准城市平坦道路上匀速行驶并进行测量，速度设置为怠速、10～80 kph(步长5 kph)，每个速度下采集3个样本，按照标准[7]，采集时车窗密闭、空调关闭、无外部车辆通过鸣笛等，否则删除该样本重新采集，本次共采集48个有效稳态噪声样本，采集环境及设备如图1所示。

(a) 采集环境 (b) 采集设备

1.2 声品质客观参量的计算以及主观评价试验

将采集的噪声信号导入Artemis软件的信号池中，为降低次声波对计算结果的影响，在滤波池中加入截止频率为20 Hz的高通滤波器，在分析池中加入响度、尖锐度、粗糙度、A声压级、声压级等5个声品质客观参量，选取各个参量的计算模型进行计算。主观评价试验可以通过组织评审人员进行听音试验，选择成对比较法打分规则并在相对安静的会议室进行，采用Sennheiser HD专业监听耳机回放噪声信号，剔除Kendall一致性系数低于0.75的评价数据，对声品质主观评价结果进行归一化处理，并以烦恼度等级表示，计算公式如式(1)：

(1)

因此烦恼度等级范围为0～9，烦恼度越高声品质越差，样本信号的客观参量计算结果及烦恼度等级如表1所示。

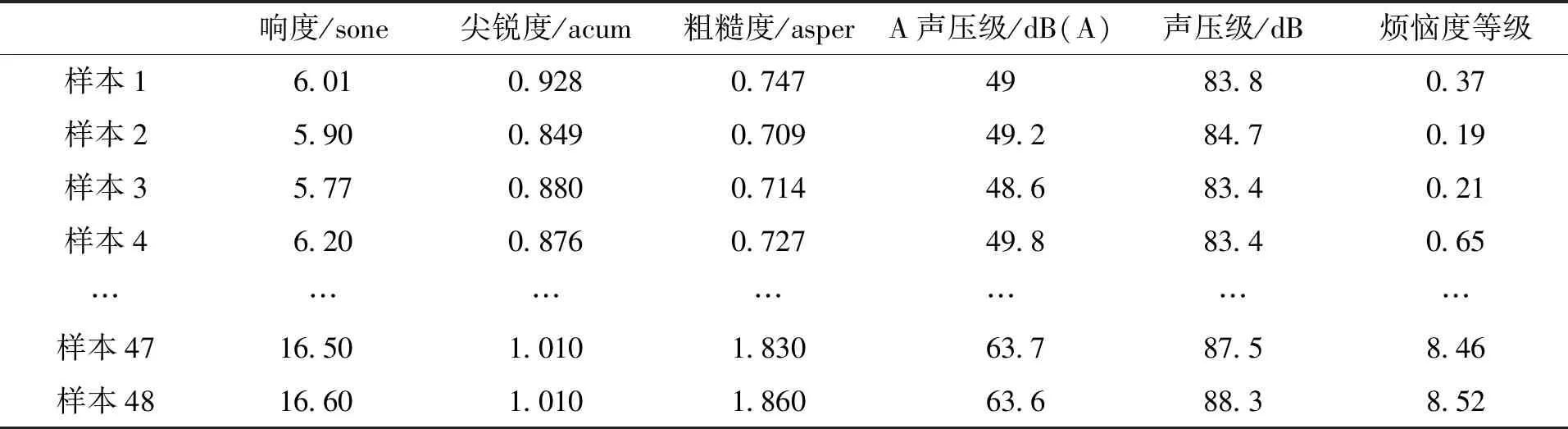
表1 客观参量计算结果及烦恼度等级Tab.1 Calculation results of objective parameters and the degree of annoyance

1.3 GA-BP声品质预测模型的建立

利用BP神经网络建立非线性声品质预测模型是目前广为使用的方法[8]，但BP神经网络对初始权值的选取非常敏感，容易陷入局部最小。引入遗传算法(GA)可以优化权值的选择，从而提高神经网络的全局搜索能力[9]。GA-BP神经网络中，以5个声品质客观参量为输入，以烦恼度等级为输出，综合考虑收敛步数及均方误差(MSE)选择隐含层个数为7，隐含层、输出层传递函数分别为Tansing、Purelin，学习算法为Traingd，最大遗传代数200，种群大小40，代沟0.85，交叉概率0.7，变异概率0.01。为保证神经网络模型训练精度以及验证的可靠性，一般选取总样本数的90 %作为训练样本，剩余10 %作为验证样本，所以选取44组样本信号作为训练样本，4组样本信号作为验证样本，GA优化BP神经网络处理流程及验证结果如图2、图3所示：

图2 GA优化BP神经网络处理流程图
Fig.2 Flow chart of GA optimized BP neural network

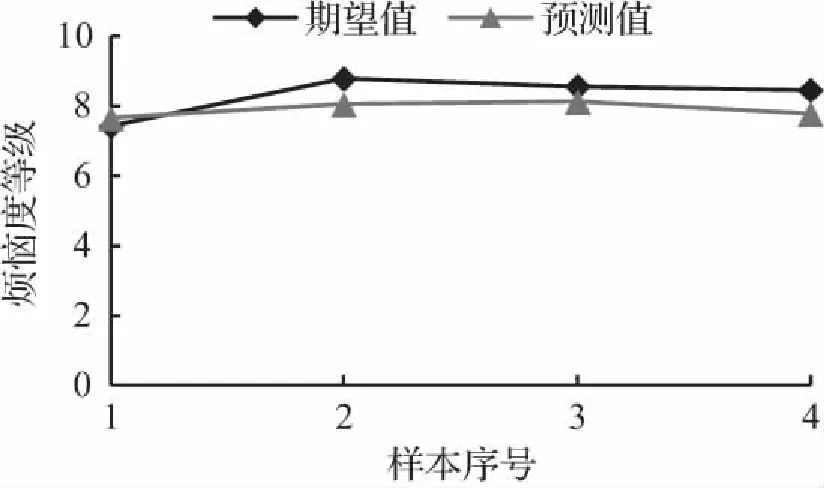
图3 GA-BP声品质预测模型输出值与期望值
Fig.3 Output and expectation of GA-BP processingacoustic quality prediction model

4组验证样本的误差分别为3.17 %、8.23 %、5.08 %、8.01 %，平均误差只有6.12 %，所建立的声品质预测模型具有较高的预测精度。

2 噪声信号分析

对客观参量和烦恼度进行线性回归分析，然后对与烦恼度相关性大的客观参量进行研究，找出最优的控制频段。

2.1 一元线性回归分析

在一元线性回归中,一般用皮尔逊相关系数R描述两个参量的关联程度，范围为(-1，1)，正负号代表正或负相关，绝对值越大，相关性越强。相关系数R的计算如式2所示。

(2)

分别以声压级、A声压级、响度、尖锐度、粗糙度为自变量，烦恼度为因变量进行一元线性回归，得出的相关系数如表2所示。

表2 客观参量与烦恼度的相关系数Tab.2 Coefficient of correlation between objective parameters and annoyance

RXY值在0.8以上表示X、Y显著相关，0.6～0.8表示相关，0.6以下就可以认为两个量之间弱相关或并无相关性。由表2可知，与烦恼度相关性从大到小依次是响度、粗糙度、A声压级、尖锐度、声压级，其中响度、粗糙度、A声压级显著相关。A声压级是选取40方等响曲线为计权曲线，对原声压级进行计权后的声压级，因此A声压级和响度是有一定的相似性，又因为被控的参量增多会导致控制算法性能下降，所以综合考虑客观参量与烦恼度的相关性以及主动噪声控制算法的收敛性，选取相关性最高的响度和显著相关的粗糙度作为主动噪声控制的控制变量。

2.2 响度及粗糙度分析

通过分析响度及粗糙度找出对其值影响最大的频段，为后续ANC系统的设计提供依据。抽取30号样本，对样本信号的响度、粗糙度进行分析。

响度的计算模型采取已形成国际标准的Zwicker模型，如式(3)所示,N′为特征响度。

(3)

(4)

由计算模型可以看出，噪声的响度N是每个临界频带内特征响度N′在Bark域的积分，在Artemis中，对样本信号进行Bark域下的响度分析及FFT分析，结果如图4、5所示。

由图4可知，最大特征响度max(N′)分布在第二临界频带，因此，响度的控制选择第二临界频带作为最优控制频段，从而实现针对性控制，第二临界频带所对应的频率范围为100～200 Hz，中心频率150 Hz。

粗糙度的计算模型采用常用的Fast1方法，公式如下所示：

(5)

其中fmod为调制频率，ΔLE(z)为声音的掩蔽深度。

图4 Bark 域下的响度分析
Fig.4 Loudness analysis in Bark domain

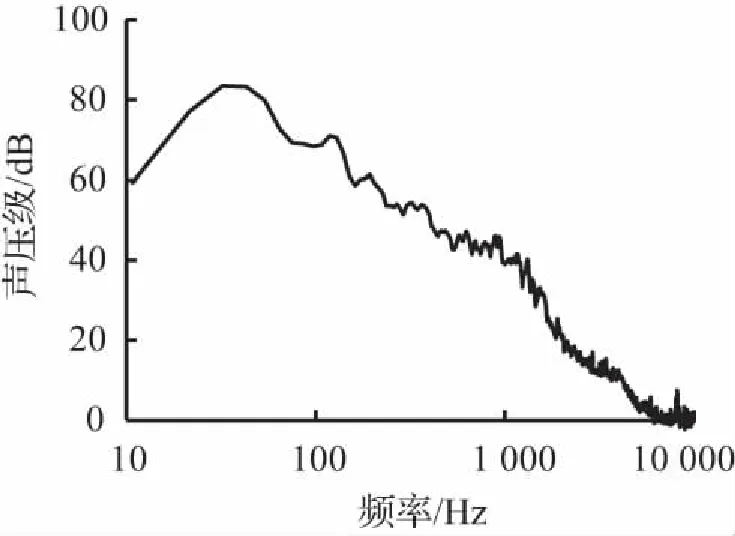
图5 FFT分析
Fig.5 FFT analysis

由公式(5)可以看出，粗糙度的大小主要和调制频率、调制深度有关，与响度计算模型不同的是，其值的计算并不是单一的量在Bark域下的积分，因此不能直接从计算模型上找出对粗糙度最关键的频段。根据图5的FFT分析结果，在6 000 Hz左右以后的声压级基本为0，所以样本信号的频率相对于采样最高频率22 050 Hz为低频，因此，利用小波分解[10]在低频段有较高的频率分辨率的特点，将原信号分解成若干个分量，然后将某分量置零进行小波重构，计算对比小波变换前后粗糙度的变化，从而确定粗糙度的最优控制频段。

小波分解分为连续小波分解和离散小波分解，相较于连续小波变换，离散小波变换可以减小小波变换的系数冗余度，小波变换基函数如下：

(6)

将小波变换基函数的a,τ限定在一些离散的点上取值，即可得到离散小波变换函数：

(7)

相应的离散小波变换可表示为：

(8)

在Matlab中，实现多尺度离散小波分解与重构的函数分别为wavedec、waverec。为尽可能的将样本信号的低频部分细分，选取N=12，即对原信号进行十二尺度分解,选取具有正交性的db4作为小波函数[11]。样本信号分解树及分解后的各分量如图6所示，由分解树可知，小波分解是在某一尺度下将信号按照频率分为低频、高频两部分，然后在下一尺度下再对低频部分进行分解，实现了对原信号低频部分的细分。

原信号S=a12+d12+d11+d10+d9+d8+d7+d6+d5+d4+d3+d2+d1，其中d1～d12为细节分量，即为某一尺度下的相对高频分量，a12为小波分解后剩余的近似分量，即为该尺度下的低频分量。细节分量dn对应的频率范围为(fs/2n+1,fs/2n)Hz，近似分量an对应的频率范围为(0,fs/2n+1)Hz，n=1，2，3…12为对应的尺度。近似分量a12和细节分量d12对应的频率分别为0～5 Hz、5～11 Hz，上文中虽已对原信号进行20 Hz的高通滤波，但受滤波性能的影响该频段仍有部分残余。

小波重构是小波分解的逆变换，形式上和分解树恰好相反，由最高尺度向最低尺度逐步重构得到重构信号。重构时的小波函数与分解时选取的一样，即db4小波函数。在重构过程中，分别将d1,d2,…,d12细节分量置零，重构后的信号为S-dn，表示已将dn分量置零，已知原信号S粗糙度为1.86 asper。

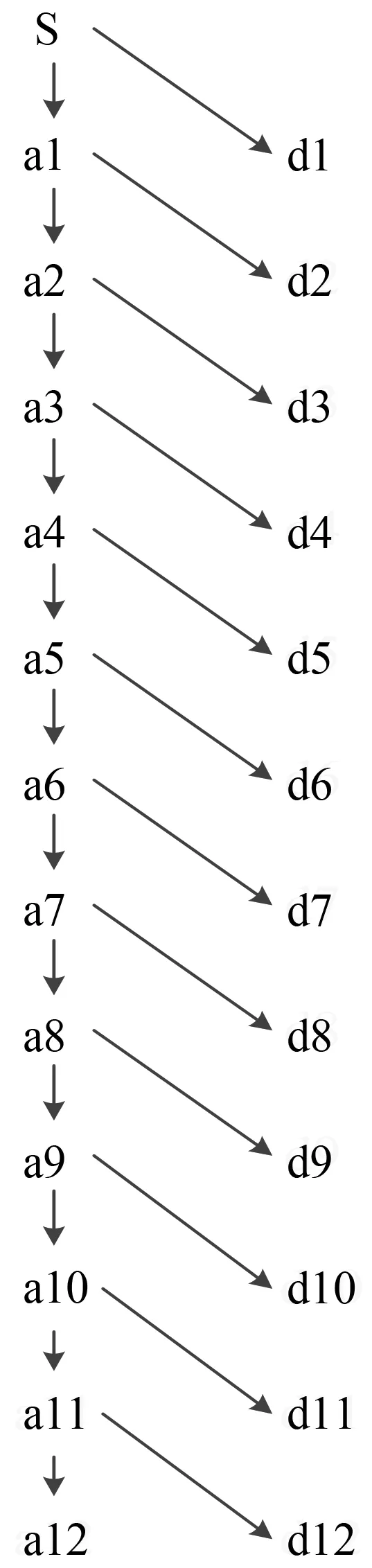
(a) 分解树

重构后信号的粗糙度计算结果如表3所示，可以看出，重构后的S-d10信号粗糙度下降幅度最大，为16.1 %，d10分量对应的频率段为22～43 Hz，对于该结果可以从粗糙度的定义进行解释。在原信号S中，d10分量会与其余频段的声音产生调制效应，由于人耳的听觉特性，当调制频率在20～300 Hz时，调制效应就表现为粗糙度，又由图6(b)可知，d10分量的幅值最大，因此，去除d10分量会降低掩蔽深度ΔLE(z)，进而使重构信号S-d10的粗糙度得到有效的降低，表明了利用小波变换对信号进行处理的正确性。

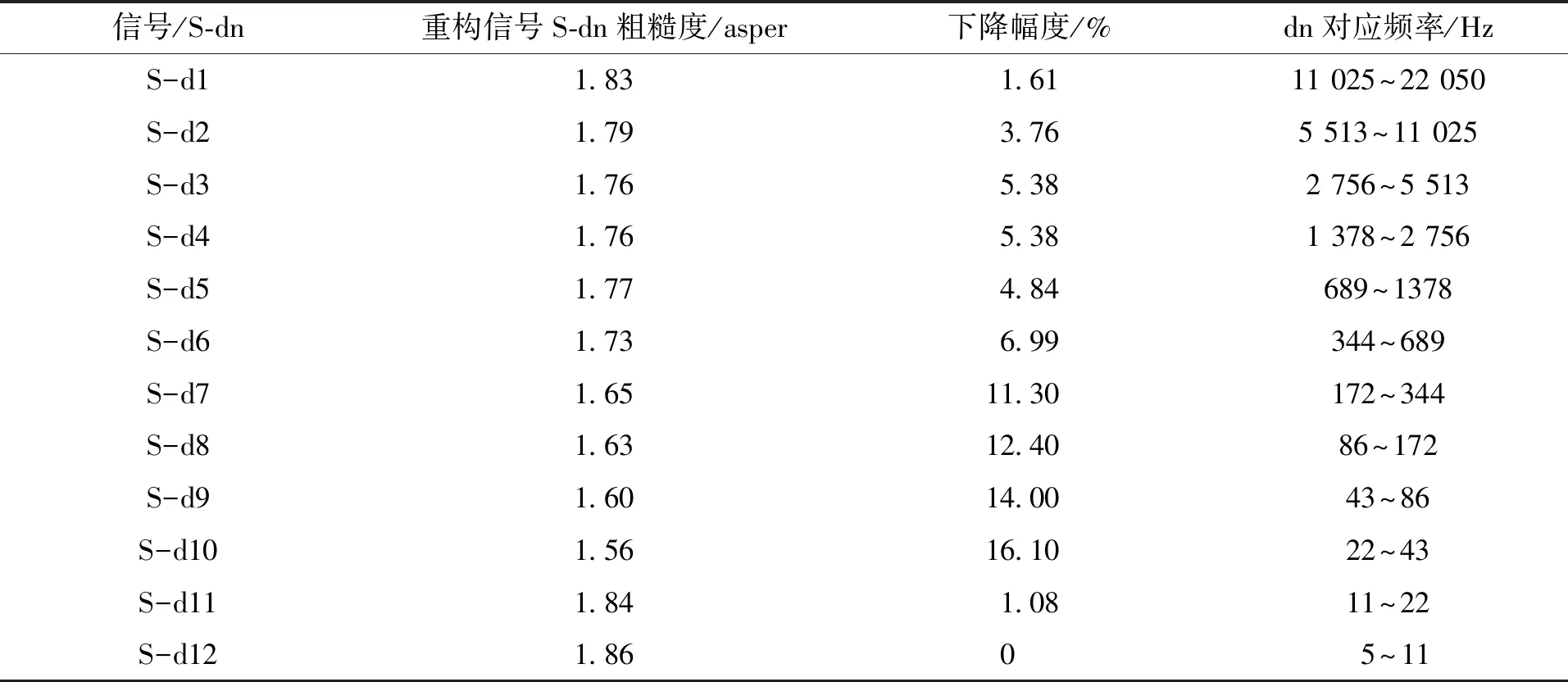
表3 小波变换后粗糙度的变化Tab.3 Changes in roughness after wavelet transform

针对粗糙度，经过对信号的小波分析，可以提出一个参数来表征小波分量对原信号粗糙度的影响。定义小波—粗糙度影响因子WAVE-Rn，单位为1，范围(0,1)，表征小波变换后dj细节分量对粗糙度的影响系数，其值越大，对粗糙度的影响越大，计算公式如下：

(9)

其中，S代表原信号；S-dn代表基于离散小波分解与重构,去除dn细节分量重构后的信号；RS表示原信号粗糙度；RS-dn表示去除dn细节分量重构后信号的粗糙度。

样本信号中，max(WAVE-Rn)=WAVE-R10=0.161，即d10细节分量对原信号粗糙度影响最大，对应的频率段为22～43 Hz。

3 主动噪声控制系统设计及仿真

对ANC控制算法进行分析，确定控制系统的框架。根据对响度、粗糙度的分析设计误差滤波器，然后将需要控制的信号作为输入，仿真得出控制后的噪声信号并计算其客观参量的值，将计算结果输入已建立的GA-BP声品质预测模型中，对比控制前后烦恼度的变化。

3.1 基于FELMS算法的主动噪声控制系统

LMS算法是ANC系统中重要的自适应滤波算法，该算法以设定目标值的均方根最小(least mean square)为目标进行迭代，滤波器根据计算结果实现权值系数的自适应调整。根据Windrows与Hoff提出的优化方法，下一时刻的滤波权值矢量W(n+1)可以表示为：

W(n+1)=W(n)-μ(n)，

(10)

其中，μ为收敛步长；(n)为第n次迭代的梯度，实际在LMS算法里，通常以误差信号的平方的梯度作为(n)的无偏估计，于是式(10)又可表示为：

W(n+1)=W(n)+μe(n)X(n)，

(11)

在LMS算法基础上，针对ANC系统中次级通道时延的问题，经过改进发展起来的FXLMS算法被广泛运用到以降低声压级为目的的主动噪声控制中。FELMS算法[12]在FXLMS的基础之上增加了误差滤波器对误差信号进行滤波，两种算法的控制系统框图如图7所示：

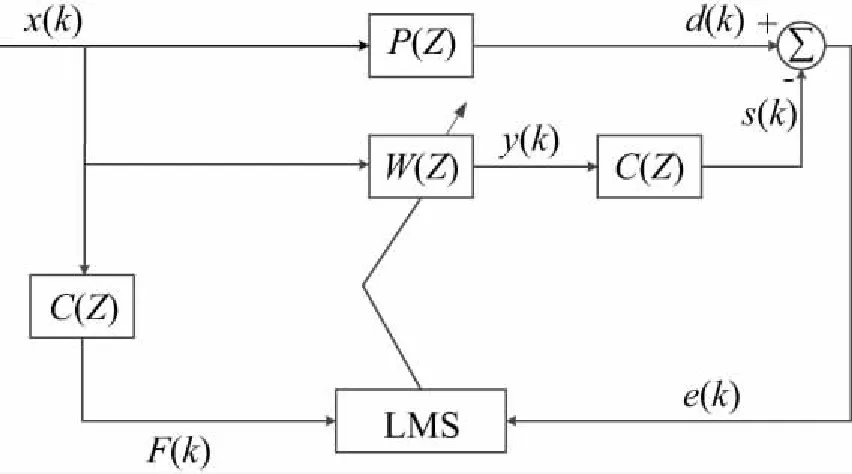
(a) FXLMS算法

(b) FELMS算法

图7 控制系统框架图
Fig.7 Framework diagram of control system

图7(b)中HW(Z)即为误差滤波器，F′(k)是参考信号x(k)经过次级通道估计函数C′(Z)和HW(Z)滤波后的信号，e′(k)是误差传感器拾取误差信号e(k) 经过HW(Z)滤波后的信号，LMS算法根据输入的F′(k)、e′(k)进行运算，滤波器W(Z)根据运算结果进行权值的调整，并发出控制信号y(k)，y(k)经过次级通道传递函数C(Z)到达目标区域和原噪声信号d(k)叠加。相较于FXLMS算法，由于FELMS算法增加了误差滤波器，不仅有效滤除车辆行驶中的干扰成分，而且只要合理设计误差滤波器的通带即可实现只针对噪声中的某频段进行选择性的抵消，从而达到改善声品质的目的。

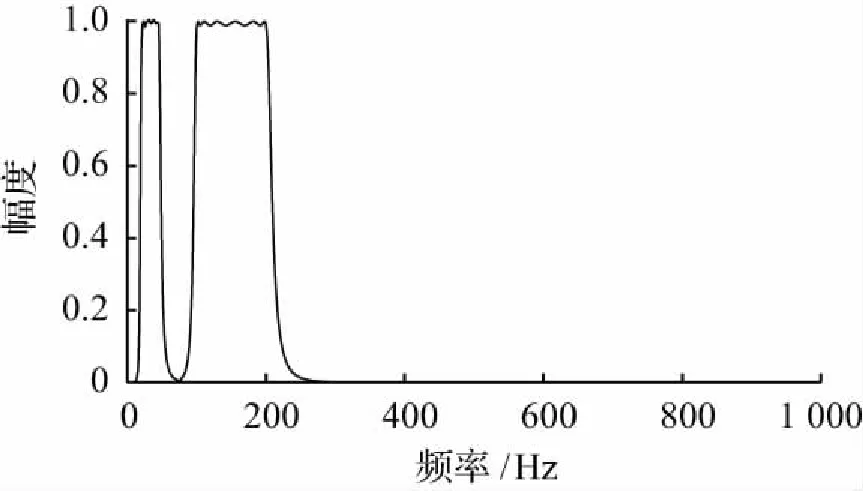
图8 误差滤波器频率响应曲线Fig.8 Frequency response curve of error filter

根据对样本信号的分析，响度的最优控制频带为最大特征响度所在的第二临界频带，粗糙度的最优控制频带为最大小波—粗糙度影响因子WAVE-Rn所对应的d10分量，因此设计HW(Z)为双带通滤波器，根据控制的参数的不同，两个通带可分别称为响度通带(通带频率100～200 Hz)和粗糙度通带(通带频率22～43 Hz)。

HW(Z)的设计基于频率响应误差小、频率截止速度快的切比雪夫Ⅰ型。设置fsl、fsu和fs1、fs2两个阻带截止频率以及fpl、fpu和fp1、fp2两个通带频率，衰减rp=0.1，仿真得出幅频特性，如图8所示，虽然在通带有纹波，但波动幅度小，不影响频率的幅值响应。

3.2 主动噪声控制仿真结果分析

为对比验证基于FELMS算法的主动噪声控制系统在声品质改善方面的优势，采用效率更高的C MEX S函数分别编写FELMS算法和FXLMS算法，并基于Matlab/Simulink工具箱，将ANC系统的各个模块进行封装，完成两种算法仿真模型的建立并进行仿真。

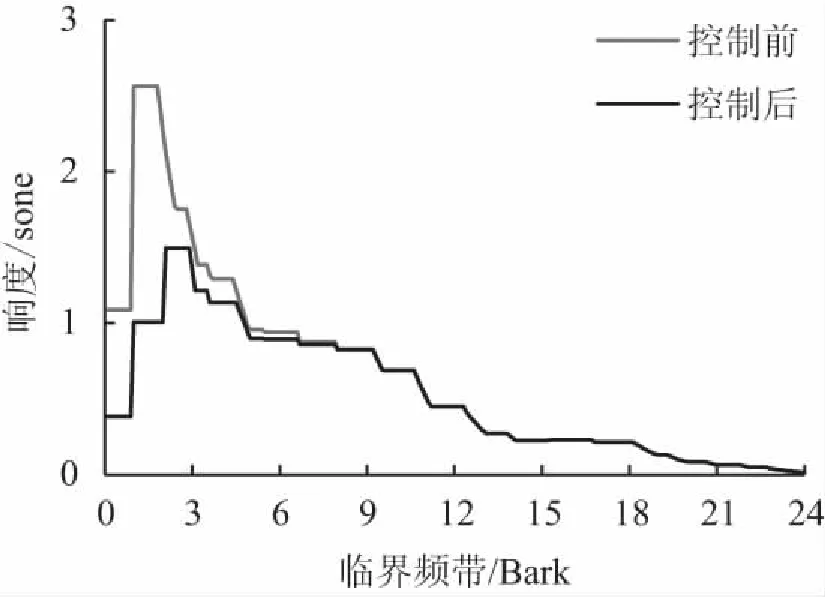
响度值的大小是特征响度在Bark域下的积分，控制前后响度在Bark域上的变化图9所示，从图9(a)曲线中可以看出，噪声信号的特征响度在0～24临界频带都有降低，但每个临界频带下的降低幅度小，总体响度由控制前的15.5 sone下降至11.4 sone，而图9(b)曲线中，虽然高临界频带的特征响度降低幅度更小，但因FELMS算法中误差滤波器存在响度通带(100～200 Hz)，可以实现对最大特征响度所在的频段进行针对性控制，所以该通带所对应的第二临界频带的特征响度有了大幅降低，总体响度由控制前的15.5 sone下降至10.3 sone，在响度控制效果上FELMS算法稍优。

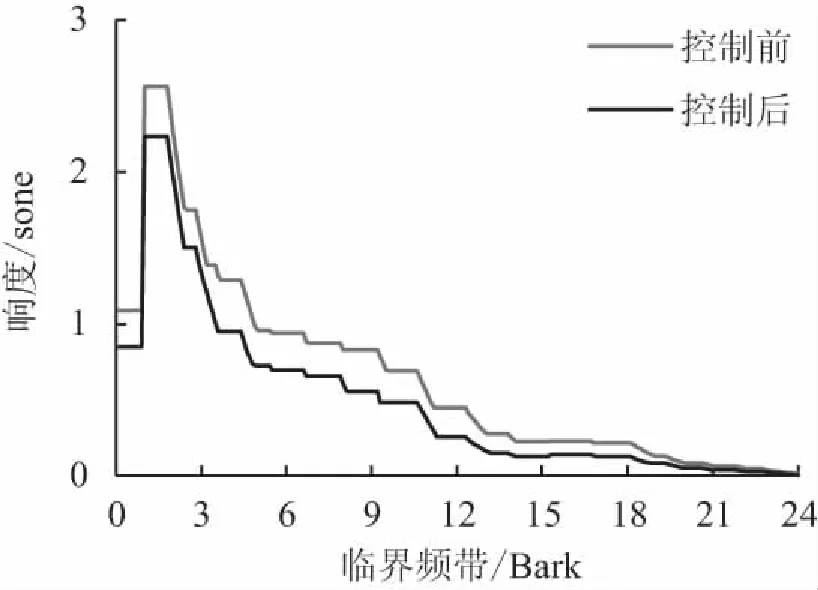
(a) FXLMS算法

(b) FELMS算法

图9 主动控制前后响度在Bark域上的变化
Fig.9 Changes of loudness in Bark domain before and after active control

相较于响度，粗糙度的大小不能从Bark域下观察出来，因此可以从时域上对比粗糙度在控制前后的变化，如图10所示：

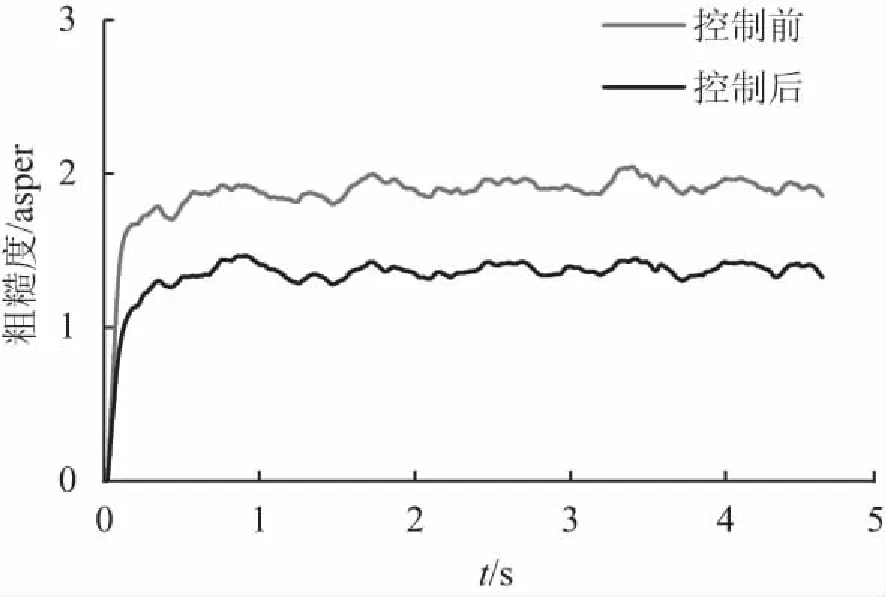
控制前的粗糙度为1.86 asper，基于FXLMS算法的控制系统对噪声的粗糙度基本没有影响，其值只降低了0.07 asper，而在基于FELMS算法的控制系统中，由于误差滤波器存在根据WAVE-Rn设计的粗糙度通带(22～43 Hz)，噪声的粗糙度从控制前的1.86 asper降低至控制后的1.43 asper，取得了23.1 %的降幅，控制效果明显。

(a) FXLMS算法

(b) FELMS算法

图10 主动控制前后粗糙度在时域上的变化
Fig.10 Changes of roughness in time domain before and after active control

计算控制后噪声的客观参量，如表4所示，可以看出，控制后的响度、粗糙度、声压级、A声压级都有降低，因尖锐度描述的是噪声信号中的高频成分，而FELMS算法中对相对低频部分(22～43 Hz、100～200 Hz)进行了针对性控制，导致了控制后噪声的高频部分占比增加，进而使尖锐度得到了0.11 acum的增加。

表4 控制前后的声品质客观参量值Tab.4 Objective parameters of sound quality before and after control

为对比主动控制前后声品质的变化情况，将控制前后的客观参量输入已建立的GA-BP声品质预测模型中得出客观预测值。为进一步验证控制效果，在保证听音环境及设备等条件与首次主观评价试验相同情况下，组织原评审人员对控制后的噪声再次进行主观评价试验。客观预测值与主观评价值的结果如图11所示，可以看出，主、客观烦恼度值基本一致，验证了所建立的GA-BP声品质预测模型的精度以及可靠性。

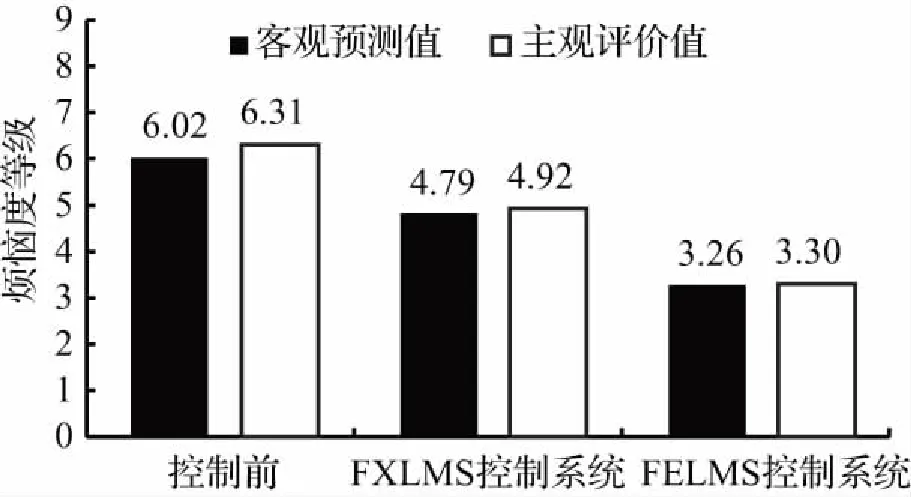
图11 控制前后烦恼度等级Fig.11 Level of distress before and after control

根据图11中的客观预测值，相较于控制前，基于FXLMS算法的ANC系统使车内声品质的烦恼度下降了1.23个等级，而基于FELMS算法的ANC系统使车内声品质的烦恼度下降了2.76个等级。结果表明基于响度、粗糙度设计的FELMS算法对车内声品质改善的效果是十分显著的，主观评价值也进一步验证了改善的有效性。

4 结论

本文针对某SUV车内声品质差的问题，经过对声品质客观参量的分析，利用主动噪声控制技术对声品质进行改善，取得了良好的改善效果，极大的提升了汽车舒适性，为该领域的研究提供了一定的参考。而且FELMS算法是对传统主动噪声控制系统中FXLMS算法的改进，只需在FXLMS算法上增加一个误差滤波器即可，因此十分便于在实际应用中的实现，具有较高的工程应用价值以及应用前景。研究的主要结论如下：

①以某款SUV稳态工况下车内噪声为研究对象，采集48组噪声样本，利用遗传算法优化的神经网络建立了GA-BP声品质预测模型并进行验证，结果表明，预测模型平均误差仅为6.12 %，具有较高的精度。

②将声品质客观参量分别和烦恼度进行一元线性回归分析，结果表明，响度、粗糙度和烦恼度相关性最大。对响度从计算模型上分析，选取最大特征响度对应的临界频带为响度最优控制频段。对粗糙度进行小波分析，基于小波变换前后的粗糙度提出参数小波—粗糙度影响因子WAVE-Rn，选取最大WAVE-Rn所对应的频段为粗糙度最优控制频段。

③根据对响度、粗糙度的分析结果设计误差滤波器，并建立基于FELMS算法的ANC系统进行仿真。结果表明，经过主动噪声控制，响度、粗糙度分别降低了33.5 %、23.1 %，烦恼度下降了2.76个等级，控制效果明显优于传统的FXLMS算法，证明了所设计的FELMS算法对车内声品质的改善是可行的，且效果显著。