基于多方向Gabor特征图稀疏表示的鲁棒人脸识别方法
徐望明, 张培, 伍世虔
(1.武汉科技大学 信息科学与工程学院,湖北,武汉 430081; 2.武汉科技大学 教育部冶金自动化与检测技术工程研究中心,湖北,武汉 430081; 3.武汉科技大学 机械自动化学院,湖北,武汉 430081; 4.武汉科技大学 机器人与智能系统研究院,湖北,武汉 430081)
经过近几十年的发展,人脸识别技术已取得巨大进步,出现了一些有代表性的识别算法[1-2],但是这些人脸识别算法在实际应用中受到诸多条件的制约,比如光照、表情以及姿态变化等. 提升算法在这些制约条件下的鲁棒性既是人脸识别技术的研究难点,也是研究热点. 为了解决人脸识别技术中存在的这些问题,Wright等[3]提出了一种基于稀疏表示分类的人脸识别方法(sparse representation based classification,SRC).相比于文献[1-2]等经典的人脸识别算法,SRC算法不仅提高了对光照、表情、姿态等可变因素的不敏感性,而且对遮挡、噪声也具备一定的鲁棒性.
很多研究学者在SRC人脸识别方法的基础上做了大量改进工作[4-5]. 这类方法基于人脸图像的全局特征,对光照、姿态、表情等因素的适应性仍存在局限性. 考虑到LBP、Gabor等局部特征在人脸识别任务中能够很好地获取人脸图像局部的纹理信息,且对光照变化不敏感,Yang等[6]提出基于Gabor特征稀疏表示(Gabor-feature based SRC,GSRC)的人脸识别方法,提取不同尺度和方向的Gabor特征,提取的局部Gabor特征比全局特征包含更多人脸纹理信息,从而具有更好的识别效果,但是提取的多方向多尺度的Gabor特征存在信息冗余. 刘帅师等[7]提出一种基于Gabor特征融合的人脸表情识别方法,对多方向多尺度的Gabor特征进行同一尺度不同方向的特征融合,这种融合策略使得人脸特征得以降维,从而提高运算效率,同时融合后的特征图也具备较好的纹理信息,能够对表情变化有很好的鲁棒性.
为了进一步解决基于稀疏表示的人脸识别算法对光照、表情、姿态等可变因素敏感的问题,本文提出了一种基于多方向Gabor特征图稀疏表示的人脸识别方法(multi-directional Gabor feature maps based SRC,MGFM-SRC),对人脸图像的多方向Gabor特征图提取自适应加权的Gist特征,并利用稀疏表示分类器实现人脸识别.
在Yale、ORL和Extended Yale B人脸数据库上的实验结果表明,本文提出的人脸识别方法相比于其它基于SRC的人脸识别方法提高了识别准确率.
1 多方向Gabor特征图的自适应加权Gist特征提取
本文提出的基于稀疏表示的人脸识别方法. 先对人脸图像进行多方向多尺度Gabor变换,得到了不同方向和尺度的Gabor实部特征和虚部特征,然后分别将同一方向不同尺度的Gabor实部特征和虚部特征采用二进制融合规则得到多方向Gabor幅值特征图,又对每个方向的幅值特征图提取Gist特征并赋予自适应权重,接着将所有方向特征图的自适应加权Gist特征串联构成人脸特征向量. Gabor变换能够很好地提取人脸图像局部纹理信息,而Gist特征又能够很好地描述图像的全局形状信息,结合这两种特征能有效提高人脸识别的鲁棒性. 如图1所示,特征提取主要步骤分为:多方向多尺度Gabor变换、Gabor特征融合、多方向融合特征图的自适应加权Gist特征计算.

图1 人脸图像加权Gist特征提取Fig.1 Weighted Gist feature extraction for face image
1.1 多方向多尺度Gabor变换
二维Gabor核函数[8]定义为
(1)
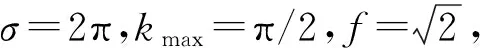
Mu,v(z)=I(z)*gu,v(z).
(2)
式中:I(z)为灰度人脸图像;*为卷积操作符;gu,v(z)为Gabor滤波器;Mu,v(z)为滤波得到的不同方向和尺度的Gabor特征图. 如图1中的Gabor实部和虚部特征图所示,其中各行特征图对应不同的方向,各列特征图对应不同.
1.2 Gabor特征融合
从Gabor实部和虚部特征图中可以看出:一方面,对于多尺度和多方向的Gabor特征所包含的人脸特征信息存在一定程度冗余,使用全部特征图的信息必将提高后续人脸识别算法的计算复杂度;另一方面,对于同一个方向的特征图,随着尺度变大,Gabor特征图中所包含的局部信息逐渐变少,人脸图像的全局轮廓信息逐渐变得明显. 为了减少后续人脸识别算法的计算复杂度,同时保留更多的局部纹理信息以提升人脸识别的性能,本文提出一种对同一方向不同尺度Gabor特征进行融合的方法.
首先,根据Gabor实部特征Re(Mu,v(z))和虚部特征Im(Mu,v(z))的符号进行二进制编码:
(3)

(4)
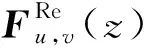
然后,分别对同一方向不同尺度的二值特征图进行加权融合十进制编码形式:
(5)
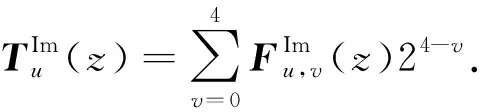
(6)
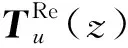
最后,用融合后实、虚部特征求幅值特征图:
(7)
如图1中融合后的幅值特征图所示,减少Gabor特征冗余信息的同时,也包含了人脸比较明显的局部纹理信息.
1.3 自适应加权Gist特征计算
Oliva等[10]提出的Gist特征能够模拟人的视觉捕获图像中的全局信息,常用于场景图像分类任务. Gist特征提取方法的主要原理是:利用Gabor滤波器组对输入图像进行卷积处理,将滤波结果图像划分为均等不重叠的l×l个图像子块,并对每个图像子块取灰度平均值,把所有图像子块的灰度平均值串联起来即形成表示图像的特征向量.
本文以上述融合后的幅值特征图作为输入图像,进一步提取其Gist特征形成人脸图像的全局表示,用于人脸识别任务. 同时考虑到每个融合后的幅值特征图所包含的纹理信息不同,本文采用香农信息熵来度量其纹理信息丰富程度,并依据信息熵为不同方向特征图的Gist特征进行自适应加权.
本文方法在计算Gist特征时取l=4,并采用8个方向、4个尺度共32个Gabor滤波器参与卷积运算. 自适应加权Gist特征计算的具体步骤如下.
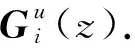
(8)
式中:z为像素的坐标;gi为第i个Gabor滤波器;u=0,1,…,7;i=1,2,…,32.
(9)
式中:Cat表示特征串联操作符,j=1,2,…,16.
④ 对于每个融合后的幅值特征图Mu(z),其信息熵为
(10)
式中:L表示融合后幅值特征图Mu(z)中像素灰度最大值;pu,m表示第u个特征图中灰度值为m的像素出现的概率. 根据信息熵理论得知,信息熵越大,图像所包含的信息越多,则在本文方法中赋予对应图像Gist特征更大的权重,权值计算如下:
(11)
⑤ 将每个融合后的幅值特征图Mu(z)的Gist特征Gu进行归一化,记为Su(u=0,1,…,7),将所有加权的Gist特征串联形成最终人脸图像的特征向量b,其中
b=[w0S0w1S1…w7S7]T,
w0+w1+…+w7=1.
2 利用稀疏表示分类实现人脸识别
2.1 稀疏表示分类识别人脸方法的基本原理
文献[3]进行人脸识别的一个前提条件是:同一个类别的训练样本属于同一子空间,每一个测试样本属于对应类别的子空间. 定义第i类的训练样本组成的特征矩阵为
Ai=[vi,1vi,2…vi,ni]∈Rm×ni.
式中:vi,j为第i类的第j个样本的特征向量;m为特征向量的维度;ni表示第i类样本的个数. 对于属于第i类的测试样本y∈Rm×1,可以由Ai线性表示为y=Aixi,其中xi=[xi,1xi,2…xi,ni]T.
有k个类别足够多的训练样本,所有训练样本的特征矩阵为
A=[A1A2…Ak]=
[v1,1…vi,ni…vk,nk]∈Rm×n,
式中n=n1+n2+…+nk,n表示所有训练样本的个数,理想情况下y可以由A线性表示为y=Ax,其中
x=[0…xi,1…xi,ni…0]T.
x可看作测试样本在训练样本特征矩阵作为字典时的稀疏表示系数,在求解该系数时,希望对应第i类训练样本的系数较大,而对应其它类训练样本的系数较小或为0.
SRC人脸识别算法的主要步骤如下.
① 对输入的A和y利用L2范数归一化.
② 按L1范数最小化[9]求稀疏表示系数:
(12)
③ 计算重构误差:
(13)

④ 依重构误差最小化原则判定识别结果为
identity(y)=argminri(y).
(14)
2.2 本文提出的稀疏表示人脸识别方法
本文利用所提出的多方向Gabor特征图的自适应加权Gist特征提取方法(MGFM)与上述稀疏表示分类方法(SRC)相结合实现人脸识别. 本文算法MGFM-SRC可描述如下.
给定k个类别的足够多的训练样本,将所有的训练样本按照本文提出的特征提取方法提取每个样本的人脸特征向量,然后所有的人脸特征矩阵为B=[B1B2…Bk]=[b1,1…bi,ni…bk,nk]∈Rc×n.
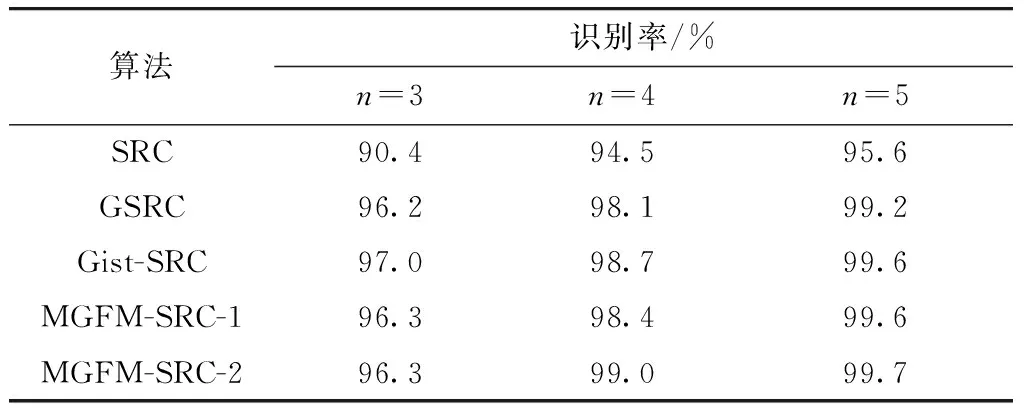
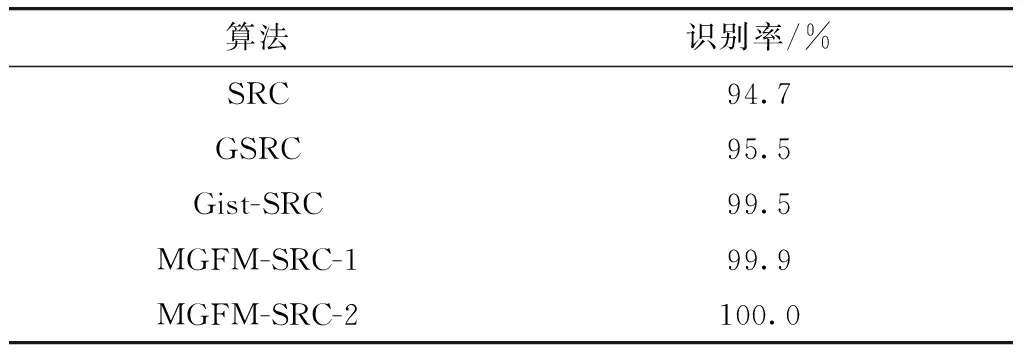
式中:bi,j表示第i类的第j个训练样本人脸特征向量;c为特征向量的维度;n(n=n1+n2+…+nk)为所有训练样本个数. 给定属于i类测试样本也按照本文特征提取算法提取特征向量φ∈Rc×1. 考虑到本文提取人脸特征向量的维度比较高,为了提高计算效率,利用主成分分析(principal component analysis,PCA)产生一个变换矩阵ψ∈RK×c,其中K(K Q=Φx=Φ1x1+Φ2x2+…+Φkxk. (15) 将式(15)中的字典矩阵Φ和特征向量Q分别代替式(12)~(14)中的A和y,依据重构误差最小化原则得到人脸识别结果. 本文算法MGFM-SRC的具体步骤如下. ① 对人脸图像I(z)利用式(1)中Gabor滤波器组提取不同方向和尺度人脸图像的Gabor特征Μu,v(z). ② 将得到的不同方向和尺度的Gabor实部特征和虚部特征利用式(3)~(7)按同一方向不同尺度进行特征融合,最后得到8个方向的融合的特征图Mu(z)(u=0,1,…,7). ③ 对每个方向融合的特征图Mu(z)利用式(8)和式(9)得到图像的Gist特征Gu(u=0,1,…,7),对每个融合的特征图像的Gist特征进行归一化,记为Su(u=0,1,…,7),再利用式(10)和式(11)求取不同方向特征图的权重wu(u=0,1,…,7),最后将所有加权的Gist特征串联形成表示一幅人脸图像的特征向量b,其中 b=[w0S0w1S1…w7S7]T, w0+w1+…+w7=1. 为便于在实验中比较自适应加权所起的作用,这里记不使用加权策略的方法为MGFM-SRC-1,使用了加权策略的方法为MGFM-SRC-2. ④ 将所有的训练样本的特征集组成训练样本特征矩阵B=[B1B2…Bk]∈Rc×n,利用PCA降维得到变换矩阵ψ,对训练样本特征矩阵降维构成用于稀疏表示的字典矩阵:Φ=ψB,并对字典矩阵Φ进行L2范数归一化. ⑥ 利用式(13)求解测试样本的人脸特征向量对应于各个类别的稀疏重构误差,并根据式(14)所示的重构误差最小化原则判定人脸识别结果. SRC算法、GSRC算法、Gist-SRC算法、MGFM-SRC-1算法以及MGFM-SRC-2算法分别在Yale[2]、ORL、Extended Yale B等典型人脸数据库上进行了实验比较. 设置SRC算法中λ=0.05,其他算法中λ=0.001. 在Yale人脸库上,比较了特征维度对各个算法的影响;在ORL人脸库上,比较了训练样本个数对各个算法的影响;在Extended Yale B人脸库上,比较了光照变化对各个算法的影响. Yale数据库包含15个人每个人11幅在不同光照、表情和姿态下的正面人脸图像,共165幅. 本文随机选取每类5幅人脸图像作为训练集字典,剩余的作为测试样本,将人脸图像裁剪和归一化为32×32,10次实验取平均值,比较不同维度m下各个算法的识别率,如表1所示. 表1 在Yale数据库不同算法的识别率 Tab.1 Recognition results of different methods on the Yale database 算法识别率/%m=10m=30m=50m=60m=70SRC75.283.183.284.785.3GSRC76.086.188.289.788.4Gist-SRC88.495.197.998.699.0MGFM-SRC-187.297.098.699.498.6MGFM-SRC-287.897.399.299.899.8 从表1可见,当数据维度为10时,Gist-SRC算法识别率最高,本文算法与之也很接近;但随着数据维度升高,各个算法识别率也逐步上升. 相对于SRC算法,其他算法识别率均有更大幅度提升,说明基于局部特征的稀疏表示算法对光照、姿态以及表情有更好鲁棒性. MGFM-SRC-2算法比Gist-SRC算法和MGFM-SRC-1算法的识别率高,说明MGFM-SRC-2算法进一步克服了光照、表情以及姿态等因素变化对人脸识别带来的影响. ORL人脸数据库包含40个人、每人10幅不同光照、表情以及姿态下的人脸图像,总共400幅人脸样本. 将人脸图像裁剪和归一化为32×32,根据选取的每类训练样本个数不同分为3组实验,每组10次实验取平均值,验证改变每类训练样本个数n对各个算法人脸识别率的影响. 结果如表2所示. 表2 在ORL数据库不同算法的识别率 Tab.2 Recognition results of different methods on the ORL database 算法识别率/%n=3n=4n=5SRC90.494.595.6GSRC96.298.199.2Gist-SRC97.098.799.6MGFM-SRC-196.398.499.6MGFM-SRC-296.399.099.7 可见,当训练样本数为3时,Gist-SRC算法效果最好,本文算法MGFM-SRC-1和MGFM-SRC-2与之接近;随着训练样本数增加,MGFM-SRC-2算法的优势体现出来,相对于其他算法识别率均有所提升,且处于最高位置. 这说明基于Gabor特征构造的稀疏表示字典,有助于提高识别率,同时MGFM-SRC-2算法对不同方向融合的Gabor特征赋予了自适应的权重,凸显出不同方向特征图的重要性,因而取得了更好的识别效果. Extended Yale B人脸数据库中包含38个人每个人64幅在不同光照条件下的正面人脸图像,共有2 432幅图像. 将人脸图像裁剪和归一化为54×48,本文随机选取每类32幅人脸图像作为训练集字典,剩余的作为测试样本,5次实验取平均值. 表3给出了各个算法在同样的条件下进行实验比较的结果. 表3 在Extended Yale B数据库不同算法的识别率 Tab.3 Recognition results of different methods on the Extended Yale B database 算法识别率/%SRC94.7GSRC95.5Gist-SRC99.5MGFM-SRC-199.9MGFM-SRC-2100.0 可见本文算法MGFM-SRC-1和MGFM-SRC-2的识别率高于SRC算法、GSRC算法以及Gist-SRC算法. 使用了自适应加权策略的MGFM-SRC-2算法平均识别率达到100.0%,优于未使用自适应加权策略的MGFM-SRC-1算法的识别率,这说明不同方向的融合特征图的表征能力不一样,赋予重要方向特征图更大的权重,有利于提高识别率. 提出了一种基于多方向Gabor特征图稀疏表示的人脸识别方法,能有效的克服光照、姿态和表情等因素变化对人脸识别性能的影响,提升人脸识别准确率. 本文方法的特点在于:①Gabor变换能够很好的提取人脸图像局部纹理信息,而Gist特征又能够很好的描述图像的全局形状信息,本文方法结合了这两种特征,能有效的提高人脸识别的鲁棒性;②多尺度和多方向的Gabor特征图存在信息冗余,而且对于同一个方向的特征图,随着尺度变大所含局部信息逐渐变少、全局轮廓信息逐渐明显,本文方法实现了对同一方向不同尺度的Gabor特征图进行融合,减少了后续人脸识别算法的计算复杂度,同时保留了更多的局部纹理信息以提升人脸识别的性能;③为了突显每个融合后的特征图所包含的纹理信息的重要性,本文方法采用了香农信息熵来度量其纹理信息丰富程度,并依据信息熵为不同方向特征图的Gist特征进行自适应加权,以加权Gist特征作为人脸图像的全局表示,在此基础上使用稀疏表示分类方法实现人脸识别. 实验结果表明,与以上分析的算法相比,本文方法对光照、姿态、表情等可变因素的鲁棒性更强,取得了更高的识别准确率.
3 实验结果与分析
3.1 在Yale人脸数据库上的实验

3.2 在ORL人脸数据库上的实验
3.3 在Extended Yale B人脸数据库上的实验
4 结 论

