基于气固两相DEM模型的相对旋转式喂料头的研究
孙晓霞, 孟文俊, 牛雪梅, 袁媛
(1.太原科技大学 机械工程学院,山西,太原 030024; 2.山西能源学院,山西,太原 030024)
随着垂直螺旋输送机的广泛应用,作为其重要组成部分的取料装置也有了各种形式,其中最重要的一种形式就是相对旋转式喂料头(简称喂料头),其喂料量和喂料效率关系到输送机的输送效率[1-2]. 在国际上,垂直螺旋输送机及其喂料头的技术相对先进,提出了如多片导料挡板式反向旋转喂料头、双口螺线式喂料头、螺旋挡板式喂料头、倾斜翼板式喂料头等多种结构的喂料头[3].对喂料头的研制是通过试验,测得不同尺寸的喂料头模型在不同的喂料头转速的情况下的充填率、功率及生产率,由试验曲线描述取料段性能指标随喂料头结构参数的变化规律,确定较佳的设计变量. 相对于国外先进的技术优势,喂料头在我国目前尚未有统一的标准,每个厂家都有各自的加工标准和输送量确定的标准.
喂料头的喂料效率和喂料量直接影响到垂直螺旋输送机的输送效率,而对喂料头的喂料量产生影响的主要因素就是喂料头的喂料曲面. 因此,喂料曲面的投影、展开平面以及特征曲线的形状及方程也是各有特点. 颗粒进入喂料头后,由于料壁内螺旋的高速旋转,会产生气流影响颗粒的运动,所以对于喂料头中的颗粒,不仅要考虑颗粒与颗粒、喂料头之间的相互作用,还要考虑颗粒与气体之间的相互作用. 颗粒在喂料头中的运动比较复杂,受力也比较复杂,难以在理论上深入探讨颗粒在喂料头中的运动过程[4].
近年来,随着计算机技术的快速发展,数值模拟已逐渐成为与试验手段相辅相成的研究工具. 宋斌等[5-6]采用DEM模型及EDEM软件仿真对喂料头进行了研究,分析了垂直螺旋输送机内颗粒在不同条件下的运动情况,得出影响颗粒运动的因素. 但是喂料头中需要考虑气体对颗粒的作用,所以需考虑一种数值模型,不仅需要考虑颗粒与颗粒、喂料头之间的相互作用,还要考虑颗粒与气体之间的相互作用[7]. 文中采用E/L法对垂直螺旋输送机进行模拟,由于颗粒密度较高,颗粒之间的碰撞不能忽略,而离散单元法(DEM)是颗粒碰撞模型中最应用广泛的一种. 对于模拟喂料头这种复杂的颗粒流系统,建立气固两相DEM模型,采用离散单元法和计算流体力学(CFD)相结合的方式,可以跟踪每个颗粒的运动,获得大量的微观信息. 在DEM模型及其仿真的方法基础上,结合理论分析与气固两相DEM模型,及DEM+CFD耦合仿真分析颗粒的喂料过程,考察颗粒在不同曲面喂料头中的运动状态及输送量情况.
1 气固两相DEM模型及其仿真方法
在喂料头中,因为颗粒所受外力及摩擦力的复杂性和不确定性,难以用传统的牛顿第二定律的方法来确定颗粒的速度,而且,颗粒还受到空气的影响,因此,下面采用气固两相DEM模型及其仿真分析方法来观察颗粒的输送量情况.
1.1 气固两相DEM模型
1.1.1 颗粒固相控制方程
在气固两相DEM模型中,颗粒的运动通过求解牛顿第二定律获得,
ma=Fg+Fp-p+Fp-g+Fge,
(1)
式中:a为固相颗粒对于喂料叶片的加速度;Fg为重力;方向垂直向下;Fp-p为颗粒与颗粒、喂料叶片之间的作用力,方向不确定;Fp-g为气体与颗粒之间的作用力,方向不确定;Fge为离心力.
1.1.2 气相控制方程
在气固两相DEM模型中,气体的运动规律由N-S方程描述,设εg为气体空隙率,vg为气体表观速度,则气相控制方程为
(2)
(3)
其中,气相控制方程中动量方程的流固耦合项为
Fp=β(vg-vp),
(4)
式中β为气固相间曳力系数,其模型采用Gidaspow曳力模型. 曳力是气固相间最主要的作用力.可以看出,气体对颗粒的曳力Fd与颗粒对气体的力Fp是一对相互作用力.
1.2 接触曳力模型
文中采用DEM模型及支持此模型的仿真软件EDEM软件进行仿真,其提供的颗粒之间的接触模型有Hertz-Mindlin(no slip)模型等[8]. 文中仿真的颗粒都是无黏结性小颗粒,根据实际情况选择Hertz-Mindlin 无滑动接触模型,该模型能高效计算两个颗粒接触时的接触作用力,由法向力和切向力以及滑动摩擦力和滚动摩擦力组成. 法向力分量由Hertzian的接触理论计算,切向力由Middlin-Deresiewicz计算,它们都有阻尼分量,其阻尼系数和恢复系数有关. 库伦摩擦定律决定滑动摩擦力,接触独立定向恒转矩模型决定滚动摩擦力.
在颗粒的运动过程中,颗粒受到来自气体的曳力,而气体又因为颗粒的存在对其流动产生影响,因此两者之间存在紧密的耦合作用,曳力影响了颗粒的输送,因此曳力模型的准确性是非常关键的.
1.3 气固两相耦合
气固两相DEM模型模拟程序由空气流场Fluent计算和颗粒动力学EDEM计算两部分构成,模拟时,颗粒场与空气流场的求解交叉进行. EDEM+Fluent耦合求解过程如图1所示. 在一个时间步长内,Fluent通过UDF和EDEM中的API接口相结合,先在Fluent中进行流场计算,当迭代收敛时,触动EDEM开始当前时步的颗粒计算,并把Fluent中的流场数据传递给EDEM,根据Gidaspow曳力模型计算气体与颗粒间的相互作用力,再根据Hertz-Mindlin(no slip)接触模型用以计算颗粒与颗粒、喂料叶片、螺旋叶片之间的相互作用力,然后,根据牛顿动力学方程给颗粒定位. 当以上步骤在EDEM中完成后,再把气体与颗粒间的作用力反馈回Fluent中,开始新一代的迭代.

图1 EDEM+Fluent软件耦合求解过程Fig.1 Coupling and solving process of EDEM with Fluent
2 喂料叶片曲面
2.1 曲面曲线方程
当颗粒进入喂料头处的窗口时,随着螺旋径向尺寸的逐渐减小,迫使颗粒进入螺旋输送管底部中心附近或洒落在螺旋叶片上,螺旋轴的高速旋转使颗粒向上输送,螺旋挡板沿高度的倾斜有效地防止了颗粒离心作用引起的溅出. 图2是文中研究的喂料头结构图.
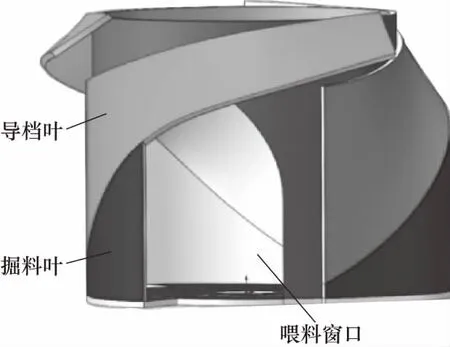
图2 喂料头结构Fig.2 Structure of feeder head
喂料头的输送量由进入的颗粒和流出的颗粒之差组成,颗粒进入的越多,流出的越少,输送量越多,输送量的多少是由螺旋的转速、喂料头的转速和喂料头的结构决定的,而喂料头的结构主要考虑喂料导挡叶的曲面尺寸[8].
利用反向工程,得到某种高效的喂料头的表面数据,并利用这些数据得到了实物原型的三维模型以及喂料曲面的展开图,文中的喂料头的数据都是源于宋斌等[5]、翟晓晨[6]基于反向工程的数据获得的.
喂料头单个导挡叶曲面俯视简图如图3所示.

图3 喂料头单个导挡叶曲面俯视图Fig.3 Sketch for top-view of single feeder surface of guide blade
要拟合的曲线由俯视状态下的点云数据拟合获得,通过测量、分析,在曲线上与中心O的连线达到最大值的点处将边缘曲线分成q1、q2两部分,曲线q1的r值变化较大,曲线q2的r值变化较小,分别对这两部分曲线进行拟合.
以夹角θ为自变量,r为相应的因变量,利用Matlab软件对能够反映导挡叶喂料曲面的特征曲线进行了方程拟合,得到的曲线为一个阿基米德螺旋线,设该曲线为曲线3,曲线方程为r=a+bθ,其中r为极径,θ为极角(弧度).
经拟合后q1的拟合曲线为
r=0.358+0.106θ, 0≤θ<π/3,
(5)
q2的拟合曲线为
r=0.478+0.025θ, 0≤θ≤π/2.
(6)
以上是在喂料口半径为0.358 m时的拟合曲线,其喂料面积和该曲线是成正比的,所以喂料口半径也是和该曲线是成正比的,设置喂料口半径为Rf,则
q1的拟合曲线为
r=Rf+0.3Rfθ, 0≤θ<π/3,
(7)
q2的拟合曲线为
r=1.34Rf+0.07Rfθ, 0≤θ≤π/2.
(8)
当颗粒在喂料叶片中运动时,其有效速度是朝向喂料头中心的速度vn1,它的朝向中心的受力和运动速度由喂料叶片的阿基米德螺旋线决定,而且喂料头的转速不变,颗粒朝向中心的有效速度就不会改变. 根据关系式
t=θ/ωf,
(9)
式中:t为喂料头旋转的时间;θ为喂料头转过的角度(弧度);ωf为喂料头角速度.
颗粒流向喂料头中心的速度为
vnl=(r-a)/t.
(10)
将式(9)(10)联立,并将其简化得
vnl=bωf,
(11)
式中:a,b为阿基米德螺旋线的系数,a为θ=0时的极径;b为每旋转1°时极径的增加量. 从式(11)可以看出,流向中心的有效速度vn1只与螺旋线的参数b和喂料头的转速ωf有关.
下面改变阿基米德螺旋线b的值,观察不同导挡叶曲线的喂料状态. 以渐开线在曲线3的基础上逐渐增大,b分别增大10和20 mm,得到曲线2和曲线1,以渐开线在曲线3的基础上逐渐减小,b分别减小10和20 mm,得到曲线4和曲线5. 即渐开线从大到小分别为曲线1~5. 图4分别为各曲线的q1的曲线图和q2的曲线图.

图4 喂料头导挡叶片各曲线的曲线图Fig.4 Curve graph of all kinds of guide blade of feeder head
因此,导挡叶俯视图的各曲线q1、q2的方程分别为
曲线1:
(12)
曲线2:
(13)
曲线3:
(14)
曲线4:
(15)
曲线5:
(16)
喂料头单个导挡叶左视如图5所示.

图5 单个导挡叶的左视图Fig.5 Left optic of single feeder surface of guide blade
曲线s和曲线m分别为喂料头导挡叶的上下曲线,根据反向工程得到曲线s和曲线m的数据,并进行拟合.
可得s曲线拟合函数为
s=0.000 47θ+0.159.
(17)
式中:θ为喂料头转过的角度;s为曲线s离底端的距离.
可得m曲线拟合函数为
m=-0.000 007 6θ2+0.002 29θ+0.007 35.
(18)
设导挡叶的曲线m和曲线s不变,分别与前面q1、q2的曲线1~5的5个曲线组成不同的5个曲面,下面分析这5个曲面下的导挡叶的喂料头的颗粒情况.
2.2 模型建立
由于喂料头里面的颗粒还受到空气的影响,采用气固两相DEM模型及EDEM+Fluent耦合仿真方法分析喂料头内的颗粒状态. 建立模型,取螺旋管径为0.315 m,喂料口直径为0.34 m,喂料窗口个数3,将上述在Solidwork中建立的模型导入到EDEM软件中,然后再结合Fluent软件进行EDEM+Fluent耦合仿真分析,得到在考虑气体时喂料头内的颗粒状态.
不同时刻的喂料情况如图6所示.

图6 喂料头的喂料过程Fig.6 Feeding states of feeder head
从图6中可以看出,当运行到第2.0 s时,喂料头全部埋入颗粒堆中,颗粒开始沿着螺旋向上输送,此后开始稳定向上输送颗粒. 颗粒在喂料头中的运动轨迹如图7所示.
由图7可以看出,颗粒在喂料头中的运动非常复杂,颗粒的运动速度方向有朝向中心,进入喂料头的;也有离开中心,从喂料头中溅出的. 所以喂料头的输送量由两部分组成,即进入喂料头的颗粒量,溅出喂料头的颗粒量.

图7 颗粒运动轨迹图Fig.7 Movement trace of bulk materials
颗粒与喂料头之间的静摩擦因数是指颗粒与喂料头之间摩擦力与法向正压力的比值,它不仅与喂料头的材料有关,而且与颗粒的表面形状和粗糙度有关,该摩擦因数对喂料头中颗粒的运动状态起很大的作用,所以文中采用不同的静摩擦因数μ进行分析,各种仿真工况如表1所示.

表1 喂料头数值模拟参数表Tab.1 Various simulation working condition of feeding head
如表1所示,分析6种不同静摩擦因数的颗粒的喂料状态,喂料头转速ω分别为10,20,30,40,50,60,70,80,90 r/min,颗粒半径r=2 mm,堆积密度ρ=0.7 t/m3,喂料头转速ωf为0~90 r/min. 螺旋管壁里面的螺旋转速根据文献[12]中的最佳螺旋转速定义得出.
2.3 最佳曲面分析
利用气固两相DEM模型及EDEM+Fluent耦合仿真分析,分别考察以上5种曲面,并比较不同摩擦因数下不同曲面的输送量的对比情况.
当在不同的颗粒与喂料头的摩擦因数下,各曲面在不同转速下的输送量分别如图8所示.
由图8中可以看出,随着颗粒与喂料头摩擦因数的增大,推荐使用渐开线更大些的曲面,因为摩擦因数增大后,颗粒受到喂料叶片的摩擦力越大,颗粒从喂料口溅出量减小,所以曲面渐开线大些好,进料量大,但是曲面渐开线不是越大越好,太大了也容易导致颗粒从喂料口溅出,最大渐开线的曲面1的输送量并不比曲面2大,在任何摩擦因数下都不建议使用曲面1. 同理,随着颗粒与喂料头摩擦因数的减小,推荐使用渐开线更小些的曲面,因为摩擦因数减少后,颗粒受到喂料叶片的摩擦力越小,颗粒从喂料口的溅出量增大,所以曲面渐开线小些好,但是曲面渐开线不是越小越好,太小了颗粒进入喂料口的量减小,所以最小渐开线的曲面5的输送量并不比曲面4大,在任何摩擦因数下都不建议使用曲面5. 不同摩擦因数下推荐使用不同的导挡叶曲面. 当μ≤0.2时,推荐使用曲面4, 当0.2<μ≤0.5时,推荐使用曲面3; 当μ>0.5时,推荐使用曲面2.

图8 不同摩擦因数下的5种曲面的输送量Fig.8 Throughput of five kinds of curve surface in different friction coefficient
3 不同曲线过料面积及输送量计算
3.1 过料面积
由前面颗粒进料的动力学分析,可知
Qt=Qin-Qout,
(19)
式中:Qt为喂料头的输送量;Qin为喂料量,即通过喂料窗户进入喂料头里面的颗粒量;Qout为溅出量,即随着喂料头的转动,从喂料窗口溅出喂料头的颗粒输送量,它与导挡叶的渐开度和颗粒与喂料叶片的摩擦因数有关.
喂料量Qin表示为
Qin=60V,
(20)
式中V为每分钟喂料的体积.
V=2πRfDfnωf,
(21)
式中:Df为喂料口面积;Rf为喂料口半径;n为喂料进口个数;ωf为喂料头转速.
由此可得,喂料头的喂料量为
Qin=120πnDfRfωf,
(22)
单个喂料口的面积Df如图9中的ABCD所示,垂直输送管的结构中心线为DE,q1曲线的终点A点与中心E的连线为AE,连线AD与喂料头的m曲线组成一个截面,该截面被定义为喂料头上的过料面,可近似地认为是一个梯形.
其中,DE为喂料口半径,AE为角度为65°时q1曲线的值,DE和AE之间的角度相差45°,AD的值可由AE和DE求出.BC线段为曲线m上两点之间的线段,B点为角度为60°时曲线m的值,即为梯形中AB的值,C点为角度为120°时曲线m的值,即为梯形中CD的值. 前面已知q曲线、m曲线的方程,从而可求出梯形ABCD中各线段的值,并求出梯形ABCD的面积,即单个喂料面的面积.
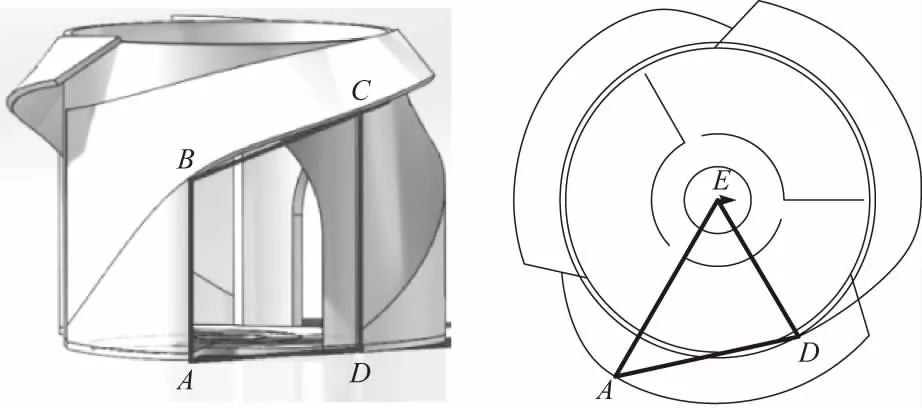
图9 过料面积Fig.9 Single material area
由q1、q2曲线方程(12)~(16)、s曲线方程(17)、m曲线方程(18),可得出不同的5种曲线的过料面积,如表2所示.

表2 各曲线的过料面积Tab.2 Material area of all kinds of curve
3.2 输送量公式
设Qt=kQin,则分别计算不同摩擦因数下的喂料量Qin,并得出不同摩擦因数下的输送量仿真值Qt.
由前面分析可得,当摩擦因数为0.1,0.2时,选择曲面4,并由表3得出喂料面积为0.018 078 m2,当摩擦因数为0.3,0.4,0.5时,选择曲面3,并得出喂料面积为0.018 257 m2,当摩擦因数为0.6时,选择曲面2,并得出喂料面积为0.018 648 m2,然后由式(22),可计算出各喂料头转速下的喂料量Qin,并与前面所得的仿真输送量值进行比较,得到不同摩擦因数下的喂料量与输送量比较图,如图10所示. 由图10可以看出,随着摩擦因数的增大,输送量和喂料量之间的差距越来越小,即颗粒的溅出量随着颗粒与喂料头之间的摩擦因数的增大而减小.
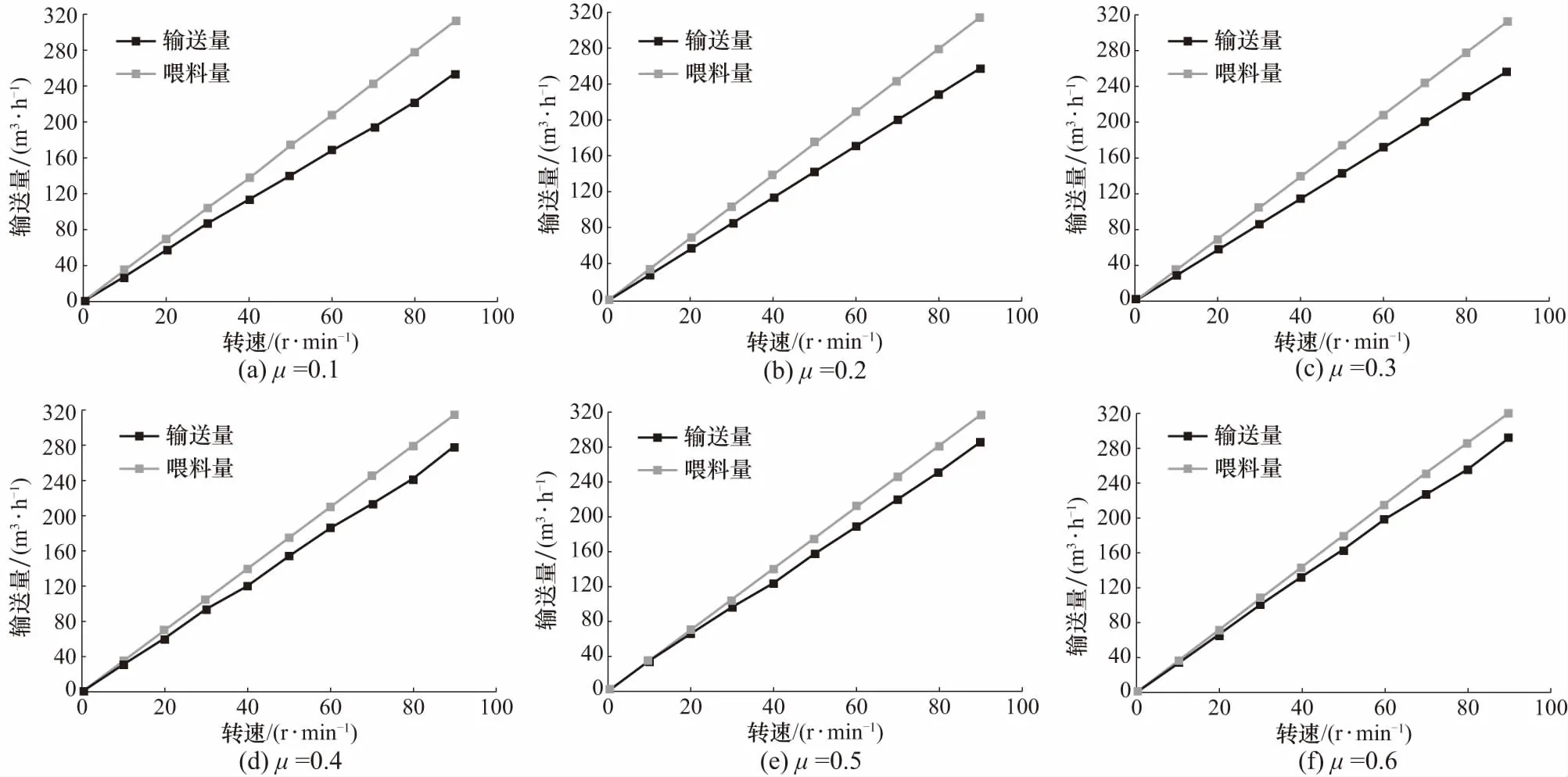
图10 不同摩擦因数下的喂料量与输送量对比图Fig.10 Comparison chart between feeding quantity and transport quantity under different friction coefficient
从式(22)中可得出,在同一摩擦因数和同一曲面下,喂料量和喂料头转速成线性关系,设Qin=aωf,则根据式(22),可得a=120πRfDfn. 从图10中可以看出,输送量和喂料头转速的关系也基本成线性关系,设Qt=bωf,对图13中的每个仿真输送量值进行拟合可得出b. 设k=b/a,则不同摩擦因数下的k便可以计算出,计算结果如图11所示.
拟合函数为
k=-0.075μ2+0.273μ+0.782.
(23)
所以喂料头的输送量为
Qt=(-0.075μ2+0.273μ+0.782)×
(120πnDfRfωf).
(24)
已知垂直螺旋输送机的输送量时,由式(24),可得喂料头的转速为
ωf=
(25)

图11 不同摩擦因数下的k值Fig.11 Value of k under different friction coefficient
4 结 论
针对相对旋转式喂料头进行工作机理研究和动力学分析,分析了其气固两相DEM模型及其仿真方法,以某种高效的喂料头为研究对象,研究喂料头导挡叶5种曲面的曲线方程,并利用EDEM+Fluent耦合仿真方法分析喂料头内的颗粒状态,比较不同摩擦因数下不同曲面的输送量的对比情况,得到不同摩擦因数下推荐使用的喂料头导挡叶曲面. 进行喂料头内输送量和喂料量的分析,计算导挡叶5种曲面的喂料窗口的过料面积,进而推导出喂料头的输送量公式,得到喂料头的转速公式,对喂料头的设计有非常重要的指导意义.

