混沌同步系统降噪方法及其在滚动轴承故障诊断中的应用

李国正， 谭南林， 苏树强， 张驰

(北京交通大学 机械与电子控制工程学院，北京 100044)

当滚动轴承出现故障时，产生的振动信号多以冲击形式出现，其持续时间短、能量频率发散，被大量机械设备的运行噪声淹没[1-2]. 这导致测得振动信号的信噪比非常低，难以获得相应的故障特征频率信号. 因此，需要对测得的振动信号进行预处理，提高信噪比. 混沌类微弱信号检测方法基于非线性系统，是与传统检测技术完全不同的信号处理方法. 它利用混沌系统所具有的初值敏感性、对噪声的免疫性和非线性放大特性完成信号检测，是混沌理论应用于实际工程的重要研究方向之一，具有广阔的应用前景[3-9].

近年来，大量学者对混沌系统的信号检测机理展开了深入的研究，主要集中在：混沌系统检测机理、系统运行状态判定方法、未知频率待测信号测量方法、系统应用与实现方法等方面. 如基于Duffing混沌系统提出了低信噪比下周期信号的频谱感知算法[4]；由相空间轨迹自相关系数判定运行状态变化的方法，并与最大Lyapunov指数法进行了比较[5]；Duffing振子的阵发混沌现象，以此检测未知周期信号的各项参数[6]；研究了结合相空间轨迹方差和遗传算法检测未知频率周期信号的方法[7].

上述研究均采用单一混沌系统来实现，存在效率低、计算量大、易误判、结构复杂、易受元件参数和外部环境影响等问题. 虽然具有高精度、抗强噪声的特性，却无法直接应用于轴承早期故障信号的检测. 考虑到混沌系统之间具有可同步性[8]，本文采用典型Chua电路构建了混沌同步微弱信号检测系统并展开研究.

1 混沌同步系统降噪机理和频率估计

1.1 理论模型和工作机理

新方法适用于检测强噪声背景下微弱周期信号的频率值. 此类微弱信号的信噪比较低，当其信噪比低于-20 dB时，传统检测方法难以检测[9]，其表达式为r(t)=s(t)+n(t). 其中s(t)为正弦信号Asin(ωt+θ)，n(t)为白噪声信号N(0,σ2)，其原理性框图如图1所示.

图1中，检测系统由两个具有相同结构的混沌子系统组成，子系统Ⅰ为驱动端，Ⅱ为响应端. 当待测信号r(t)接入子系统Ⅰ时，二者无法保持同步，出现同步误差. 由于混沌系统的相关特性，待测信号中的微弱正弦信号对相空间运行轨迹的影响远大于白噪声. 所得到的同步误差数据放大微弱正弦信号成分的同时，抑制了噪声信号. 而功率谱密度定义了信号或时间序列的功率随频率的分布，它能够表示频谱分量的单位带宽功率. 本文结合功率谱密度能发现信号中隐含的周期性和谱峰等信息，进行故障特征频率提取和轴承故障早期判定.

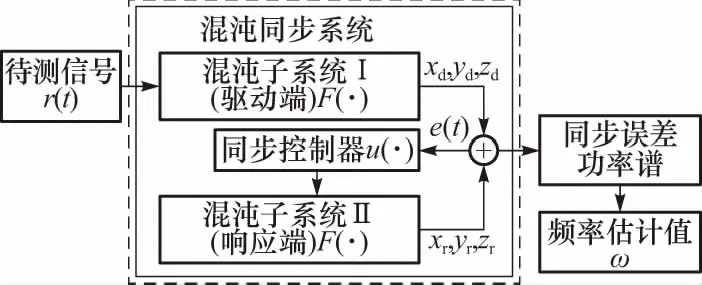
图1 混沌同步检测系统图Fig.1 Detection system via chaotic synchronization

1.2 Chua电路模型及其参数配置

本文基于Chua电路搭建混沌同步频率检测系统，其数学模型为

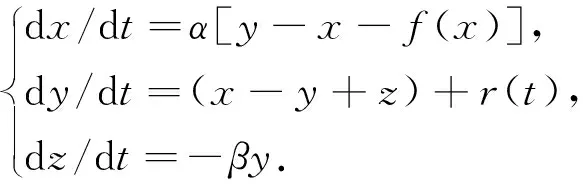
(1)

式中:函数f(x)=m1x+0.5(m0-m1)[|x+1|-|x-1|]，其斜率为m0和m1. 当待测信号r(t)接入时，Chua电路为了一个更高维的动力学系统. 当其参数满足一定条件时，系统进入不同状态. 部分结构参数设定为：β=15，m0=-1.3，m1=-0.6，得到参数α的分岔图，如图2所示.

图2 参数α的分岔图Fig.2 Bifurcation diagram of the parameter α

图中，当参数α≤7.8时，系统进入周期态；当7.8<α≤10.7时进入混沌态；α>10.7时进入发散态. 分析3种状态下不同信号输入对运行轨迹的影响，得到的轨迹如图3所示.

a为无信号输入;b为输入正弦信号; c为强度0.001×sin(2πt)的白噪声输入;d为正弦信号和白噪声叠加输入图3 Chua电路相空间轨迹图Fig.3 Phase space trajectories of Chus circuit

周期态时状态变量的波动范围小，不利于信号的检出；发散态时状态变量迅速增大，无法应用于检测；混沌态时曲线a和c以及b和d的运行轨迹几乎重合. 比较曲线a和b以及c和d，可以看出输入正弦信号后，轨迹发生巨大偏移，且偏移量远超出信号幅值. 可见，混沌态时轨迹放大了周期信号，抑制了噪声信号，轨迹有界，利于检测微弱周期信号.

1.3 Chua电路混沌同步模型

采用自适应的方式搭建Chua电路频率检测系统. 其中混沌子系统Ⅰ的状态方程为

(2)

响应端的混沌子系统Ⅱ的状态方程为

(3)

式中r(t)由正弦信号Asin(ωt)和白噪声n(t)组成，远小于状态变量. 控制器u的表达式为

(4)

式中:ex=xd-xr;ey=yd-yr;ez=zd-zr. 当式中参数k的取值满足条件

α[1+min(m0,m1)+k]>0.

(5)

可以证明，在控制器u的作用下，同步系统的驱动端和响应端在无输入信号扰动时可以保持同步. 为此，构建Lyapunov函数

求导，可以得到

dV(ex,ey,ez)/dt=exe′x+eye′x+eze′x.

(6)

带入式(2)(3)，暂不考虑输入信号r(t)时，可以得到同步误差系统

(7)

Chua电路中的非线性函数f(x)是一个分段连续函数，满足Lipschitz条件，不等式

min(m0,m1)(xd-xr)≤f(xd)-

f(xr)≤max(m0,m1)(xd-xr),

(8)

始终成立. 因此，在区间[min(m0,m1),max(m0,m1)]内一定可以找到一个常数Cm，使式

f(xd)-f(xr)=Cm(xd-xr).

(9)

成立. 式(4)和(9)代入式(7)可得到

(10)

代入式 (6)，得

由于k满足条件(5)，则有-α(1+Cm+k)<0，得到dV(ex,ey,ez)/dt<0. 结合Lyapunov稳定性定理可知，当无外部输入信号时，两端可以同步.

1.4 Chua电路混沌同步模型

为了验证同步系统的作用，将正弦信号0.001sin(2πt)和强度为0.001的白噪声叠加输入，信噪比为Rr(t)=10lg(Ps(t)/Pn(t))=-33 dB，得到输入信号与同步误差的频谱，如图4所示.

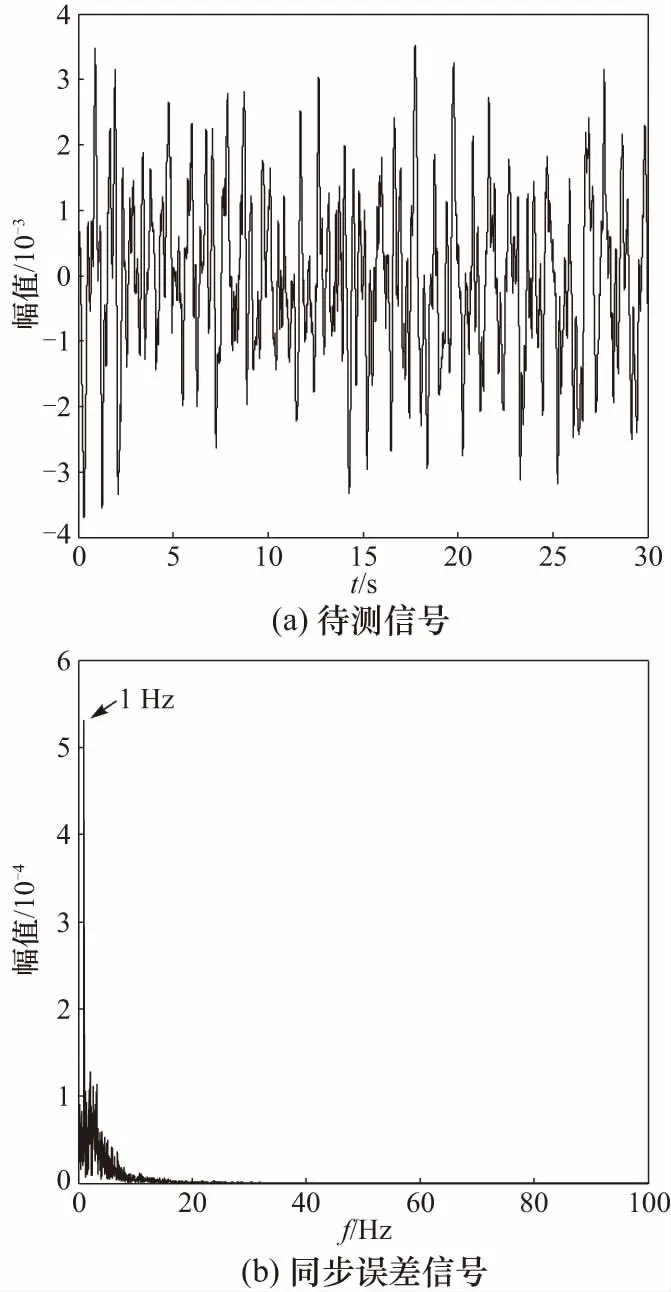
图4 待测信号和同步误差的频谱图Fig.4 The spectrum of the measured signal and the synchronization error

图4(a)中微弱正弦信号的淹没在噪声背景中，在频域空间内难以直接区分. 而图4(b)同步误差频谱图中，大量的噪声被滤除，信噪比达到了-2 dB，可采用频域分析类的方法实现对微弱信号的频率值的估计. 图中得到的频率估计值为f=1 Hz，与实际的正弦信号一致.

2 有效输入区间和方法对比

2.1 幅值与频率的有效输入区间

Chua电路的运行状态还受到输入待测信号的幅值大小和频率的影响，必须进行研究. 保持其结构参数不变，调整输入信号幅值，获取待测信号幅值分岔图，如图5所示.

图5 输入信号幅值的分岔图Fig.5 Bifurcation diagram of the amplitude of the measured signal

图5(a)是输入正弦信号，逐步增加其幅值得到的分岔图.A=0.167是状态转换的临界点. 小于该值时为混沌态，可进行信号检测；图5(b)是在正弦信号中增加白噪声，使信号的信噪比低于-25 dB，并增加正弦信号幅值得到的分岔图. 此时临界点A=0.151. 由此可见，有效输入区间主要是受周期信号幅值的影响，当被测信号幅值不满足要求时，需进行预处理.

进一步分析混沌同步频率检测系统对不同频率正弦信号的作用. 保持被测信号的信噪比不变，改变被测信号中正弦信号的频率值，得到相应的特性曲线，如图6所示.

从图6(a)可以看出，系统状态转换的临界点随着频率的增加逐渐减少，当频率值为45 Hz时临界点最小为0.03. 图6(b)是改变正弦信号频率值后所得到的同步误差的信噪比变化曲线. 可以看出，随着频率变化SNR曲线有一定波动，但在当前区间内，信噪比始终大于-5 dB，可以通过功率谱密度等传统时频域分析方法处理同步误差直接获取信号的频率值.

图6 临界点和SNR曲线Fig.6 The critical point and SNR curve of synchronous error

2.2 方法对比

新提出的频率检测方法与现有混沌类信号检测方法在检测原理和实现方式上并不相同. 为了进一步说明，对比新方法与现有方法[3,7]在混沌模型、测量参数、成本、检测时长等方面的区别，如表1所示.

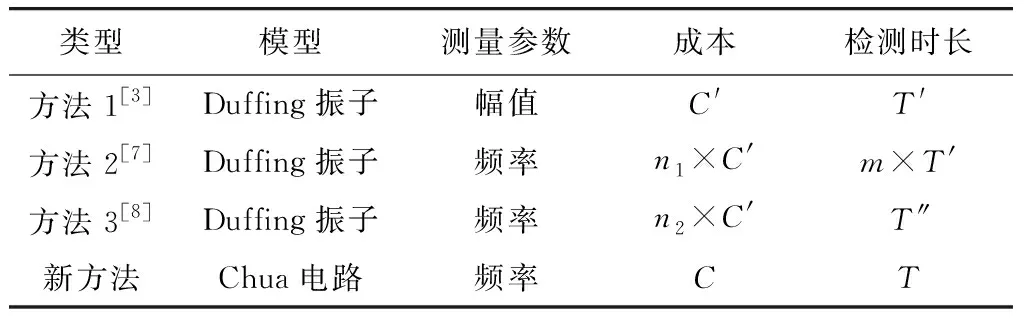
表1 方法对比

从基本检测原理来看，方法1、2和3均需通过参数设定使系统运行在状态转换的临界点，再由系统运行状态的变化实现信号检测. 区别在于方法1检测时仅能测量频率已知的周期信号幅值；方法2是在方法1的基础上结合了优化算法，采用多个Duffing振子系统匹配查找信号的频率值；方法3是在方法1的基础上，结合间歇混沌现象来实现频率估计的方法. 新方法直接从同步误差来实现被测信号的频率估计，与方法2和3采用的多Duffing振子系统相比，结构更简单，成本更低，且无需对状态进行判定，检测时长更短.

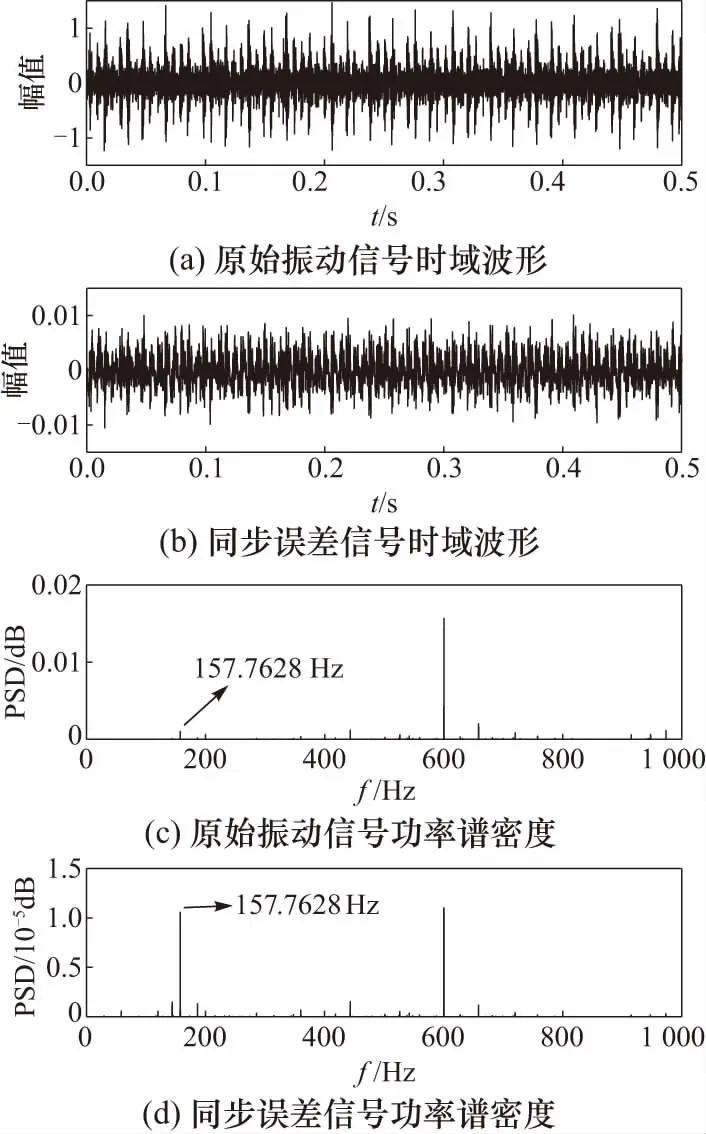
具体来看，方法1基于单个Duffing振子，成本C′为构建系统所需的运算放大器和乘法器，检测时长T′为系统运行状态判定所需要的时间. 若被测信号的频率值为ω，通常情况下T′>6/ω才能完成对系统运行状态的判定. 由方法2的检测原理可知，其构建成本为优化算法初始种群的个体数量n1，为n1×C′，检测时长则为进化的代数m乘以单次检测的时长T′. 种群数量越大，成本越高，检测时长可以缩短. 由方法3的检测原理可知，振子个数n2是覆盖被测频率区间的振子数量. 区间越大，振子数量越多. 构建成本为n2×C′. 间歇混沌现象对系统状态判定的要求更高，通常情况下所需时长T″≫T′. 而新方法中Chua电路结构简单成本C≪C′≪n1×C′≪n2×C′，检测时长取决于对同步数据频域分析所需时长，通常情况下T>4/ω即可实现，有T

3 滚动轴承故障诊断

滚动轴承的局部损伤会引发的冲击，其频率是对应的故障特征频率，该值可以通过轴的转速，尺寸和损伤点的位置加以确定. 采用西储大学实测的滚动轴承振动信号进行检验. 该数据由加速度传感器采集不同部位损伤轴承的振动信号得到，采样频率为12 kHz. 被测轴承为深沟球轴承，其滚动体个数z=9，接触角α=0，参照已有研究可得出内圈、外圈和滚动体出现损伤时，故障特征频率与转速(Hz)之间的系数关系，如表2所示.

表2 故障频率系数表

取内圈存在单点损伤，损伤直径为0.177 8 mm时的振动数据为输入信号，接入上文的混沌同步降噪模型，对该信号和同步误差信号求其功率谱密度，波形如图7所示.

图7 内圈损伤的信号波形图和功率谱密度Fig.7 The power spectral density and waveform of inner ring damage

根据表3和电机转速1 748 r/min，计算得到故障特征频率为fi=157.762 8 Hz. 对比降噪前后的功率谱密度峰值可见，经过处理后，故障特征频率信号被显著放大.

取外圈存在单点损伤时的振动信号进行同样的处理，得到的波形如图8所示.

此时系数为3.584 8，电机转速为1 796 r/min，计算得到故障特征频率fo=107.305 Hz. 图中可见，原始振动信号中的故障冲击信号完全被噪声覆盖，无法发现故障特征频率. 而与之对应，经混沌同步系统降噪后的功率谱密度在故障特征频率处出现了峰值.

取滚动体存在单点损伤时的振动信号进行同样的处理，得到的波形如图9所示.

此时系数为4.713 5，电机转速为1 796 r/min，计算得到故障特征频率fo=141.090 8 Hz. 对比功率谱密度峰值可见，该情况与处理外圈故障振动信号时的结果相似. 由图8和图9可以看出，这两种情况下故障损伤小，冲击信号较弱，其特征频率仍不是功率谱密度幅值的最大值，可以考虑与典型轴承故障诊断的时频域处理方法进一步结合，实现更准确的故障判定.

图8 外圈损伤的信号波形图和功率谱密度Fig.8 The power spectral density and waveform of outer ring damage

图9 滚动体损伤的信号波形图和功率谱密度Fig.9 The power spectral density and waveform of rolling element damage

4 结 论

提出了一种基于混沌同步系统的降噪方法，以Chua电路为基础构建了相关模型，分析了系统的工作机理，并将其与功率谱密度相结合，对滚动轴承的振动信号进行分析和处理. 新方法免于结构参数的精确设定和系统运行状态的复杂求解，提高了适用性. 实验结果表明，将其应用于实际轴承振动数据的去噪处理后，滤除了噪声，使故障特征频率信号更为明显. 新方法可与传统时频域处理方法相结合，形成新的诊断方法，以满足工程应用需要.