组合波片的椭圆率角测量方法

程一斌， 侯俊峰， 王东光

(1.中国科学院 国家天文台，北京 100101; 2.滁州职业技术学院，安徽，滁州 239000)

波片是偏振光学技术中的重要元件，被广泛应用于光通信、激光调谐、遥感、天文及物理学研究等领域[1-3]. 组合波片降低了加工难度，实现了波片的消色差性能，成为偏振测量领域不可或缺的一种波片类型. 但是组合波片在研制过程中存在一个容易被忽视的问题，由于不可避免的加工和装配误差，导致波片中晶体的快轴方位很难完全垂直，使得波片由一个完全理想的线性延迟器变为了椭圆延迟器. 此时，组合波片的偏振性能需由相位延迟、快轴方位和椭圆率角3个参数才能完全描述. 其中，相位延迟和快轴方位的测量方法较多，有机械旋转调制[4-5]、偏振调制技术[6-8]、光弹调制[9-10]、补偿法[11-12]、分频激光探测法[13-14]等. 相比之下，椭圆率角的测量方法少有报道，现有的相位延迟和快轴方位的测量方法均无法有效测量椭圆率角. 然而，椭圆率角的测量对于高精度偏振测量极其重要，尤其当偏振测量精度或仪器定标精度要求优于0.01时，椭圆率角的影响将愈加显著. 因此，如何精确测量组合波片的椭圆率角成为高精度偏振测量面临的新问题.

本文提出了一种基于Mueller矩阵的椭圆率角测量方法. 该方法基于偏振理论和Mueller矩阵分解，建立了组合波片的偏振模型，该偏振模型由相位延迟、快轴方位和椭圆率角3个未知参数完全描述. 通过测量组合波片的Mueller矩阵，利用非线性拟合可同时计算出组合波片的包括椭圆率角在内的3个参数. 本文利用Mueller矩阵椭偏测量系统分别测量并计算了λ/4和λ/2组合零级波片的椭圆率角，结果表明测量方法有效可行. 该方法适用于任意组合波片的椭圆率角测量，应用广泛.

1 基于Mueller矩阵的椭圆率角测量方法

1.1 组合波片偏振模型的建立

Shih-Yau Lu和Russell A. Chipman在1996年提出[15]，任意非奇异Mueller矩阵可以分解为3个矩阵，分别描述减偏、退偏和延迟效应. 其中描述延迟效应的矩阵可用于描述任意组合波片的偏振特性，该矩阵如式(1)(2)所示.

(1)

(mR)ij=δijcosR+aiaj[1-cosR]+

(2)

式中：0表示三元零列矢；R表示相位延迟；δij为Kronecker delta函数；εijk为Levi-Civit置换符号. [1a1a2a3]T表示组合波片快轴的归一化Stokes本征矢量，该矢量描述了组合波片的本征状态. 当a3=0时，本征矢量为线偏振，组合波片为理想的线性延迟器；当a3≠0时，本征矢量为椭圆偏振，组合波片变为椭圆延迟器. 理论可获得本征矢量与组合波片快轴方位和椭圆率角的函数关系，如式(3)所示.

(3)

式中：θ为组合波片的快轴方位角(-π≤θ≤π)；β为椭圆率角(-π/4≤β≤π/4)，综合式(1)～(3)可获得组合波片的Mueller矩阵，如式(4)所示.

(4)

理想情况下，如果组合波片为一个线性延迟器，则β=0. 此时，式(4)简化为式(5)，后者即为常用的理想线性延迟器的Mueller矩阵，由相位延迟和快轴方位两个参数完全描述.

(5)

非理想情况下，由于不可避免的存在加工和装配误差，导致组合波片各晶体之间的快轴方位没有完全平行或垂直. 此时，组合波片由理想线性延迟器变为椭圆延迟器(β≠0)，需要考虑椭圆率角参数. 因此，式(4)为组合波片的通用偏振模型，由相位延迟、快轴方位和椭圆率角的三角函数完全描述.

1.2 椭圆率角测量方法

建立组合波片的偏振模型后，椭圆率角的测量步骤如下.

利用Mueller矩阵椭偏测量系统测量组合波片的Mueller矩阵Mmeas;

建立目标函数F(R,θ,β)=MR-Mmeas；

待定利用非线性最小二乘拟合方法求解函数F(R,θ,β)中的所有未知参数. 拟合函数为

由Matlab库函数lsqcurvefit拟合得到所有未知参数,从而得到椭圆率角β.

1.3 仿真验证

为了验证上述椭圆率角测量方法的有效性，仿真模拟如下.

仿真模拟一个水晶材料的组合零级波片(λ/4@540 nm)，其双折射率Δn=0.009，厚片为d1=1.015 mm，薄片为d2=1.000 mm，假设两块晶体之间的快慢轴对准误差为Δθ=0.5°. 根据偏振传输理论，可计算波片的Mueller矩阵如式(6)所示. 其中，T(Δθ)为旋转矩阵，M1、M2为每块水晶的Mueller矩阵.

M=T(-Δθ)M2(R2)T(Δθ)M1(R1).

(6)

(7)

(8)

(9)

Ri=2πΔndi/λ,i=1,2.

(10)

由式(6)～(10)可获得组合零级波片的Mueller矩阵随波长的变化，如图1所示. 横坐标为波长，单位nm；纵坐标是Mueller矩阵的各个矩阵元，量纲为一. 图中灰线为式(6)～(10)获得的仿真结果，黑线为式(4)获得的拟合结果，可以看出，仿真与拟合的结果是完全一致的. 根据图1的矩阵拟合计算出相位延迟R、快轴方位θ和椭圆率角β随波长变化的结果如图2所示.

图1的仿真结果表明,组合波片的偏振模型是正确的；基于Mueller矩阵的椭圆率角偏振测量方法有效可行.

图1 组合零级波片Mueller矩阵随波长的变化曲线Fig.1 Curves of Mueller matrix with wavelength for air spaced zero-order waveplate

图2的仿真结果表明,组合波片的各晶体之间的快轴方位存在装配误差时，导致最终总的快轴方位角和椭圆率角随波长振荡，且两个参数的振荡幅度基本一致；相位延迟参数随波长变化与快轴方位的装配误差无关.

图2 组合零级波片的偏振参数随波长变化曲线Fig.2 Curves of polarization parameters with wavelength for air spaced zero-order waveplate

2 实验测量和分析

本文作者购买了Thorlabs公司的两个组合零级波片，型号为WPQ05M-532和WPH05M-532，分别对应532 nm的λ/4和λ/2波片，利用Mueller矩阵椭偏仪测量了两个样品的Mueller矩阵，测量结果如图3和图4所示. 其中图3为λ/4波片的Mueller矩阵测量结果，图4为λ/2波片的Mueller矩阵测量结果. 图3和4中，实线为Mueller矩阵椭偏仪的实测结果，一个理想波片的Mueller的第一行和第一列，除第一个元素为1以外，其余元素均为0. 因此，图中实线在这些元素中的非零值代表了Mueller矩阵椭偏仪的测量误差，在0.004范围以内；圆黑色为基于Mueller矩阵的椭圆率测量量方法的计算结果. 拟合计算和实测结果对比表明，两者有很好的一致性，Mueller矩阵拟合误差ΔM在0.004以内. 假设椭圆率角、快轴方位角和相位延迟3个参数相互独立，通过对式(4)在(β=0,θ=0,R=π/2)附近求偏导，可得到椭圆率角、快轴方位角和相位延迟的测量误差δβ、δθ和δR与ΔM之间的关系如下.

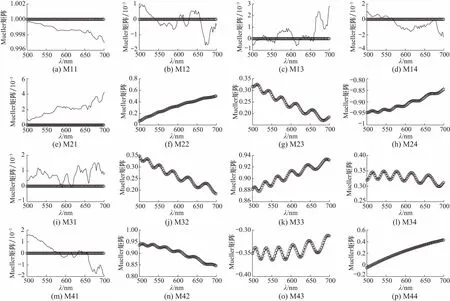
图3 λ/4组合零级波片的Mueller矩阵随波长的变化曲线Fig.3 Curves of Mueller Matrix with wavelength for air spaced zero-order quarter waveplate

图4 λ/2组合零级波片的Mueller矩阵随波长的变化曲线Fig.4 Curves of Mueller Matrix with wavelength for air spaced zero-order half waveplate

(11)

计算表明，椭圆率角、快轴方位角和相位延迟的测量误差分别为0.11°、0.11°和0.22°.

图5和图6为基于Mueller矩阵的椭圆率角测量方法计算获得的相位延迟、快轴方位以及椭圆率角3个参数的测量结果. 计算结果表明：

图5 λ/4组合零级波片的偏振参数测量结果Fig.5 Curves from measurement of air spaced zero-order quarter waveplate

① 相位延迟参数不随波长振荡，与图2的仿真结论一致；

②λ/4的椭圆率角和快轴方位角随波长振荡，振荡幅度一致，约为1°;

③λ/2的椭圆率角和快轴方位角随波长振荡，振荡幅度一致，约为0.4°；

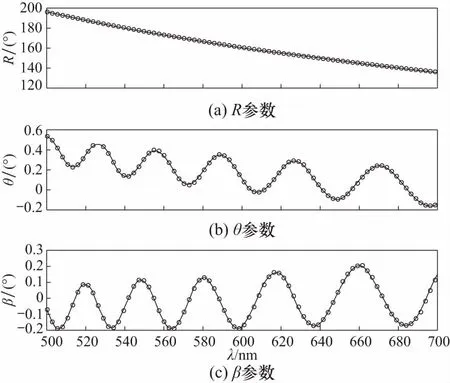
图6 λ/2组合零级波片的偏振参数测量结果Fig.6 Curves from measurement of air spaced zero-order half waveplate

分析结果表明，本文建立的偏振模型可以准确的描述组合波片的偏振特性；而且提出的基于Mueller矩阵的椭圆率角测量方法准确、有效、可行,实测结果和仿真验证结果基本一致.

然而，实测获得的快轴方位角除了随波长振荡以外，还随波长有一定的下降趋势，其中，λ/4的快轴方位角下降约0.2°，λ/2的快轴方位角下降约0.4°，具体原因需待未来进一步深入分析. 但是，该效应不影响椭圆率角的精确测量.

3 结 论

在高精度偏振测量中，椭圆率角是组合波片最重要的偏振参数之一，如何精确测量椭圆率角是精密偏振测量面临的关键问题. 本文提出了一种基于Mueller矩阵的椭圆率角测量方法. 该方法基于偏振理论和Mueller矩阵分解，建立了组合波片的偏振模型，该偏振模型由相位延迟、快轴方位和椭圆率角3个未知参数完全描述. 通过测量组合波片的Mueller矩阵，利用非线性拟合可同时获得组合波片的包括椭圆率角在内的3个参数. 此外，利用偏振传输理论仿真模拟了组合零级波片的Mueller矩阵，验证了该椭圆率测量方法的有效性. 在这些理论基础上，本文利用Mueller矩阵椭偏测量系统分别测量并计算了λ/4和λ/2组合零级波片的椭圆率角，结果表明测量结果与仿真结果一致，测量方法有效可行.

测量计算结果表明基于此方法的拟合误差在0.004以内，椭圆率角和快轴方位角的测量误差为0.11°，相位延迟的测量误差为0.22°. 应用此方法以λ/4和λ/2组合零级波片为样本的测试计算发现其椭圆率角和快轴方位随波长震荡，震荡幅度分别为1° 和0.4°. 本方法适用于任意组合波片的椭圆率角测量，应用范围广.