车辆最佳动力性泛函表达及数值解法
郭智蔷, 吴维, 刘洋, 李博, 苑士华
(1.北京理工大学 机械与车辆学院,车辆传动重点实验室,北京 100081; 2.北京特种车辆研究所,北京 100081)
无级变速传动装置能够实现车辆传动系统速比连续不间断调整,使得任何车速下发动机均能够工作在最佳工况点及高效工作区[1-2]. 通过合理控制无级传动车辆的速比,可以使无级变速车辆具有更好的车辆动力性与燃油经济性,近年来关于无级变速传动装置速比及其变化率的控制策略研究成为车辆研究的热点之一[3-4].
传统的无级变速车辆的最佳动力性速比控制策略由Tsukuda K等提出,控制发动机始终工作在各油门开度下的最大功率点. 罗勇等[5]在此基础上考虑发动机输出特性和无级传动效率特性,以传动系联合输出功率最大为优化目标,采用穷举法得到任意车速和油门开度下的目标速比. 马士泽等[6]提出无级变速速比PID控制方法,经仿真分析后指出速比变化率对加减速性能起着关键性作用,其决定着输出功率和阻力功率的动态匹配关系. 徐少兵等[7]将无级变速传动车辆经济性行驶控制策略的辨识构建为一个Bolza最优控制问题,利用Legendre伪谱最优控制法进行了定量研究,指出最优加速策略是与发动机特性和目标末速度密切相关的动态策略.
泛函分析理论具有高度的抽象性和概括性,近年来泛函分析广泛应用于最优控制问题,但在车辆传动领域应用相对较少[8]. 文中为进一步提高无级变速车辆动力性,实现最佳动力性速比控制,引入泛函分析方法,以目标速比作为泛函宗量,以车辆加速时间作为优化目标构建性能泛函,将车辆最佳动力性速比控制抽象为泛函极值问题. 针对性能泛函强非线性导致无法获得解析解的情况,利用欧拉有限差分法对泛函宗量进行数值求解,得到无级变速传动装置最优加速性能下的目标速比. 通过搭建无级传动系统动态模型,对比分析传统速比控制与泛函优化速比控制下车辆加速性能的差异,验证了泛函分析应用于无级传动装置速比控制问题的理论可行性.
1 车辆加速时间性能泛函构建
车辆的加速时间是表征车辆动力性的重要指标之一,加速性能的优劣直接反应车辆的动力性能. 文中以加速过程中车辆所用的加速时间作为动力性指标,以无级变速速比作为泛函宗量,建立无级传动车辆加速时间性能泛函.
1.1 加速时间性能泛函数学推导
文中所述车辆传动系包括发动机、湿式多片离合器、变速器、主减速器和差速器等. 为保证模型的精确性和简洁性,对车辆动力传动系统进行一定程度的简化:①忽略发动机及变速器高阶动态特性;②忽略由于旋转造成的传动系间隙及相关杆件的扭转变形;③忽略多片离合器车辆加速过程的滑摩[9]. 基于上述假设,对车辆加速时的纵向动力传动过程建模并推导加速时间性能泛函.
在讨论速比控制问题时,假设离合器结合完全同时不发生滑转现象,此时无级变速器输入轴与发动机输出轴可视为刚性联结[7],并且假设车轮滑移率为0,此时发动机转速和车速存在如下关系:
ωe=iCVTim0u/r,
(1)
式中:iCVT为无级变速速比;ωe为发动机转速;im0为主速比;u为车速;r为车轮滚动半径.
无级变速速比iCVT随时间t连续变化,车速u也随时间t连续变化. 速比控制策略在平直路面行驶条件下进行制定,在加速过程中不出现突出的路面阻力,在发动机飞轮转动惯量和无级变速器主动部分惯量较小,且车辆加速响应及时的情况下,车辆加速过程可以保持加速度为正数,即车辆不发生减速,车速u为时间t的单调递增函数. 根据反函数理论,无级变速器速比iCVT可以看作车速u的函数,即:
iCVT(u)=iCVT[t-1(u)],
(2)
将式(1)两端同时对时间t进行求导,得
(3)
考虑发动机旋转部件转动惯量,加速时传动半轴作用于驱动轮的转矩为
(4)
式中:T1为考虑传动效率的驱动轮转矩;Ttq为发动机输出转矩;If为发动机旋转部件转动惯量;ηCVT为无级变速传动效率.
传动系统效率损失由系统中各处接触部件之间的摩擦引起,则传动系中各处摩擦作用转换到驱动轮处的摩擦阻力转矩TR为
(5)
主速比im0为常数,对于变速器速比iCVT的求导等计算不产生影响,因此利用i=im0iCVT进行变量代换,并将式(4)代入式(5),得到传动系统的摩擦损耗功率PR为
PR=
(6)
根据能量守恒定律,得到动力学功率平衡方程
,
(7)
式中:m为整车质量;IW为车轮转动惯量;Ff为滚动阻力;Fw为空气阻力;Fi为坡道阻力.
根据式(7)可以得到车辆加速度av为
(8)
式中:Ft为车辆驱动力;i′为速比相对车速的变化率,即i′=di/du.
根据车辆纵向动力学,加速工况下,车辆驱动力Ft为
Ft=Ttqim0iCVTηCVT/r=TtqiηCVT/r.
(9)
1.2 加速时间性能泛函数学表征
根据车辆加速度的定义可知,车辆的加速时间为加速度倒数对车速u的积分,即
(10)
式中:ta为车辆加速时间;u0、u1分别为车辆的初始车速和终止车速.
根据最简泛函数学形式:
(11)
对加速时间ta的表达作如下变量代换:u=x,i=y,i′=y′,则加速时间ta可视为以车速u为自变量,以目标速比i为宗量函数的泛函,即T=J[i(u)],u0和u1为性能泛函区间端点值.
考虑平坦道路加速行驶工况,坡道阻力为0,并将滚动阻力系数视为常数,对滚动阻力、加速阻力、空气阻力中的计算参数作如下变量代换
λ1=m+∑IW/r2,λ2=If/r2,λ3=fmg,
λ4=3.62CDA/21.15 .
(12)
得到简化后加速时间性能泛函数学表征形式为
J[i(u)]=
(13)
文中取无级传动效率为速比的函数,将无级传动效率拟合为总速比的二次函数,得到无级传动效率数学表达式
ηCVT=p1i2+p2i+p3,
(14)
式中:p1,p2,p3为多项式系数,文中取p1=-0.003 4,p2=0.070 7,p3=0.481 4.
将式(14)带入式(13),得到考虑无级传动效率为变量的加速时间性能泛函式为
(15)
2 性能泛函求解算法及边界条件
文中构建的性能泛函由于其具有强非线性,无法直接利用泛函取极值所满足的欧拉方程获得泛函宗量精确解,文中根据变分法原理,将性能泛函离散化,采用欧拉有限差分法对泛函宗量进行数值求解.
2.1 性能泛函直接解法
对于性能泛函J[i(u)],其边界条件为:i(u0)=i0,i(u1)=i1;利用欧拉有限差分法对泛函宗量i进行数值求解,求解该性能泛函近似解具体步骤如下:
① 将区间[u0,u1]划分为n小段,每个小段称为一个有限单元,每个单元内假设泛函宗量i是自变量u的线性函数,根据Lagrange插值可得
(uk-1≤u≤uk).
(16)
即利用折线代替泛函宗量i(u)解析解中的连续曲线,由于文中性能泛函J[i(u)]只涉及i、i′而不涉及泛函宗量i的高阶导数,因而利用折线近似代替是合理的.
② 将Lagrange插值曲线带入性能泛函,将J[i(u)]转换为节点u1,u2,…,un-1的多元函数,即
J*[i(u)]=φ(u1,u2,…,un-1).
(17)
为保证性能泛函J在各自变量u处均取极值,应使J*[i(u)]在各节点处均达到极值,得到关于节点值的n-1阶非线性方程组
∂φ/∂ik=0 (k=1,2,…,n-1).
(18)
求解式(18)的非线性方程组,可以获得泛函宗量i近似解的一组折线,当有限元尽可能小时,该解可以近似为各车速下的最优加速性目标速比.
2.2 性能泛函离散化
根据欧拉有限差分法,将性能泛函离散化. 泛函宗量在相应点的导数值由导数近似公式计算:
i′k=i′(uk)≈(uk+1-uk)/Δu.
(19)
将性能泛函积分利用矩形公式表示为有限和形式
[f(u0)+f(u0+Δu)+…+f(u1-Δu)]Δu.
(20)
则离散化加速时间性能泛函数值表达式为
为简化计算,取节点差值Δu为定值,在所有节点值处均取得极值,得到关于n-1个节点值的n-1元非线性方程组为
(j=1,2,…,n-1),
(21)
其中,A1~A4具体数学表达式为
式中i0和in分别为车辆加速过程的初、末车速对应的目标速比值.
2.3 泛函边界条件及数值解
车辆加速性能与后备功率密切相关,车辆后备功率大则加速性能好. 将u0和u1的边界条件设置为初始车速和终止车速对应的各油门开度下传动系最大联合输出功率点.
以油门开度α=1为例,为避免出现末端车速过高导致av≈0,造成方程组求解发散的情况(此时1/av≈∞),选取加速过程初始车速u0=6 km/h,末端车速u1=60 km/h,对应变速箱最优速比分别为4.625和0.9,由i=im0iCVT,则边界条件为i0=18.5,in=3.6.
计算过程所采用的系统参数值如表1所示.

表1 系统参数值
为保证离散化结果的精确度及目标速比的连续性,节点数的选取不宜过少. 文中选取节点数为30,根据式(22)的描述得到非线性方程组,利用Newton迭代法进行求解,得到泛函宗量i在不同油门开度、不同车速下的数值解,从而获得最优加速性目标速比.
3 模型动态仿真与分析
为了验证泛函分析法得到的最佳动力性目标速比对于提升车辆动力性的动态效果,建立无级传动系统动态仿真模型,并与传统基于各油门开度下发动机输出功率最大[5]的速比控制策略、联合输出功率最大的速比控制策略进行加速性能的对比分析.
采用油门开度α为1,仿真结果表征车辆的极限加速能力,仿真时采用定步长求解方式,3种无级传动最佳动力性速比控制策略下加速性对比如图1所示. 从图1中可以看出,泛函分析法获得的动力性目标速比在车速由6 km/h加速到60 km/h时所用加速时间最短,为9.1 s;按照联合输出功率最大动力性目标速比加速用时稍长,需要9.2 s;而传统保持发动机工作在各油门开度最大输出功率点的速比控制策略下加速性能表现最差,加速时间为9.9 s,泛函分析法与之相比加速时间减少8.79%.

图1 全油门加速性能对比曲线Fig.1 Contrast curves of extreme acceleration
图2为油门开度为1时,采用不同速比控制策略得到的发动机转速变化曲线. 由图2可知,按照传统的发动机输出功率最大速比控制方法,发动机很快加速到最大功率点转速1 840 r/min并保持不变;而联合输出功率最大法及泛函分析法的末端转速均稍大于最大功率点转速,说明发动机输出功率最大并不能使车辆加速性能最优. 车速在60 km/h之后利用泛函分析法得到的发动机转速有缓慢上升趋势,逐渐偏离联合输出功率最大曲线.

图2 全油门加速时发动机转速曲线Fig.2 Engine speed curves of α=1
图3和图4分别表示全油门加速时车辆加速度和速比变化率曲线. 从图中可以看出,加速过程中车辆加速度一直为正数,未出现车速下降的现象,符合文中目标泛函表达式的建立前提. 发动机输出功率最大法对应的速比变化率负值最大,导致加速度形成两个尖峰且最大加速度较低,加速性能相对较差.
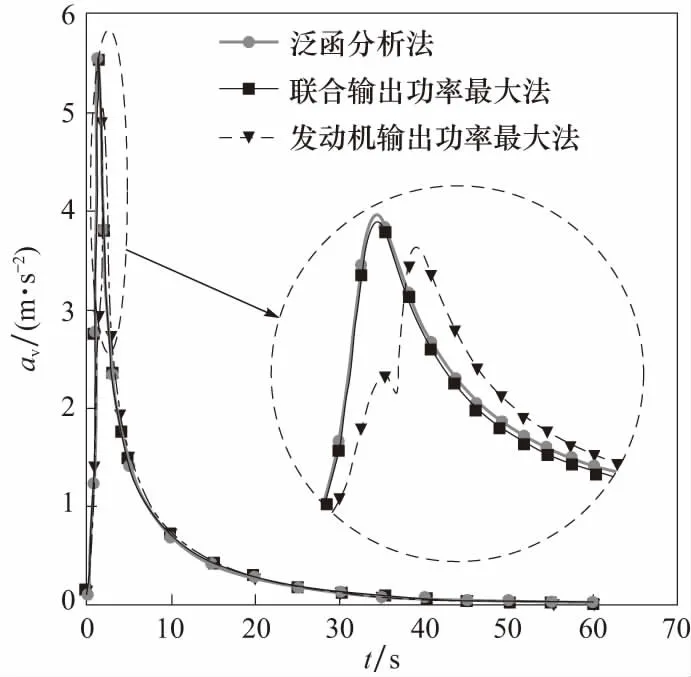
图3 全油门加速时车辆加速度曲线Fig.3 Vehicle acceleration curves of α=1
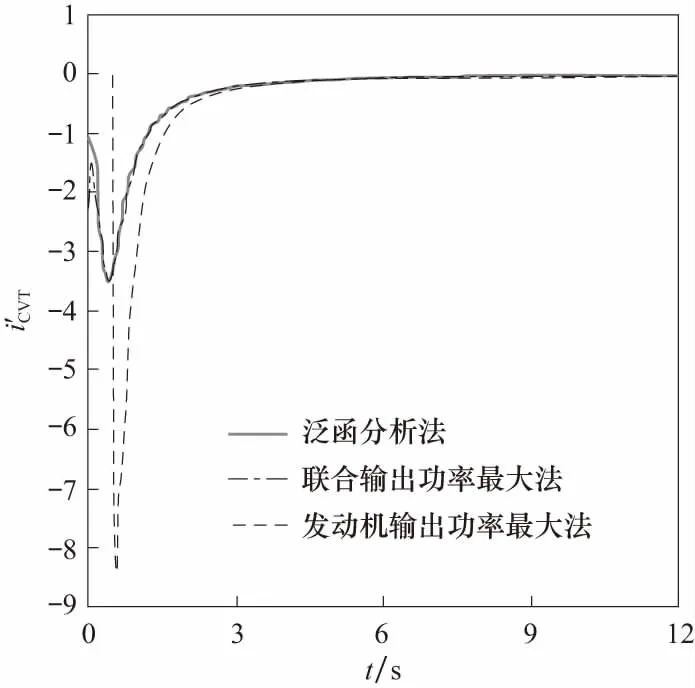
图4 全油门加速时速比变化率曲线Fig.4 Speed ratio change rate curves of α=1
4 结 论
文中将泛函分析理论引入无级变速速比控制问题中,以表征车辆动力性的加速时间作为性能泛函,以变速箱速比iCVT作为泛函宗量,并考虑无级传动效率,构建了具有通用性的车辆加速时间性能泛函数学表征形式.
采用变分法原理和欧拉有限差分法分析以泛函取极值为优化目标的数学问题,对泛函宗量进行数值求解,获得了最佳动力性速比结果,通过仿真对比分析不同速比控制策略下的车辆加速性能,从理论上验证了泛函分析法应用于车辆传动系统最佳动力性速比控制问题的可行性.

