双隐身飞机自卫相干干扰对单脉冲雷达影响

包磊， 王春阳， 白娟， 曾会勇

(1.空军工程大学 研究生院，陕西，西安 710051；2.空军工程大学 防空反导学院，陕西，西安 710051)

信息化作战下隐身飞机不再是单机作战、单打独斗，它会是同种类、不同种类的飞机编队作战，隐身飞机混编协同作战暗示着敌手绝非等闲之辈，主要针对一流的世界空军强国，现如今隐身技术远未达到高度完善的今天，采用机载自卫干扰是保护隐身目标的一种有效手段. 文献[1-2]提出了目标回波与相干干扰共同作用下干扰模型及优化干性比计算方法，为双机编队协同相干干扰设计提供参考思路；文献[3]建立自卫干扰条件下单隐身飞机敏感性模型，分析求解即时动态RCS序列，仿真计算得到飞机在正常飞行与自卫干扰状态雷达探测概率变化情况；文献[4-5]将信干比计算原理与雷达检测概率模型相结合，推导了自卫干扰状态雷达组网检测概率模型并做出相应有效性评估.

然而如何充分有效利用低可检测的隐身优势掩护隐身空袭编队应对单脉冲雷达的威胁，以降低飞机战损率，可采用自卫相干干扰与编队隐身技术相结合，就可使突防飞机实现全航程低损失率的安全突防.

本文借鉴文献[1-4]中针对单脉冲雷达的相干干扰原理与实施手段结合单隐身飞机机载自卫干扰性能模型，利用文献[5-7]中不同航迹下提取的隐身飞机即时动态RCS时变特性思路和相关检测概率模型，评价隐身飞机与雷达检测性能. 并参考文献[8-9]中源于空战特点的双机编队协同作战战术方法与编队协同优势的作战效能评估思路，研究了双隐身飞机协同自卫相干干扰模式对单脉冲雷达角度跟踪、距离测算以及检测性能强弱变化的影响.

1 双隐身飞机协同自卫干扰模型

1.1 场景设计

图1为双隐身飞机编队与机载自卫干扰相结合的应用情况. 图1中，Rmax为单脉冲雷达检测空间目标的最大作用距离；Rj为双机实际自卫干扰的即时距离；θM为单脉冲雷达主瓣宽度. 编队在实施空对地的精确打击同时，为有效保护自身不被雷达检测到，采用双隐身飞机协同自卫式相干干扰，有效诱骗单脉冲雷达角度测量，破坏角度跟踪系统，使雷达跟踪到错误方位.

简化双机空地对抗场景，作战场景如下假设.

① 双机协同飞行航迹在充分考虑雷达烧穿距离，忽略环境外在因素不利影响，采用盘旋飞行进行模拟. 在整体突防过程中，双机编队始终保持统一高度，相同姿态，同一速度.

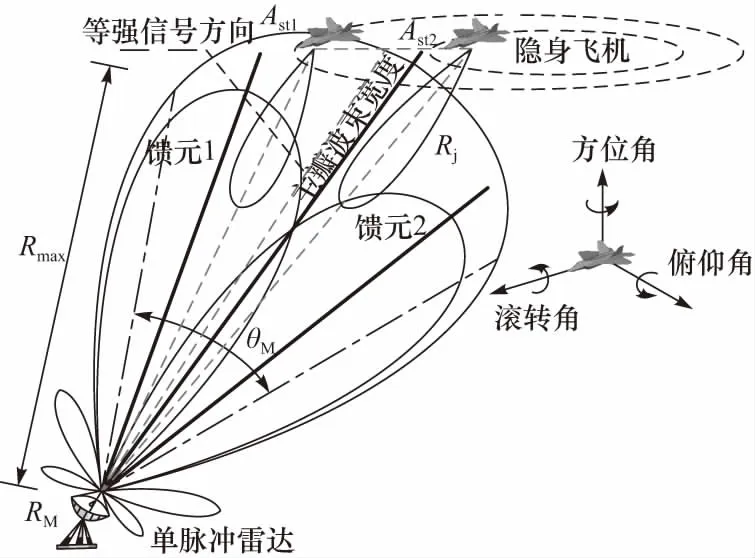
图1 双隐身飞机自卫式相干干扰Fig.1 Self-defense coherent jamming of dual stealth aircraft

② 编队在实施精确打击时，为使隐身效果显著提高，采用相干干扰自卫方式，利用两个相干干扰源同时作用产生合成波，对单脉冲雷达跟踪方位产生错误引导，诱骗产生平台外干扰效果.

1.2 隐身飞机模块

1.2.1 飞机时变姿态分析

隐身飞机的RCS在时空域内随姿态角动态变化，主要表现为：方位角、俯仰角和滚转角构成了反映飞机姿态的三维信息. 目前，通过建立隐身飞机编队航迹并通过相应仿真确定隐身飞机编队的姿态角范围，而后通过二维姿态角实时的变化计算即时RCS的变化值.

1.2.2 即时RCS获取

RCS幅度起伏特性是描述飞行动态过程的重要应用之一，其获取过程包括隐身机动编队目标几何建模、全空域静态RCS数据库建立、编队目标时变姿态角解算、编程提取动态RCS序列4个模块.

1.2.3 隐身机动目标双机编队几何建模

① 编队飞行模型参数设置.

航迹具体设置如下.

双机维持盘旋飞行俯仰角动态范围：-30°<δ<10°，相应滚转角设定为=30°，综合考虑隐身飞机超音速续航能力，简化模型，速度设定一致.

相应双机编队航迹参数设置具体如下.

编队飞行速度1.4Ma；飞行续航高度10 km；隐身飞机st1续航半径35 km；隐身飞机st2续航半径34 km.

依据续航参数绘制图所示双隐身飞机协同支援航迹模型，见图2所示.

图2 双隐身飞机协同支援航迹Fig.2 Cooperative track support by dual stealth aircraft

② 双机体与雷达坐标系设定.

双机体坐标系(O-XstYstZst)：以双机质心连线中心为坐标原点，Xst轴沿垂直机头方向面向西，Yst轴沿平行机头方向，Zst轴垂直机腹方向向下，如图3所示.

图3 双机体与雷达坐标系示意图Fig.3 Schematic diagram of coordinate system of dual airframe and radar

雷达坐标系(O-XMYMZM)：以单脉冲雷达质心为坐标原点O，XM轴沿O所在的纬度线指西，YM轴沿O所在的经度线指北，ZM轴垂直于XMOYM平面，如图3所示. 图3中双机体坐标系中的ε,δ,分别是飞机的方位角、俯仰角和滚转角.

③ 双机体与雷达坐标系转换.

依据战术模型中双机实时位置(俯仰、方位、滚转)参数，在解算对应雷达坐标下编队的即时方位、俯仰与滚转信息，在比对解算得到动态RCS序列. 雷达坐标系下双机即时姿态角解算公式如下[10-13]:

(1)

式中：(xst(t),yst(t),zst(t))对应(x(t),y(t),z(t))在双机体坐标系中等效坐标；(x(t),y(t),z(t))为机体任意一点在单脉冲雷达坐标系中所处方位；(xM(t),yM(t),zM(t))为任一点在机体参考坐标系下坐标.

I为双机体实时坐标与单脉冲雷达实时坐标转换矩阵. 将单脉冲雷达坐标原点(0,0,0)代入式(1)，单脉冲雷达在双机坐标系中的坐标为(xst(t),yst(t),zst(t))，随时间即时变化的方位角ε(t)和俯仰角δ(t)为[11]

(2)

④ 即时动态RCS序列获取.

基于FEKO与Matlab软件仿真设置；俯仰角动态范围：-300<δ<100；相应滚转角设定为=300；方位角设定：00<ε<3600；极化方式：HH(垂直极化)；频率：5.8 GHz；步进间隔：1°.

图4所示双机编队协同以1.4Ma侧盘旋飞行突防行进中，在0～476 s内(即侧盘旋一周)实时动态RCS的仿真结果.

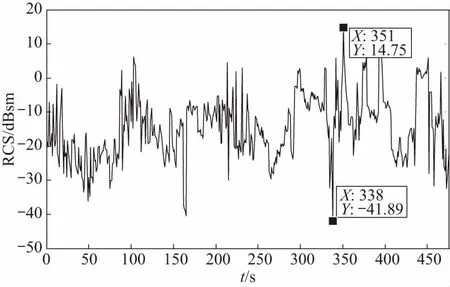
图4 双机队形时变动态RCS序列Fig.4 Time-varying dynamic RCS sequences of dual-aircraft formation

动态RCS序列图形分析：双隐身飞机编队侧盘旋飞行相邻时间动态RCS起伏抖动剧烈、幅度大，规律性不强，浮动范围在-41.89～14.75 dBsm之间. 0 dBsm以上点占比9.24%，总体双机协同隐身效果较好.

2 双机协同相干干扰原理

双机协同相干干扰就是分别由两架飞机携带相位保持一定关系的干扰机产生的干扰. 原理：①雷达依据目标回波的波前法线方向确定目标方位；②双机协同干扰作用产生合成波，信号在雷达天线口面产生波前畸变，使单脉冲雷达跟踪错误方位；③双机干扰信号相位幅度满足相应位置关系时，使单脉冲雷达天线的等信号轴方向跟踪在双机之外，产生诱骗方位角度干扰效果.

根据已建立的双机协同相干干扰模型，截取作战空间态势的一个截面，分析雷达跟踪角度的影响因素.

分析双机在对单脉冲雷达施加相干干扰后雷达跟踪的角度公式如式(4)所示[14]为

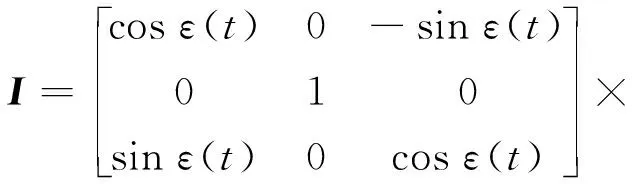
(3)

(4)

式中:ψt为单脉冲雷达跟踪天线指向与等强信号方向实时夹角；η为两隐身飞机干扰功率比；PJ_st1为st1干扰功率；PJ_st2为st2干扰功率；Δθt为双机对雷达两天线即时张角；φ为两干扰信号到天线口面的相位差.

3 单脉冲雷达检测性能模型

3.1 目标回波作用下相干干扰模型

相干干扰相位和目标回波相位在保持相对位置关系时较难，但相干干扰能够产生平台外干扰效果，达到诱骗的效果. 设想等效方法，选用位于双机编队间距方位外的ATr一等效干扰飞机来代替双机编队相干干扰信号，等效设计方法如图5所示.

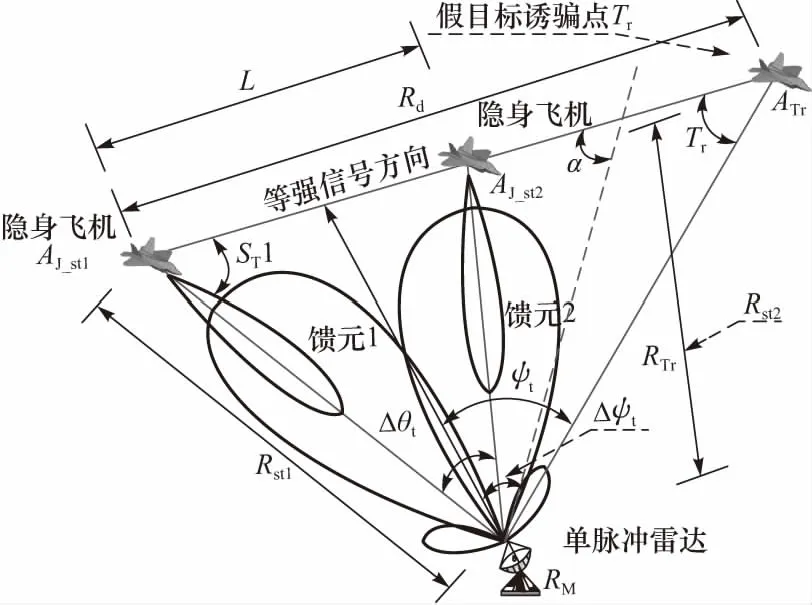
图5 双机协同自卫航迹Fig.5 Cooperative self-defense track of dual-aircraft

等效干扰源功率[1]为

PATr=I0(UJ_st2-UJ_st1)2=

PJ_st2(1+2ηcosφ+η2).

(5)

式中：UJ_st1与UJ_st2分别为雷达两天线接收AJ_st1与AJ_st2干扰信号，假定侧向特性曲线在测角范围内条件为线性，角度跟踪系统采用平方律检波的平衡条件为

PreΔψt=PTr_ j(ψt-Δψt).

(6)

化简为

(7)

式中:Pre为单脉冲雷达接收到相应目标回波信号功率；PTr_j为单脉冲雷达接收到的两相干干扰源的等效干扰功率.

3.2 回波信噪比-功率等效信干比

回波信噪比：对文献[15]雷达检测距离公式变换，推得信噪比计算公式为

(8)

式中:平均发射功率PM=Ptτfr；Pt为雷达发射峰值功率；τ为脉冲宽度；fr为PRF；Gw=Gr，Gw为发射天线增益，Gr为接收天线增益；λ为波长；σst(t)为飞机t时刻的RCS值；波尔兹曼常数k；有效噪声温度Te；接收机带宽Bw；接收机的噪声系数Fw；Lz=LtLf，雷达的积累损失Lt，目标起伏损失Lf；单脉冲雷达即时检测距离Rst(t).

定义回波信号功率与等效干扰功率比值为信干比，即

(9)

式中：PJ_st2，GJ_st2为隐身飞机st2干扰设备功率与增益；Δf为单脉冲雷达接收带宽；Δfj为干扰信号带宽；RTr(t)为单脉冲雷达即时诱偏距离.

令

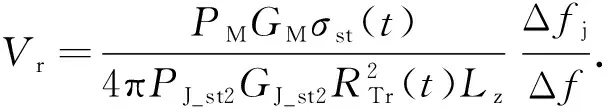
即为目标回波有效信号功率与单脉冲雷达接收到AJ_st2干扰源功率之比.

结合文献[4]推导得出如下公式：

(10)

功率信干比作用下时变雷达跟踪角结合式(7)与式(9)得

(11)

针对平方律检波系统，将式(4)与式(9)带入式(7)可得

(12)

3.3 单脉冲雷达检测概率

(13)

Q函数称为MarcumQ，在Pd相对较大，Pfa较小，UT较大时，提出一个精确近似：

Pd≈

(14)

目标回波+噪声+干扰：针对单脉冲雷达相干干扰对策，将式(10)带入式(14)信噪比(Se/Nwg)，则目标回波+噪声+干扰状态下单脉冲雷达检测概率为

Pd≈0.5×

(15)

4 双机自卫相干干扰效果仿真

4.1 仿真步骤

流程1：利用自卫相干干扰状态下诱偏角度式(4)与式(12)，结合双机编队动态时变RCS序列计算单脉冲雷达诱偏后雷达跟踪角度.

流程2：结合即时编队RCS序列，仿真确定时变信噪比、等效信干比与联合等效信干噪比在0～476 s的具体值.

流程3：依据式(13)与式(15)，结合即时信噪比、等效信干比与联合等效信干噪比，计算编队正常突防状态与自卫相干干扰突防状态下单脉冲雷达检测能力，计算两种飞行状态下时变雷达检测概率并分析相应结论.

4.2 效果分析

4.2.1 雷达跟踪角度

① 雷达参数与干扰设备参数设定.

具体单脉冲雷达参数设置如表1所示.

表1 单脉冲雷达参数设置Tab.1 Radar parameters setting

双机自卫协同干扰的相关仿真参数设置依据如下[16]：①在确保干扰阶段隐身飞机的隐身性能，协同自卫相干干扰达到效果，干扰功率和天线增益设置适当；②覆盖脉冲干扰的干扰频宽采用是雷达接收机带宽的2～5倍；③编队干扰所需信干比通常不大(0～10 dB).

双机干扰参数设置见表2所示.

表2 双机干扰参数设置Tab.2 Jammer parameter setting

② 编队干扰对雷达跟踪角度影响.

释放自卫相干干扰后单脉冲雷达的跟踪角度发生变化，双机干扰源干扰信号到天线口面相位差分别选取(φ=0°，90°，180°). 图6给出了相应双机自卫相干干扰后雷达跟踪角度的实时变化情况.

令干扰功率比η=0.9，对比分析目标回波下跟踪角度的变化规律. 从图6可以看出，干扰诱偏角度与双机编队干扰信号到天线口面相位差φ有关，相位差分别为0°、90°、180°时角度跟踪时变均值为：

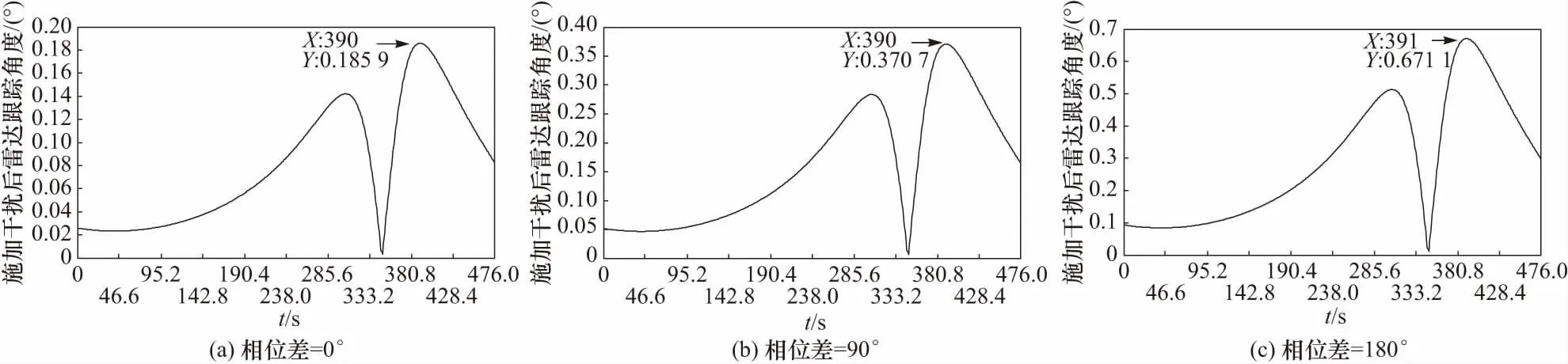
图6 双机自卫相干干扰后雷达跟踪角度Fig.6 Radar tracking angle after self-defense coherent jamming of dual-aircraft

0.07°、0.14°、0.26°. 通过理论推演与仿真求解雷达的诱偏角度最大值条件：双机干扰源干扰信号到天线口面相位差为180°，可见具体实施干扰时，编队飞行双机干扰信号相位相反才能达到最佳干扰效果，能够达到是同向相位雷达角度跟踪误差时变均值的3.71倍.

4.2.2 单脉冲雷达检测概率

在分析编队未释放自卫干扰前信噪比与释放干扰后功率等效信干比变化情况，结合检测模型，求解时变检测概率变化趋势.

① 时变功率信噪比与等效信干比.

双隐身飞机编队侧机盘旋飞行中时变信噪比与等效信干比的即时变化情况如图7所示. 仔细观察时变功率信噪比、等效信干比与(信噪比+等效信干比)实时变化情况与编队即时RCS变化情况基本保持一致. 在无自卫相干干扰下单脉冲雷达信噪比变化范围：-37.65～64.12 dB；在自卫相干干扰下，信干比即时变化范围：-73.14～-2.329 dB；在时变功率信噪比与等效信干比共同作用下，变化范围：-168.4～-5.363 dB. 可见复合的共同作用效果更优，可有效降低等效信干比.

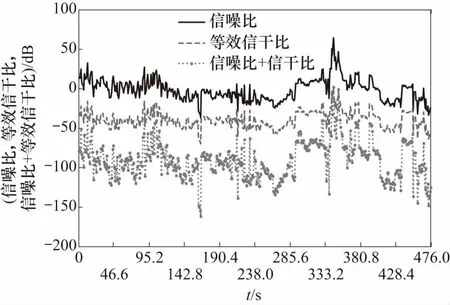
图7 信噪比与功率等效信干比实时变化情况Fig.7 Real-time variation of signal-to-noise ratio and power equivalent signal-to-interference ratio

② 单脉冲雷达时变即时检测概率.

依据虚警概率、信噪比和检测概率的函数关系，设定检测门限：Pfa=10-7，双机编队被单脉冲雷达瞬时检测的概率如图8(a)所示. 时变功率信噪比与单脉冲雷达自身参数有关，干扰设备的干扰效果通过功率等效信干比反映.

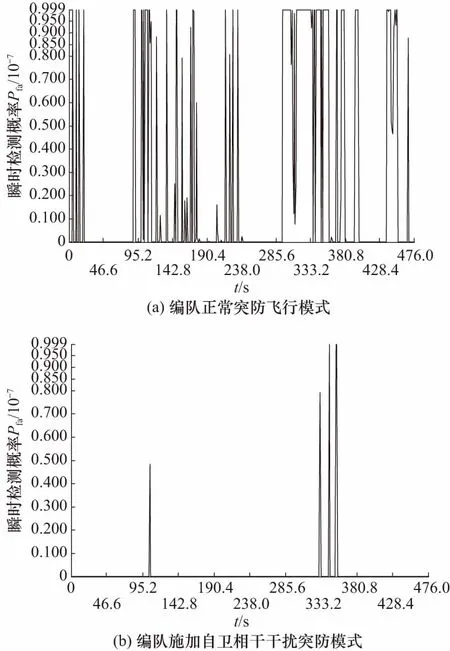
图8 单脉冲雷达时变即时检测概率Fig.8 Instant detection probability of monopulse radar

对比分析图8(a)与图8(b)可得出以下结论：

① 图中所示，隐身编队在0～476 s内被雷达检测发现的概率很大，但检测非连续性，使得跟踪不稳定，但随着累计检测概率的增加，编队面临的突防威胁系数将大大增加. 对比双机编队施加自卫相干干扰模式下，0～476 s内即时检测概率小，即时连续性差，增大了雷达检测概率的即时随机性，大大提高了突防安全概率.

② 对单脉冲雷达实施干扰有很大难度，因为它能从接收的所有回波脉冲中获得跟踪目标的(方位和/或仰角)的全部信息，不是通过比较一串脉冲回波特性来获取信息. 可见自卫干扰应对单脉冲雷达更为困难，突防安全性也面对严重挑战. 通过采用编队自卫式相干干扰思路，双机联合针对单脉冲雷达不可分辨角度范围，破坏角度跟踪系统对目标体或干扰对象的跟踪. 通过仿真表明，对比正常编队突防状态相干干扰利用畸变的相位波前使雷达检测性能下降34.97%，与普通战机相比，结合隐身飞机良好的低可检测能力，使编队突防诱骗效果更加明显，在自卫保护自身突防安全情况下，还可为后续突防战机提供一定空域安全范围.

5 结 论

隐身飞机编队自卫相干干扰是对抗单脉冲雷达检测能力与角度跟踪系统的有效方法. 本文利用隐身飞机的低可检测特性和优越的机动性能，结合设计的编队飞行航迹，在分析单脉冲雷达相应相干干扰原理基础上，根据实际回波信号情况，设计编队干扰方式与构建单脉冲雷达角度跟踪误差与检测性能模型. 利用即时信噪比与功率等效信干比相融合的计算方法结合单脉冲雷达检测概率模型仿真总结自卫相干干扰效果对单脉冲雷达影响.

① 隐身编队自卫相干干扰能够有效诱骗单脉冲雷达跟踪角0.26°.

② 隐身编队自卫相干干扰能够有效使单脉冲雷达检测概率降低34.97%，对比有无自卫干扰状态，在自卫干扰状态，即时检测概率低、呈现零星状态、随机性强、难以形成稳定跟踪状态.

综合分析表明，隐身编队协同自卫相干干扰有效诱骗单脉冲雷达的角度信息并对检测概率、跟踪性能产生很大影响，反映出隐身编队作战实效性与突防生存力更强.