学材再建构：让数学教学更具质感

王月梅

(江苏省海门市城北初级中学 226100)

长期以来，初中生数学学习一直是围绕着教材等固化内容而展开的单向度的学习.这样的学习，难以激发学生学习兴趣.数学学习显得沉闷、单调，学生产生了数学学习疲劳.那么，为什么学生在学习中感受、体验不到应有的激情？笔者认为，一个重要的原因就在于教材中的“结论是预置的”“方法是暗示的”“知识是形式化的”，这样的教材编制，压缩了学生的思维空间、淡化了学生的探究意识、截断了学生的创造源泉.因此，教师在教学中应当进行学材再建构，以便让学生的数学学习更有能效，让教师的教学更具质感.

一、素材重建，让初中数学教学更具探索性

“学材再建构”源于江苏省南通市启秀中学著名特级教师李庾南的“自学·议论·引导”教学法中“重组教材内容，实施单元教学”的思想.实施“学材再建构”，必须以课程标准为准绳、以教材为依托、参照，以学生具体学情为依据，对学生的学习素材(包括显性素材和隐性素材等)进行重建、加工、重组.以便让素材更能适应、促进学生的数学学习，更能助推学生的数学素养的发展.

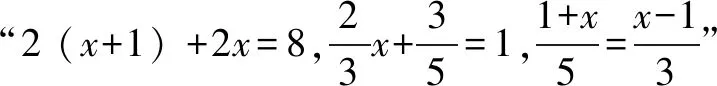
二、方法重塑，让初中数学教学更具开放性

在重建学材的过程中，要遵循学生的认知规律、心理规律等，要从学科知识整体的逻辑视角展开.如此，为学生展开真正的自主、合作、探究学习营建更为广阔的时空.

过去，我们的初中数学教学往往是以知识“点”为媒介，以“课时”为组织单位的，这样的教学容易让学生“见木不见林”.方法重塑，就是要求师生的教学打破以课时、知识点为主的教学模式.以更加统整、更符合学生认知发展的方式、顺序进行教学.在这个过程中，教师要了解学生具体学情，将教学切入学生的“最近发展区”.教学《一元二次方程的解法》，立足于整个单元进行教学，教师要对之进行深度研究.“配方法”“公式法”“因式分解法”“待定系数法”等都是解一元二次方程的有效方法.笔者发现，许多教师都是按教材所介绍方法、顺序，亦步亦趋地展开的.立足于方法的整体视角，笔者认为，教师应当有意识地将“降次”思想贯穿其中.由于“分解因式”能达到降次目的，为此笔者进行方法重塑.将教学顺序调整为“因式分解法”“配方法”“公式法”等，并将之前置，使之成为本单元的起始部分内容.在教学中，力图“未知”与“已知”、“二次”与“一次”、“复杂问题”与“简单问题”的转化，向学生渗透转化、归纳、特殊化、一般化等数学思想.如将方程形式变为(x+m)2=n，运用公式直接将未知化为已知，等等.

常规的《一元二次方程》教学是一种方法一种方法地教、学、练，从而知识整体被分割成碎片.而把握了知识脉络、方法脉络后，教师可以引导学生进行方法重组，从而构建新的学材.这种学材因为关照了数学知识的整体和学生的具体学情，因而具有更好的实践性.通过方法重塑，学生能感受数学的趣味、作用，体会到数学的魅力.

三、结构重组，让初中数学教学更具整体性

初中数学教材往往侧重于数学知识，因此在编排上采用“例题——习题”式的体例结构.在学习中，学生借助反复操练、模仿，就能取得较好的分数.但这样的编排结构，学生容易获得数学知识、形成数学技能，却不利于学生感悟其中内蕴的数学思想方法，不利于学生形成高阶的数学观念，不利于引导学生主动建构、发展学生的创造精神.为了开发数学知识所承载的丰富的数学意识、方法、思想等，我们有必要对学材进行结构性重组.

教学《三角形》，教师不仅要关注三角形的相关知识，更要关注以三角形为基础的其他图形的知识.要主动梳理三角形的相关知识，比如三角形的定义、元素、边的关系、角的关系以及研究三角形的派生内容，如三角形的高、中线、角的平分线、中位线等.有了这样的整体性视角，教师就可以引导学生进行结构性重组，从而让初中数学教学更具整体性、系统性、结构性.首先可以引导学生回忆，唤醒、激活学生已有认知，如三角形的分类、特征、面积公式等.其次引导学生自主建构三角形相关知识，遵循着从“定义”到“相关元素”再到“性质、分类、三角形关系(全等与相似)”的知识形成过程，建构数学知识图.这样的教学，能让学生形成对三角形知识的整体性认知.学生能将新旧知识进行融合、对接，从而连点成线、连线成片、连片成网，进而归纳概括成数学知识的整体板块.

结构性重组，要根据数学知识的特质以及学生的认知特质，具体分析、合理进行.在学材再建构过程中，教师要关注学生的学习基础、能力等，以便让结构重组与学生的学习基础、自学能力同步，让结构重组与学生的认知结构匹配，让结构重组与学生的自主建构、创造同频，让结构重组与学生思维品质、学习力提升和核心素养发展呼应.