初中数学数形结合的应用价值探讨

沈丽蓉

(江苏省海门中学附属学校 226100)

在初中数学教学中，相较于教师将知识灌输给学生，学习思想的渗透更有价值，数形结合便可实现该目标.因此，必须加强初中数学数形结合应用价值的探究.

一、促进初中生形成全面、详细的数学概念

在数学学习过程中，数学概念占据着举足轻重的地位，是其逻辑的起始点，同时在数学教学中占据核心和基础位置.不过，初中数学课本中所包含的数学概念，往往都对其进行高度概括，具有较强抽象性，增大学生记忆和应用等的难度.数学教师在教学过程中，若是所应用的教学方法为数形结合，必定能够真正阐释数学概念.

1.便于学生记忆和理解数学概念

将数形结合应用于实际教学中，能有效转变抽象概念，使其成为更为形象与具体的概念，为学生的记忆和理解提供相应帮助，进而从根本上了解和认知数学概念，最终达到接受这一要求.例如说数轴，教师在进入课堂教学前可以准备好相关工具，包括标尺与称杆等，方便学生在教学中明确这些工具都有三项特点，一是度量起点，二是单位，三是增减方向.通过发挥这三项特征的启发作用，教师将数轴思想传递给学生.针对数轴思想而言，将其度量起点当作直线原点，度量刻度等同直线刻度，增减方向便是直线方向.数形结合势必发挥重要作用，积极转变初中生的数学概念学习过程，从具体模型转变为真正了解和掌握抽象概念.

2.可实现学生数学认知结构的优化

针对数学认知结构而言，以多种数学概念为对象，在学生的思维中实现内化，进而构建起数学思维结构，更加具体来讲，主要是指，在学生的思维中，所形成的数学概念、定理和解题法相互间的关系.对于数学这门学科，学生学习能力有其具体体现，也就是数学认知结构，利用数形结合这一方法能够强化概念与定理等的联系及转化，由此达到数学认知结构优化的目的.比如初中数学中的一元二次不等式，可通过已学的一元二次方程及二次函数图象对其进行讲解.在教学过程中，教师应该使学生明确三者之间的关系，进而提高学生理解与认知一元二次不等式的深度，实现优化数学知识结构的目的.

二、增强学生数学解题能力

1.可帮学生发现最佳解题途径

数形结合着眼于学生思维，在解题过程中，学生利用这一方法能够转换数字符号，使其成为图象，由此发现最佳解题途径.比如，通过应用函数图象解答最值问题.

a和b都是实数，并且a2+b2-4a+6b+11=0，求a2+b2的最大值和最小值.

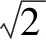
2.可帮助学生简化和缩短思维链条

在题目求解中，学生都会在脑海中形成一条思维链，来源于他们对数学知识的优化与整理.具有较强解题能力的学生，其思维链较为短少，而具有较弱能力的学生，其思维链比较长多，所以利用数形结合可简化和缩短思维链，增强学生的解题能力.

举例来说，在解答几何问题时，若是直线不过圆心，但和圆在AB点相交，此时学生便能形成这一想法，即OA、OC与AC可组成直角三角形，也就是半径与弦心距以及半弦长这三者组成直角三角形，可表示为OA2=AC2+AC2，由此可见，对于圆中的多项问题，通过这一知识模块能将其简化，进而增强学生解题能力.

三、强化学生数学思维能力

1.帮助学生形成形象思维

就形象思维而言，依赖于文字符号，由此形成直观的数学表象，该思维最为突出的特点是必须凭借形象的直观数学文字符号.利用数形结合能够在很大程度上增多学生所掌握的数学文字符号，进一步发展他们的数学形象思维.

例如，当开展反比例函数教学时，某道题为：y=k/x，且k是除零以外的常数.这一函数便是反比例函数，若是自变量是x，函数是y，通过函数图象的分析能够发现：其一，函数图象属于双曲线；其二，如果k大于0，那么双曲线所处的位置是第一象限和第三象限，并且在各象限内x增大的同时y会减小；其三，如果k小于0，那么双曲线所处的位置是第二象限和第四象限，并且在各象限内x增大的同时y也会增大.经由分析可提高学生认知与记忆这三点的深度，印刻在他们的思维中，势必会使学生转换该公式的数学符号，变成形象思维，进一步深化学生对反比例函数的认知.

2.可培养学生发散思维

在数学这门学科中，发散思维主要以同一问题或者是知识点为对象，在分析和研究中，产生各种思路与方法，由此构建起一个思维过程，其终极目标便是探究和发现未知事物，掌握各种解题思路与方法.当开展数学教学时，利用数形结合能够从不同角度设定并提问同一数学问题，进而对学生发挥启发作用，激发他们新的不同类型的解题思维，实现增强学习能力的目的.比如直线与圆的位置关系，学生在判定过程中，通常会对比半径与圆心至直线的距离.不过教师应指出，同样可以应用圆和直线相交的点数，这一方法具有较高复杂度，不过仍旧从一个全新的角度判定了直线和圆的位置关系，以此激发学生发散思维.

在初中数学将教学中，数形结合的应用率较高，本文只是简单分析了该方法在初中数学中的应用价值，还有待加强各方面的探究.总而言之，数形结合这一教学法如果可以发展成具有较强系统性的数学教学模式，势必可以提高教学效率和质量，强化教学效果.