高考立体几何空间角解题技巧
2019-08-26 08:28:56王冬冬
数理化解题研究 2019年22期
王冬冬
(甘肃省静宁县仁大中学 743400)
一、引言及举例
由于空间线面角和面面角是近年高考数学立体几何部分的高频考点,所以本文拟通过典例剖析的形式,具体说明两种常用解题技巧——“几何法”和“空间向量法”.通过不同解法的对比,可以进一步体验:对于同一数学问题,思考的出发点不同,则获得的解题思维也不同,这其中就涉及到解法的优与劣.
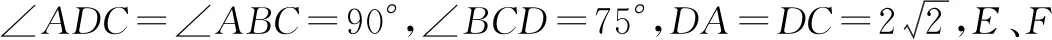
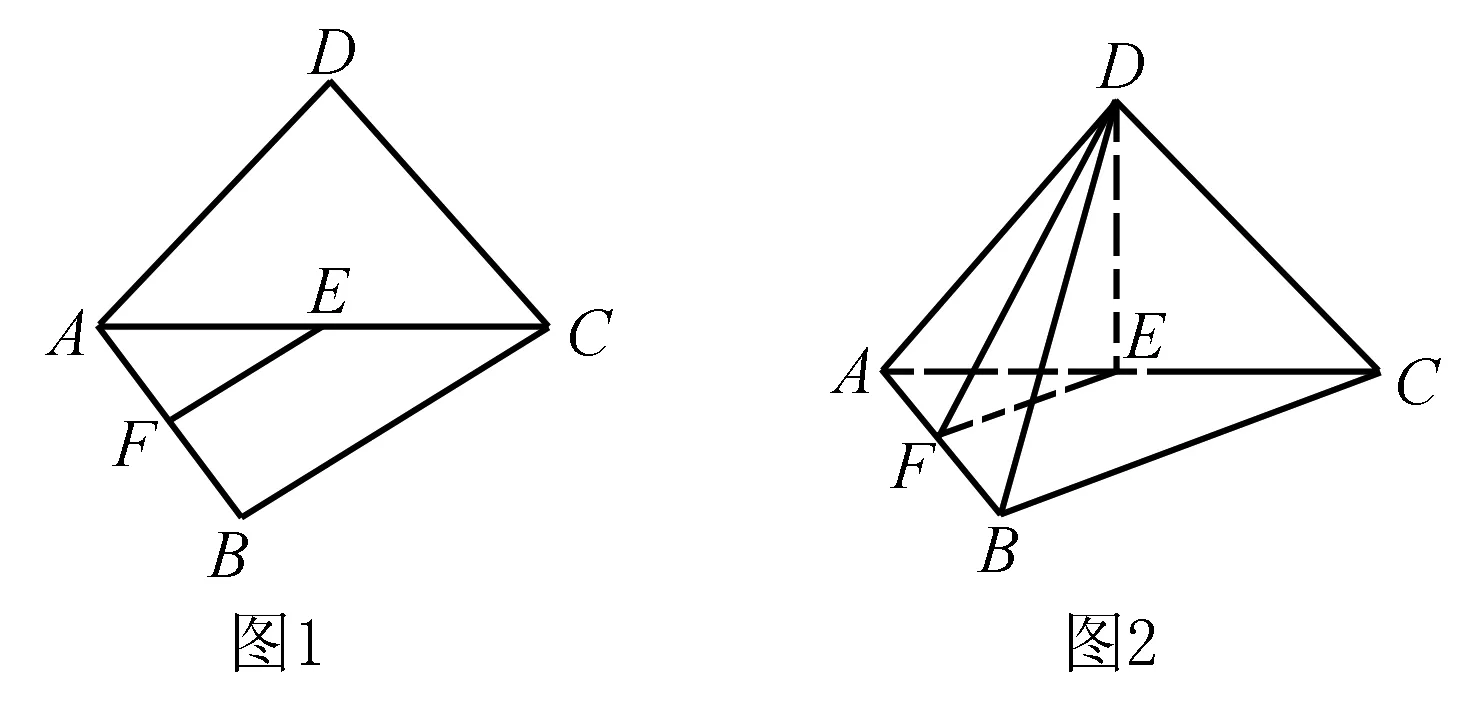
(1)求证:直线AB⊥平面DEF;
(2)求直线BE与平面DAB所成角的正弦值.
好题点睛本题亮点体现在以平面图形的翻折为载体,主要考查立体几何中线面垂直的证明与线面角的求解,体现了近年高考命题的热点,侧重考查考生的空间想象能力、数形结合能力、逻辑推理能力以及运算求解能力.
二、多解探究
1.第一问解法
因为E、F分别是AC、AB的中点,所以EF∥BC.又因为∠ABC=90°,所以可得EF⊥AB.
因为DA=DC,E是AC的中点,所以DE⊥AC.又因为平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,DE⊂平面ADC,所以DE⊥平面ABC,所以DE⊥AB.
又因为EF∩DE=E,故由直线与平面垂直的判定定理得直线AB⊥平面DEF.
2.第二问解法一:几何法
作EO⊥DF,垂足为O,连接OB,由(Ⅰ)可知AB⊥平面DEF,又EO⊂平面DEF,可得AB⊥EO,又DF∩AB=F,所以EO⊥平面DAB,则直线BE与平面DAB内的射影为OB,所以∠OBE就是直线BE与平面DAB所成的角.
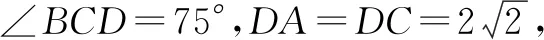

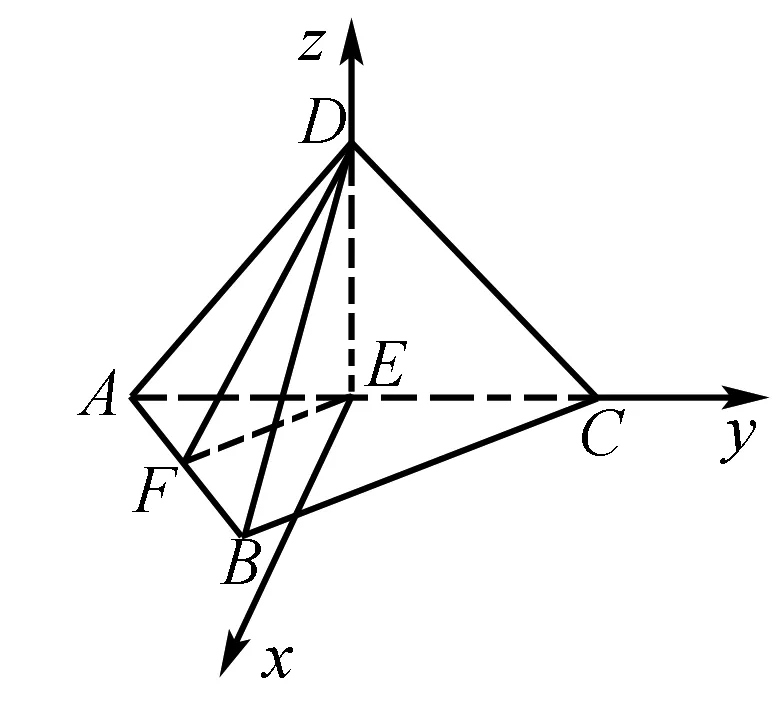
图3
3.第二问解法二:空间向量法
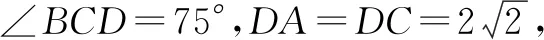
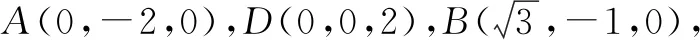
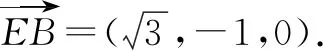
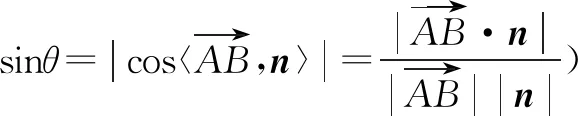
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26 14:05:02
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26 14:00:02
云南化工(2021年10期)2021-12-21 07:33:32
广东教育·高中(2021年11期)2021-12-01 11:58:56
中学生数理化(高中版.高考数学)(2021年4期)2021-07-20 07:18:06
甘肃教育(2020年6期)2020-09-11 07:45:56
活力(2019年21期)2019-04-01 12:17:54
学苑创造·C版(2018年3期)2018-05-28 12:28:00
试题与研究·高考数学(2016年4期)2017-03-28 15:10:19
数学学习与研究(2016年1期)2016-07-04 14:54:19

