探究(An+B)·qn型数列前n项和的求法
王兰灵
(广东省广州大学附属中学 510006)
设数列{an}为等差数列,数列{bn}为等比数列,则数列cn=an·bn可以化为cn=(An+B)qn的形式,为了方便,我们不妨称之为差比数列.差比数列的求和是数列模块的重难点,常用的方法是错位相减法、裂项相消法和待定系数法.笔者在教学中发现求差比数列的前n项和,除以上三种方法外,还可以用导数去解决.本文先对常用的三种方法进行系统地分析,提出了一些便于操作的方法技巧,最后再探究导数解法,供读者参考.



两式相减,得:


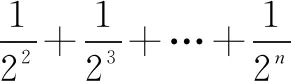
解法2(裂项相消法)设存在常数x、y使得:


将解法2推广到一般情况,对于差比数列(An+B)·qn(其中A、B、q为常数,且q≠0,q≠1),必然存在常数x、y使得(An+B)·qn=[x(n-1)+y]·qn-1-(xn+y)·qn,证明方法与上题类似,计算等式右边,再结合代数恒等式即可求得x、y的值.通常,当0
点评裂项相消法的关键是把差比数列的通项公式正确裂项,所以,记住裂项公式f(A,B,n)=f(x,y,(n-1))-f(x,y,n)或f(A,B,n)=f(x,y,(n+1))-f(x,y,n)尤为重要.从计算量而言,裂项相消法略小于错位相减法,故裂项相消法的正确率会略高于错位相减法.

差比数列前n项和公式的证明:
已知数列{an}的通项公式是an=(an+b)·qn-1,求数列{an}的前n项和Sn.
Sn=(a+b)×1+(2a+b)×q+(3a+b)×q2+…+((n-1)a+b)·qn-2+(na+b)×qn-1①,
qSn=(a+b)×q+(2a+b)×q2+(3a+b)×q3+…+((n-1)a+b)·qn-1+(na+b)×qn②.

点评待定系数法公式属于错位相减法的衍生形式,需要学生熟记该公式,计算量相对较小,有计算便捷的优势,适合做选择和填空等小题目,不大适合做解答题.
解法4(导数法) 在解原例题之前,我们先看一个更为简单的例子,求数列an=n·2n-1(n∈N+)的前n项和Tn.





导数法是否适合一般的差比数列求和呢?答案是肯定的,简单证明如下:
设数列{an}为首项a1,公差为d的等差数列,数列{bn}为首项是b1,公比为q(q≠1)的等比数列为,且cn=an·bn,Sn是数列{cn}的前n项和,求Sn.
解由题意得an=a1+(n-1)d,bn=b1qn-1(q≠1)

在求差比数列前n项和Sn的时候,我们可以根据题型选择解题方法.选择填空题,我们可以选择待定系数法,解答题我们有错位相减法、裂项相消法和导数法可以选择.导数法虽然不常见,但是它用函数思想解决了数列问题,体现了函数的工具价值.我们在教学过程中,不能仅仅满足于现有的教学成果,更要注重知识的联系和拓展,多鼓励学生大胆猜想结论和方法,引导他们亲历从猜想到论证的探究过程,由此发展学生的探究能力和逻辑推理能力,同时也为我们的教学带来更多的精彩.《学记》有言:“学然后知不足,教然后知困.知不足,然后能自反也;知困,然后能自强也.”学生常反思学习,可发现不足,激发求学动力;教师常反思教学,可以取得新的突破,提升教学能力.

