潜射导弹水中无控段弹道散布影响因素分析

李金帅，李向林

(北京电子工程总体研究所，北京 100854)

0 引言

潜射导弹由潜艇鱼雷发射管水平发射，出管后靠惯性向前运动，一段时间后水下发动机启动，控制系统正常工作。启控点的弹道散布直接影响控制系统设计难度。潜射导弹初始无控段弹道散布受诸多因素的影响，包括初始运动学参数、水动力系数、弹体参数、海流和波浪等[1-3]。如果采用单因子变量法研究如此多因素，需要计算大量弹道，而且不便于比较各因素对散布影响的程度，因此本文设计正交模拟试验，分析并比较各因素影响的显著性[4]。

正交试验设计法从全面实验的样本点中找出具有代表性的样本点做实验，从而用较少的实验次数确定各因素的显著性，并找出各因素的最优搭配，已经广泛应用于弹道参数优化。张燚[5]等使用正交试验设计法研究了弹道修正弹末段弹道，分析了影响飞行稳定性和命中精度的主要因素；葛晖[6]等使用正交设计实验研究了潜射导弹运载器分离体下沉弹道，比较了分离体初始运动学参数对弹道散布影响的显著性；蔡群[7]等在文献[6]的基础上，同时考虑了鳍舵、浮质心距，比较了不同方面因素影响的显著性；向谦楠[8]对弹道精度影响因素进行了正交试验设计分析，第1步研究各因素单独作用的显著性，第2步考虑了各因素间可能的交互作用。

本文针对水平发射的潜射导弹出筒后初始无控段弹道散布设计正交试验，分析了不同方面因素对位移散布和姿态角散布影响的显著性，并且对主要因素参数给出了优化建议。

1 水下航行体初始弹道模型

1.1 坐标系定义

地面坐标系：坐标原点O0选在海平面上某点；O0x轴取为射击面与水平面的交线，与射击方向同向；O0y轴铅垂向上；O0z轴按右手螺旋法则确定。

弹体坐标系：原点O取在导弹浮心上；Ox1与体纵轴重合，指向头部为正；Oy1轴位于体纵向对称面内与Ox1轴垂直，指向上为正；Oz1按右手螺旋法则确定。

速度坐标系：原点O取在导弹的浮心上；Ox3轴与导弹速度矢量v重合；Oy3轴位于弹体纵向对称面内且垂直于Ox3轴，指向上为正；Oz3轴按右手螺旋法则确定。

坐标系间的夹角定义与文献[9]相同。

1.2 运动学方程组

根据动量定理和动量矩定理，建立轴对称导弹水下运动方程组[10-12]：

(1)

式中：vx，vy，vz为导弹浮心速度在弹体系下的分量；ωx，ωy，ωz为导弹转动角速度在弹体系下的分量。

导弹平移运动方程组：

(2)

导弹转动运动学方程组：

(3)

式中：ψ,ϑ,γ分别为导弹偏航角、俯仰角、滚转角。

攻角α、侧滑角β及速度v计算如下：

(4)

2 初始弹道散布影响因素及评价指标

2.1 影响因素分析

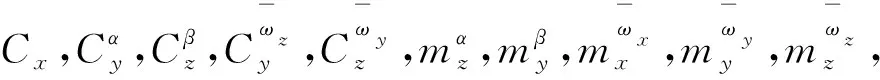
2.2 评价指标

为了描述散布情况，以无拉偏各因素标称值计算得到的弹道为标准，各条件下计算的位移、姿态角终值与标准弹道对应值的差为评价指标，研究上述因素对指标影响的程度和显著性。

3 正交试验设计

正交试验设计是利用“正交表”进行科学安排与分析多因素试验的方法[13]。它可以在很多试验方案中挑选出代表性强的少数方案，并通过对这少数试验方案试验结果的分析，推断出最优方案，甚至得出比试验结果还要多的因素信息。

3.1 影响因素及其水平

2.1节已经讨论了影响因素，同时考虑其他未列入因素，便于进行方差分析，需要插入误差列，共计29列。每个因素都设置3个水平，2水平为参考值，1，3水平为拉偏值。参数拉偏程度主要由设计师常年积累经验确定，同时考虑安全性，通常会比当前技术水平、测量计算精度范围稍大。参考文献[5-8]拉偏程度，本文选取各因素拉偏情况如表1所示[14-15]。

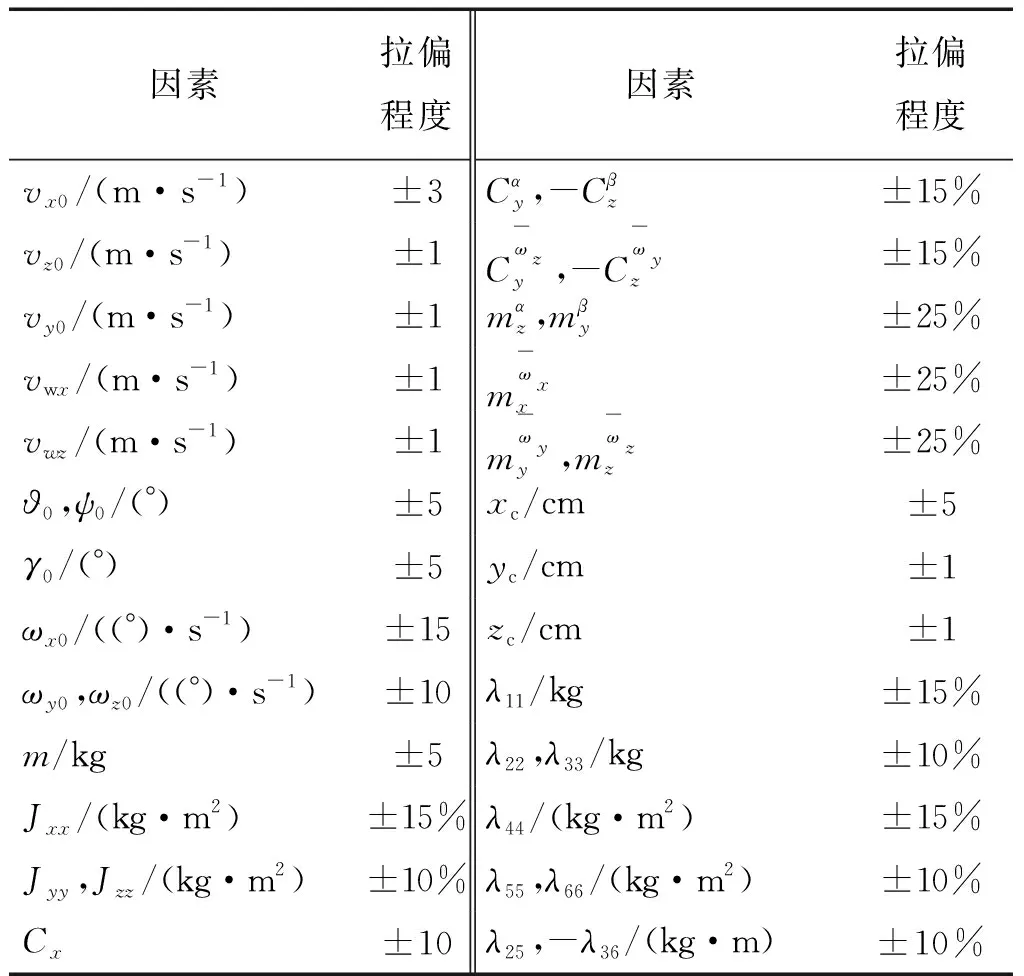
表1 各因素拉偏程度Table 1 Factors and variation range

3.2 正交试验表获取

本文研究影响因素较多，不能从常用正交试验表里直接获取，但是可以用SPSS软件生成。生成时注意加入空白因素列，暂不考虑因素间的交互作用。本文用SPSS生成30因素3水平正交表，任意选择其中29列以供使用。正交表部分如表2所示。

表2 正交试验表Table 2 Orthogonal test table

3.3 试验结果获取及预处理

按试验序号带入对应因素参数进行弹道计算，并将弹道终点的Yf,Zf,ϑf,ψf,γf与标准弹道对应值求差，以便进行后续数据处理。

3.4 极差分析

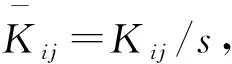
(5)

3.5 方差分析

方差分析可以对影响试验结果各因素重要程度给出精确的数量估计，同时可以提供一个标准考察、判断因素对试验结果的影响是否显著。

设总试验次数为n，因素数为t,每个因素的水平数为r,各次试验结果为ym，则有n=rs。多因素方差分析步骤如下：

(1) 计算偏差平方和ST

(6)

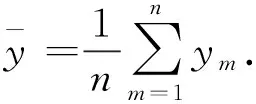
(2) 计算各因素j离差平方和Sj及自由度fj

(7)

fj=r-1.

(3) 计算误差平方和Se及其自由度fe

(8)

(9)

(4) 计算F比，确定拒绝域W

(10)

W={Fj>F1-α(fj,fe)}.

(11)

检验水平α一般取为0.10，0.05，0.01，则显著性对应关系为

(12)

4 仿真分析

本文使用Matlab编程进行弹道仿真，计算工况为水下100 m水平发射，初始速度为13 m/s，x向、z向洋流均为0.2 m/s，无控段时长0.5 s。计算结果导入Excel并按上述公式处理。查表可得F0.9(2,24)，F0.95(2,24)，F0.99(2,24)分别为2.54，3.40，5.61。由于因素较多，方差分析只给出对指标有显著影响因素的数据,极差分析因素数比方差分析多1个。

4.1 y,z向位移

结果如表3～6所示。

表3 y向位移极差分析Table 3 Range analysis of y-displacement m

表4 y向位移方差分析Table 4 Variance analysis of y-displacement

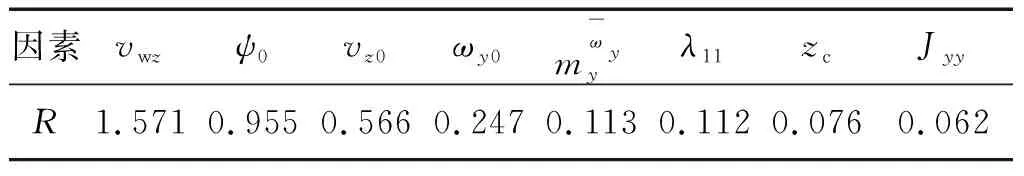
表5 z向位移极差分析Table 5 Range analysis of z-displacement m

表6 z向位移方差分析Table 6 Variance analysis of z-displacement

从表3，5可以看出，在表1所列参数的拉偏条件下，对初始弹道y向和z向位移影响较大的是导弹的初始运动参数，次之的是弹体参数。在相同拉偏程度的情况下，海流对导弹z向位移的影响比速度vz0的影响大，就单位速度引起的z向位移而言，前者约是后者的3倍。另外，表4和表6中都出现了滚转通道参数，说明弹体的滚转也会对y,z向位移产生显著影响。

4.2 姿态角终值ϑf,ψf,γf

结果如表7～12所示。

表7 俯仰角终值极差分析Table 7 Range analysis of pitch angle rad

表8 俯仰角终值方差分析Table 8 Variance analysis of pitch angle

表9 偏航角终值极差分析Table 9 Range analysis of yaw angle rad

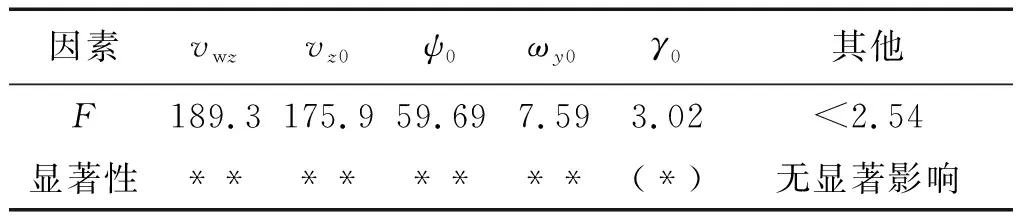
表10 偏航角终值方差分析Table 10 Variance analysis of yaw angle

终值姿态角的极差表中单位均为弧度(rad)。从表7～12可以看出，对俯仰角和偏航角终值影响较大的仍是海流速度和初始运动学参数，弹体参数次之；对滚转角影响显著的是弹体参数和初始运动参数。水动力系数对姿态角终值影响都不显著。

表11 滚转角终值极差分析Table 11 Range analysis of roll angle rad

表12 滚转角终值方差分析Table 12 Variance analysis of roll angle

5 结束语

本文设计正交试验对水下航行体初始无控弹道散布进行了极差分析和方差分析。研究了初始运动参数、弹体参数、水动力系数、海流4个方面共28个因素的影响。在表1参数及拉偏条件下，结果表明,引起位移及俯仰角和偏航角散布的主要因素是海流速度、导弹初始速度和姿态角，引起滚转角散布的主要因素是弹体浮质心距zc，水动力系数仅对z向位移散布产生显著影响。因此，将导弹发射出筒后横向速度、姿态角及姿态角速度限制在较小的范围内，是减小启控点位移散布和姿态角散布的有效途径；缩短浮质心距zc能够有效减小导弹在启控点的滚转角。实验结果对初始弹道位移和姿态优化具有一定参考价值。