无人机任务规划约束空间建模
李文广,胡永江,孙世宇,李建增,褚丽娜
(陆军工程大学 石家庄校区,河北 石家庄 050003)
0 引言
无人机任务规划是根据无人机所要完成的任务、无人机数量及任务载荷的不同,对无人机完成具体作战任务的预先设定与统筹管理[1]。其主要目标是依据战场环境信息,综合考虑无人机性能、威胁及空域管制等约束条件,为无人机规划出一条或多条从起始点到目标点最优或者次优的航路,并确定载荷的配置、使用及测控链路的工作计划[2]。任务规划约束空间就是战场环境要素、链路要素、载荷要素以及无人机性能要素构成的集合,与航迹规划、效能评估等内容密不可分,是任务规划不可或缺的部分。所以对约束空间建模进行研究具有重要意义。
在约束空间建模方面,学者们做了大量工作:曾国奇[3]等人将航迹规划的约束条件分为3类,并分析了各类约束条件模型。但是对各类约束条件模型的研究并不完善。辛培源[4]等人提出了空间综合威胁体的概念,包括探测威胁、火力威胁等。但是约束空间不仅仅是威胁模型,仍需考虑其他规划要素对于任务规划的约束作用。闫云斌[5]等人系统性分析了无人机数据链的各类干扰模型并建立了无人机数据链抗干扰性能评估指标及其测试方法,但忽视了数据链的通视状况对于无人机飞行安全的影响。张民强[6]等人根据建立的传感器模型,制定多无人机对目标的搜索策略,但仅仅依据传感器与目标的欧氏距离以及飞行高度建立的传感器模型很难符合实际任务要求。
上述文献针对约束空间建模展开了一定研究,但存在约束空间建模不够完善以及缺乏系统性梳理的问题。本文将对任务规划约束空间的各类约束模型展开系统性研究,并研究各类模型之间以及模型与任务规划之间的耦合关系。
1 战场威胁建模
实战条件下的无人机任务规划要考虑敌方威胁对无人机飞行安全的影响。根据无人机与敌方雷达、高炮、导弹等威胁之间的相对位置关系,以及威胁的作用范围,计算某位置下无人机被击落的概率,从而在规划航迹时制定相应的避让策略[7]。本文研究建立了探测威胁(雷达)、火力威胁(高炮)、导弹威胁3类典型陆战场威胁模型,可用于描述陆战场威胁对于无人机飞行安全的影响,符合战场实际环境要求。
1.1 探测威胁建模
雷达探测范围如图1所示。

图1 雷达探测范围Fig.1 Radar detection range
根据雷达方程[8]可知:
(1)
式中:Rmax为作用距离;Pt为雷达发射功率;Ae为天线有效接收面积;σ为目标的雷达散射截面积;Prmin为接收机的最小输入功率。
根据文献[9]可知:
(2)
式中:PD为目标发现概率;hB=KRL2,KR为表征雷达特性的系数;L为雷达探测边界的水平距离;h为无人机飞行高度;R为无人机与雷达的水平距离。
综上所述,雷达探测模型计算式为
(3)
1.2 火力威胁建模
高炮配有全方位旋转炮塔,炮弹弹道以一定初速形成的包络面所笼罩的空间就是高炮对空打击范围[10]。如图2所示。
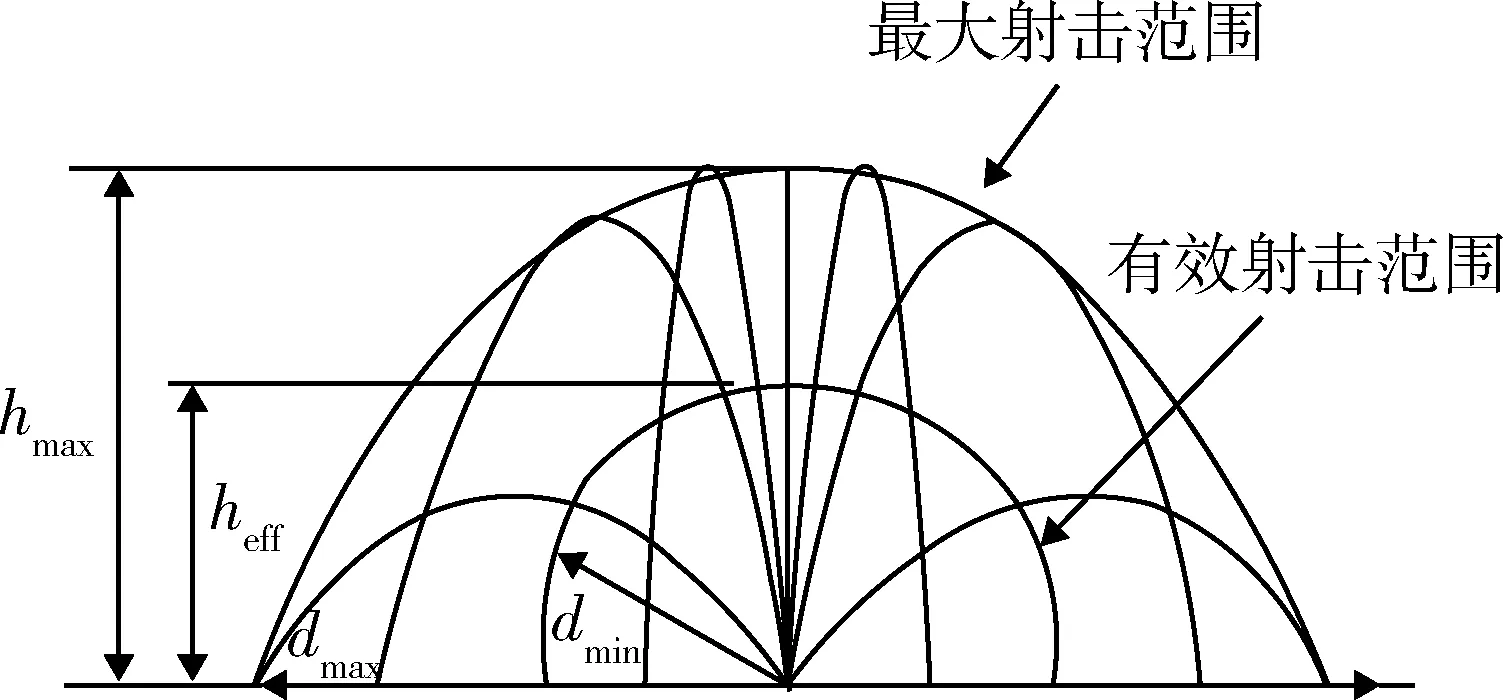
图2 火力威胁范围Fig.2 Fire threat range
图2中,hmax为最大射高,heff为有效射高,dmax为最大射程,dmin为有效斜距。无人机与高炮的相对距离在有效斜距以内,则炮弹能有效毁伤目标。同时,由于高炮其本身在射程顶点附近对高机动飞行目标的杀伤力急剧下降,所以,高炮有效射击范围近似为一个半球形区域。
高炮对目标的杀伤概率为
(4)
简化后的计算模型如下:
(5)
式中:PAK为高炮杀伤概率;PL为发射可靠概率;PR为炮瞄雷达正常工作概率;R为炮弹杀伤半径;σ为射击偏差;M为射击次数;N为一次发射的炮弹;d为无人机与高炮之间的距离。
1.3 导弹威胁建模
导弹的杀伤范围即杀伤区,其由目标特性、武器的物理特性和射击条件所决定。典型的低空导弹杀伤区范围近似为腰鼓型,剖面呈明显的规律性,左右对称[11]。如图3所示。

图3 导弹威胁范围Fig.3 Missile threat range
图3中,AB是导弹杀伤区高界,它对应的参数是杀伤目标的最大高度Hmax。BC是导弹杀伤区远界,它对应的参数是杀伤区远界的斜距Dr。AED是杀伤区近界,它对应的参数是杀伤区近界的斜距Df和最大高低角εmax。DC是杀伤区的低界,它对应的参数是杀伤目标的最低高度Hmin,h为杀伤区的纵深。
低空导弹杀伤概率为
PM=DRC[1-(1-AYW)N],
(6)
式中:D为地空导弹的雷达探测概率;R为低空导弹雷达截击引导概率;C为信息传输转换概率;A为导弹可靠发射概率;Y为导弹飞行可靠概率;W为导弹单发杀伤概率;N为导弹一次发射数量。
但是,在实际应用时往往根据在低空导弹杀伤区内,无人机与导弹距离越小,被击落的概率越大的原则,简化计算模型。同时无人机所受的威胁程度与相对水平距离符合相关的泊松分布,则
(7)
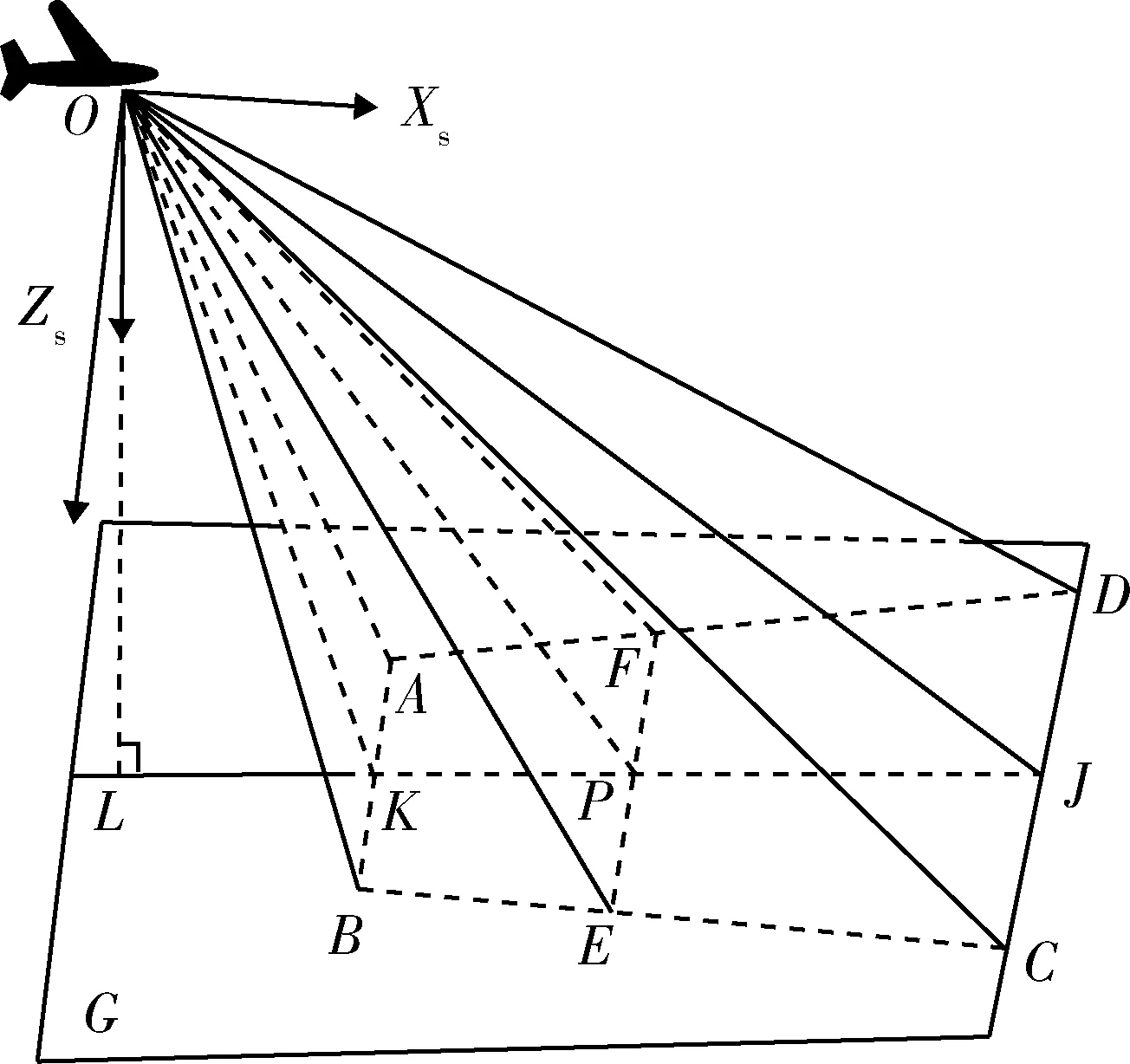
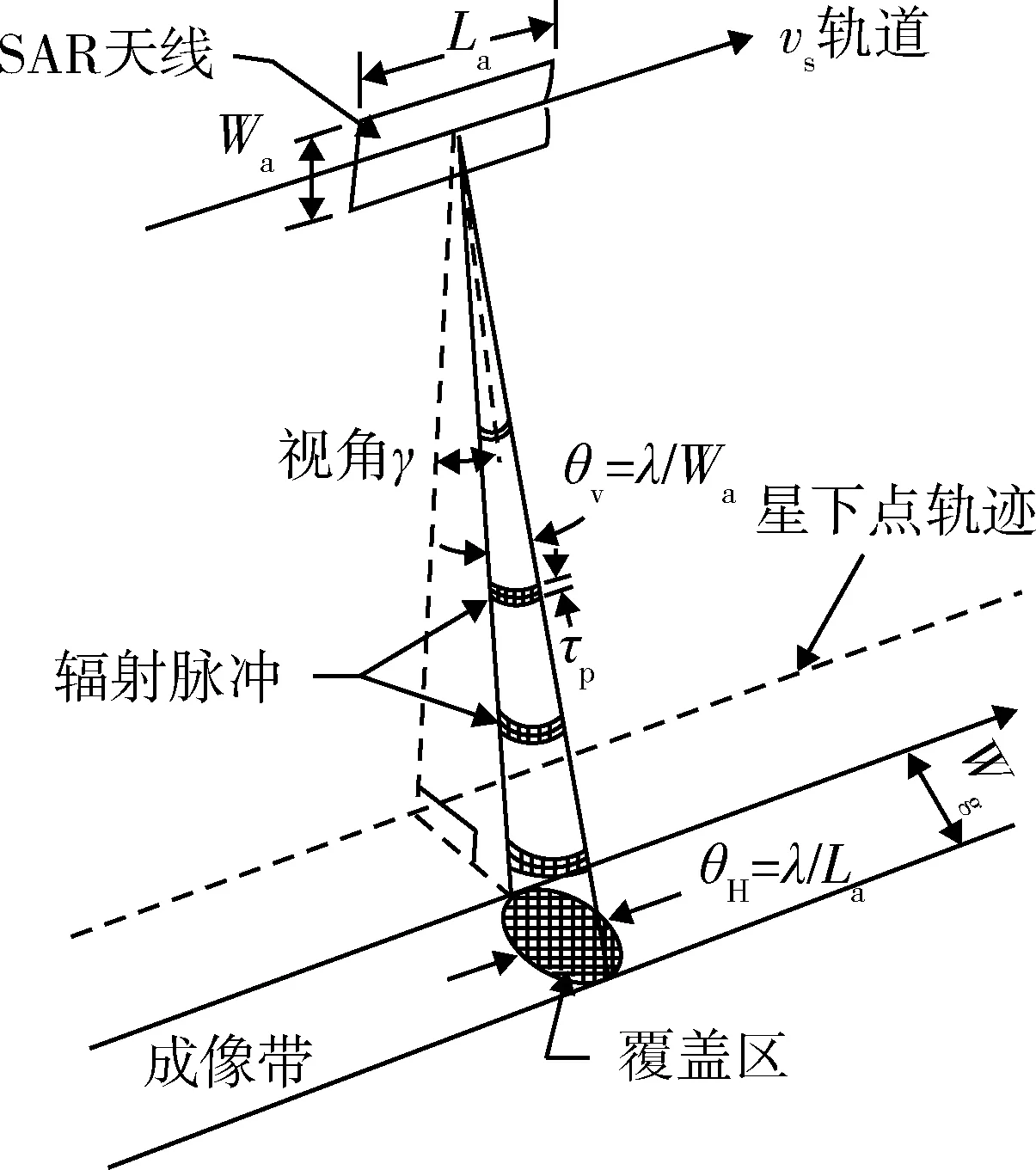
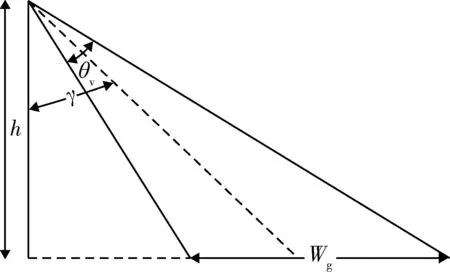
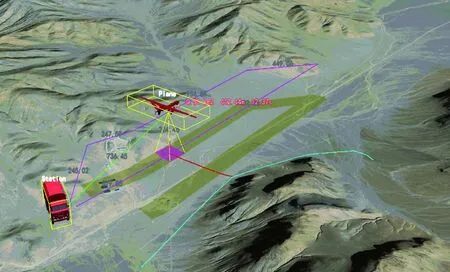
此时,认为d 无人机与测控站之间完全依赖无线链路进行信息的交互和控制。但在飞行过程中易受到地形地物的影响,产生链路盲区,使得地面人员无法实时有效掌握飞行动态,飞行安全的不确定性因素增加。所以在规划航迹时,有必要结合链路通视模型,使得任务航迹尽可能减少链路盲区。 无人机与测控站的链路通视模型符合点到点的通视模型。即对任意给定的空间地形上的2点M和N,M为视点,N为目标点,当N点高度大于盲区高度时,MN点能相互通视;反之,则MN点不能通视[12]。 链路通视算法步骤如下: 假设V点是与无人机通信的测控站位置,坐标为(xv,yv,zv),P点是无人机的位置,坐标为(xp,yp,zp)。VP两点连线的俯视图如图4所示。 图4 链路通视俯视图Fig.4 Top view of link communication (1) 在V′P′之间,按照一定等分原则(精度要求越高,等分距离越小),选取中间节点Pi,可求得Pi点的水平坐标(xi,yi),然后通过反距离加权插值法[13]求得Pi点的高程zi。 (2) 计算V到Pi各点以及P点的仰角斜率。 Ki=(zi-zv)/Lvpi,i=1,2,…,n, (8) 式中:Lvpi为V到Pi各点的水平距离;Lvp为V到P点的水平距离。 (3) 取各点仰角斜率Ki的最大值,即Kmax=maxKi,如果Kvp>Kmax,则VP可相互通视,盲区间隙高度为H=0,否则P被VP之间的地形地物遮蔽,不能相互通视,盲区间隙高度为 H=KmaxLvp+zv-zp. (9) 对于制定无人机侦察机的任务方案时,最重要是要确保获得的侦察数据能够满足后端情报处理的要求。所以从情报处理的角度规划任务时,可以依据各类载荷对地成像模型,结合任务要求,制定飞行高度等航迹参数。 图5是典型的可见光对地成像模型[9],红外成像与可见光类似,不再区分讨论。 图5 可见光对地成像Fig.5 Visible light imaging to earth 当无人机以一定高度h保持平飞,且俯仰角α和滚转角β均为0,偏航角为ψ。如图5所示,OP表示探测轴中心,∠LOP即为载荷的俯仰角φ,G表示地面,四边形ABCD就是载荷对地成像的瞬时范围。∠KOJ=2αp,∠EOF=2αv分别为载荷的纵向视场和横向视场,对应的成像距离为dv=KJ和dl=(AB+CD)/2。 根据几何关系可知: S=dv·dl, (10) 当φ=0时,即对地垂直侦察模式。 SAR雷达对地成像时,选择的工作模式不同,成像形式也不相同。但SAR雷达对地成像的分辨率是固定的(每种工作模式下,都对应几种固定的分辨率),与飞行高度无关,只与自身性能有关。图6为SAR雷达对地成像的一种工作模式[14]。 图6 SAR对地成像Fig.6 SAR Imaging to earth 图7中,h为飞行高度,γ为视角,θv为俯仰波束宽度,λ为波长,Wa为天线方位向长度,Wg为成像带宽度。 在讨论SAR雷达3种不同工作模式下的侦察模型前,首先对成像带的宽度Wg进行讨论和计算。 图7 Wg的计算Fig.7 Wg calculation 在飞行高度较高的情况下,由于θv较小,可以用弧长近似代替成像带的宽度Wg。根据弧长公式和三角关系可以得到SAR雷达的成像带宽度: (11) (1) 条带模式 条带模式对于地面的一个条带进行成像,条带的长度仅取决于雷达移动的距离,方位向的分辨率由天线的长度决定。由于其视角γ不变,所以成像带宽度Wg不会发生改变,当机载SAR以速度v匀速直线飞行时,其单位时间内的侦察面积计算公式为 (12) (2) 扫描模式 扫描模式相较于条带模式,主要区别在于牺牲了分辨率去增加侦察的范围,等价于增大了其在俯仰方向的波束宽度,从而增大了成像带宽度。在扫描模式下可以将扫描条带数引入其侦察模型之中,其单位时间内的侦察面积计算公式为 (13) (3) 聚束模式 聚束模式下,波束指向的控制可以在短时间内模拟出一个较宽的天线波束,但是波束指向不可能永远向后,最终还是要调回前向,这就意味着地面覆盖区域是不连续的,即一次只能对地面的一个有限圆域进行成像,最佳的侦察域是以成像带宽度Wg为直径的圆,其侦察面积计算公式为 (14) 任务规划制定的飞行航迹必须是可飞的,不仅仅要满足链路要求、成像要求以及飞行安全的要求,也要满足无人机自身的运动学限制,如无人机的飞行航迹应处于最大转弯曲率之内等[15]。常见的无人机性能约束主要包括以下几点: (1) 最大航程 最大航程限制了规划航迹的总长度必须小于或等于预先设定的最远距离。主要取决于携带的燃油量以及飞行的时间和速度。该约束可表示为 (15) (2) 最大/最小飞行高度 最大/最小飞行高度限制了无人机在飞行航迹上的高度范围。最大飞行高度一般小于实用升限,以确保无人机能够达到这一高度。最小飞行高度又称安全高度,即无人机离地飞行的最低高度,尤其是无人机做地形跟随飞行时,避免无人机与地面碰撞。该约束可表示为 Hmin≤H≤Hmax, (16) 式中:Hmin为最小飞行高度;Hmax为最大飞行高度。 (3) 最大/最小飞行速度 无人机的飞行速度取决自身的动力系统,也与战场环境、任务相关。如低空突防时,允许速度在一定范围内变化;在巡航侦察时,一般定速。该约束可表示为 vmin≤v≤vmax, (17) 式中:vmin为最小飞行速度;vmax为最大飞行速度。 (4) 最大爬升/下滑角 最大爬升/下滑角限制了无人机在规划的航迹上爬升或者下滑的角度范围(等效于高度范围)。该约束可表示为 (18) 式中:zi和zi+1为第i段航路的起点和终点的高度;li为第i段航路水平投影的长度。 (5) 最小转弯半径 最小转弯半径是指无人机在水平面以极限过载作圆周运动时的圆周半径。该约束可表示为 (19) 式中:v为速度;g为重力加速度;φmax为无人机最大滚转角。 在进行航迹规划时,也可以将无人机圆周运动的航迹离散为一系列的航迹段,这样就将最小转弯半径的约束转化为最小转弯步长Lmin和最大转弯角θmax的约束。如图8所示。 由几何关系可知: (20) 式(20)即为最小转弯半径Rmin与最小转弯步长Lmin、最大转弯角θmax三者之间转换关系式。 (1) 实验平台 实验室自研的无人机任务规划系统。 (2) 实验内容及相关参数设置 在某区域地理信息环境下,将任务规划约束空间模型和航迹规划算法结合,规划生成满足任务要求的可行航迹。 算法仿真参数如表1所示。 表1 仿真参数设置Table 1 Simulation parameter settings 将约束空间模型结合航迹规划算法,得到的仿真结果如图9所示。 图9 航迹规划实验Fig.9 Simulation results of path planning 将实验结果分析如下: (1) 红色线条表示任务航迹;绿色线条表示无人机与测控站的通视情况(绿色表示通视正常,红色表示非通视情况);无人机下方四边形区域表示载荷瞬时成像范围;黄色条带区域表示无人机沿任务航迹侦察所覆盖的区域。 (2) 无人机航迹规划算法结合链路通视模型,可优先搜索满足链路通视条件的航迹,确保无人机飞行状态可实时监控,保证飞行安全。 (3) 利用载荷成像模型可评估航迹成像覆盖范围,以此评估航迹的侦察效能,确保规划航迹符合任务要求。 (4) 以无人机性能模型为航迹规划的约束条件,来搜索可行航迹时,可有效约束航迹的可飞性,使得无人机沿着既定航迹飞行。 本文根据无人机任务规划的实战化要求,建立和完善了其约束空间的各类约束模型,并系统性分析了各类模型与任务规划之间的耦合关系。 (1) 战场威胁模型分别建立了3类典型陆战场武器系统的作用范围及毁伤概率模型。可依据威胁模型,规划相应的避让航迹,保证无人机不被敌方武器系统发现或者击落。 (2) 链路通视模型是依据视距链路的特性,建立无人机与测控站之间通信链路的通视分析模型。在规划航迹时,可结合链路通视模型,尽量减少航迹中的链路盲区。 (3) 载荷成像模型建立了无人机常见的几种侦察载荷对地成像模型。结合具体任务目标识别和效能评估的要求,可计算相应的航迹参数和评估结果。 (4) 无人机性能模型主要是约束飞行航迹的可飞性。制定的飞行航迹必须是可飞的,也就是满足无人机自身的运动学限制。2 链路通视建模

Kvp=(zp-zv)/Lvp,3 载荷成像建模
3.1 可见光成像
3.2 机载SAR雷达成像
4 无人机性能建模
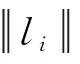
5 仿真实验
5.1 实验设置

5.2 实验结果及分析
6 结论

