一类右聚焦离散分数阶边值问题多个正解的存在性
郭彩霞,张慧芬,郭建敏
(山西大同大学 数学与统计学院,山西 大同 037009)
0 引言
近30年来,连续型分数阶微积分理论已广泛应用于数学、工程学、流体力学、经济学等各个领域,见文献[1-7]。最近离散的分数阶微积分理论也逐步引起学者们的关注,并取得一定的研究成果,见文献[8-16]。Goodrich在[8]和[9]中研究了两类带有局部条件的离散分数阶差分系统。文献[10-12]中Atici和Eloe给出一系列时标上的离散分数阶微分方程初边值问题的基本理论。在文献[13-16]中应用经典的不动点定理得到离散分数阶边值问题解的存在性。
本文将考虑以下非线性离散的分数阶边值问题,
(1)
其中1<ν≤2,t∈[0,b+1],f:[ν-1,ν+b]×R×R→R连续,b∈0.在文献[8]中作者利用锥拉伸锥压缩不动点定理得到(1)存在唯一解的充分条件,本文将运用Avery-Peterson不动点定理得到(1)存在三个正解的充分条件。虽然Avery-Peterson不动点定理是研究整数阶非线性边值问题多个正解存在性的经典工具,就作者所知,目前还没有应用Avery-Peterson不动点定理研究离散分数阶边值问题的文献。主要原因是对于分数阶微分方程来说,难于根据分数阶导数的符号来判别函数的凹凸性,所以限制了此定理在分数阶边值问题的应用。为了克服这一困难,本文通过定义一个特殊的锥,同时推导Green函数的新性质,得到未知函数的凹凸性。
1 预备知识
下面我们给出一些相关的定义和结论,有关证明见文献[10-12]中任何一篇。
定义1 对任意的t和ν,如果下式右端有意义,定义
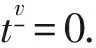
定义2 定义函数f的ν(ν>0)阶分数阶和为
其中t∈{a,a+1,…}=a.定义函数f的ν阶Caputo分数阶差分为
Δνf(t)=ΔNΔ-(N-ν)f(t),
其中t∈a+N-ν,N∈且满足0≤N-1<ν≤N.
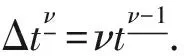
引理2 设μ,ν>0,f:a→,Δ-ν[Δ-μf(t)]=Δ-(ν+μ)f(t)=Δ-μ[Δ-νf(t)],其中t∈ν+μ+a.

定义3 设E为实Banach空间,定义非空凸闭集P为一个锥,满足(1)对于任意u∈P,a≥0,则au∈P.(2)若u,-u∈P,则u=0.
定义4 如果锥P上的连续映射β:P→[0,+∞),∀x,y∈P,0<λ<1,满足
β(λx+(1-λ)y)≤λβ(x)+(1-λ)β(y),
则称β为非负连续凸函数。
如果锥P上的连续映射α:P→[0,+∞),∀x,y∈P,0<λ<1,满足
α(λx+(1-λ)y)≥λα(x)+(1-λ)α(y),
则称α为非负连续凹函数。
设γ、θ为锥P上的非负连续凸函数,φ为锥P上的非负连续凹函数,ψ为锥P上的非负连续函数。对于正数a、b、c、d,定义如下凸集:
P(γ,d)={x∈P|γ(x) P(γ,φ,b,d)={x∈P|b≤φ(x),γ(x)≤d}, P(γ,θ,φ,b,c,d)={x∈P|b≤φ(x),θ(x)≤c,γ(x)≤d}, 定义闭集R(γ,ψ,a,d)={x∈P|a≤ψ(x),γ(x)≤d}. (S2)当x∈P(γ,φ,b,d),有φ(Tx)>b,θ(Tx)>c, (S3)当x∈R(γ,ψ,a,d),ψ(x)=a,则0∉R(γ,ψ,a,d),ψ(Tx) γ(x1) 引理5[8]分数阶边值问题(1)的解为 引理6[8]引理5中的Green函数满足以下性质: (1)G(t,s)≥0,∀(t,s)∈[ν-1,ν+b+1]×[0,b+1]; 证由引理5和6知 从而 注意到y为(1)的解,当且仅当y为算子T的不动点 其中G(t,s)是引理5中的Green函数,T|B→B, B={y|[ν-2,(ν+b+1)]→R|y(ν-2)=0=Δy(ν+b)} 定义锥K⊂B,且 引理9令算子T|K→K满足 则T|K→K是全连续的。 证K⊂B,先证T|K→K. 由于 同时当y∈K时,(Ty)(t)≥0,所以Ty∈K,易证得T是全连续。 令α是锥K上的非负连续凹函数,β,θ为锥K上的非负连续凸函数,φ,ψ为锥K上的非负连续函数,满足 由引理6和7知,以上函数满足 γθ(y)≤φ(y)≤θ(y)=ψ(y),‖y‖≤γ4β(y),y∈K,其中γ4=max{1,γ}. 定理1 假设(H1)-(H3)成立,则(1)至少有三个正解y1、y2、y3,且满足 从而∀y∈P(β,θ,φ,b,c,d),φ(Ty)>b. 最后证明引理4中的(S3)也成立。由于ψ(0)=0,且0∉R(β,ψ,a,d).假设x∈R(β,ψ,a,d)且ψ(x)=a,根据(H3)可得 这样引理4的条件全部满足,从而(1)至少有三个正解y1、y2、y3,满足 考虑分数阶边值问题 (2) 可检验(2)中非线性项满足定理1的全部条件,从而(2)至少有三个正解y1、y2、y3,满足
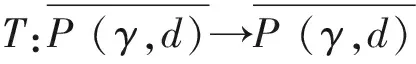


2 主要结果及证明
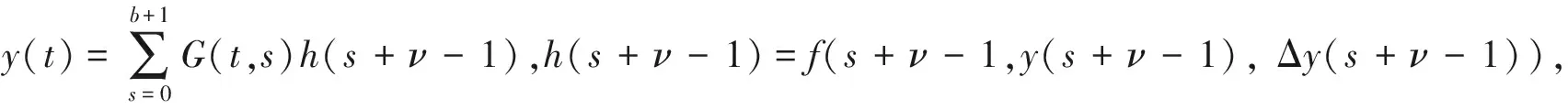

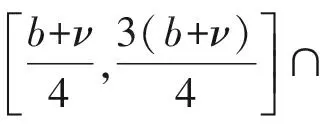

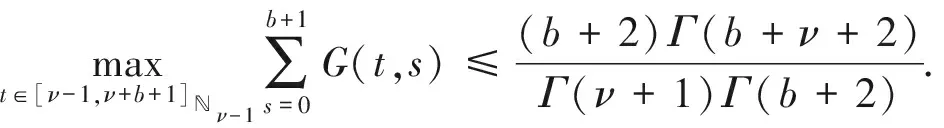


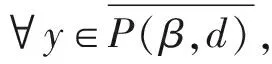
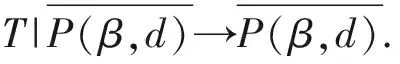
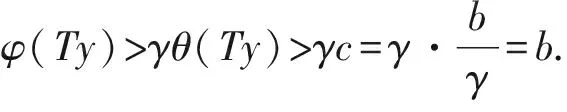
3 例子