高频变压器绕组布局对分布参数和功耗的影响
杨欢,张军朝*,张俊虎,张建,张毅
(1.太原理工大学 电气与动力工程学院,山西 太原 030024; 2.山西省电气传动及物联网工程技术研究中心,山西 太原 030024; 3.山西太原天地方圆电子科技有限公司,山西 太原 030024;4.太原市城市照明管理处,山西 太原 030024)
0 引言
随着科学技术的发展,开关电源凭借其体积小、重量轻以及可靠性高的优点,逐步取代了线性稳压电源并广泛应用于各行各业[1]。然而,随着工作频率的提高,开关电源内部分布参数的影响也越来越明显,功率损耗也在逐渐增加[2]。分布参数的存在不仅会引起谐振现象的发生,而且会在高频变压器电压、电流变化的瞬间在开关管上产生电流、电压尖峰,容易损坏开关管并且增加了功率损耗[3]。功率损耗不仅使得开关电源整体能量转换效率降低,也加速了其内部元器件的老化,对开关电源的可靠性及使用寿命产生了非常不利的影响。因此,如何降低高频变压器的分布参数成为目前众多专家、学者研究的热点。
高频变压器的分布参数主要有漏感和分布电容,它们主要受绕组布局情况(如绕组绕制结构、连接方式以及绝缘层厚度)的影响,文献[4]分析了分布参数对高频变压器效率的影响,并提出了采用交叉绕制的方式减小漏感,提高能量转换效率的思路。文献[5]研究了无交叉换位、部分交叉换位以及完全交叉换位三种绕制结构对漏感的影响,提出了通过提高绕组交叉换位程度以及降低绕组层数的办法来降低漏感。文献[6]着重分析了不同绕制结构对分布电容的影响,并提出了分布电容的软件提取方法。然而,上述三篇文献仅仅分析了不同绕组结构对于漏感或者分布电容的影响,并未同时考虑不同绕制结构对于这两种分布参数的影响,不利于指导绕组的设计。
本文针对高频变压器绕组不同绕制结构、连接方式以及绝缘层厚度对漏感和分布电容两种参数的影响分别进行了理论分析、仿真实验、实际设计及测试,得到了分布参数及功率损耗均较低的绕制结构及绝缘层厚度范围值,为设计低功耗的高频变压器提供了理论及实际参考。
1 分布参数产生的机理及影响
1.1 漏感产生的机理及影响
为方便分析漏感和分布电容的产生机理,给出如图1所示的高频变压器等效电路图。高频变压器在运行过程当中,初级侧与次级侧的磁通没有全部经过磁芯耦合,有一部分磁通经空气构成闭合回路,这部分磁通称为“漏磁通”,产生的电感称为“漏感”,对应于图1中的L10、L20。漏感的存在不仅使得开关管在开通或关断时,漏感储能释放,会在开关管上产生电压尖峰[7-8],增大开关管的开关损耗、容易损坏开关管并且增大漏极钳位电路的损耗。除此之外,漏感还可能与分布电容或电路中其他电容元件发生谐振,产生电磁干扰。同时,由于漏感在电路中是以串联的形式等效,在电压一定的情况下,电流有效值降低,输出功率降低,高频变压器能量转换效率降低。因此,降低漏感对于优化开关电源性能、保护开关管以及降低功率损耗是非常重要的。
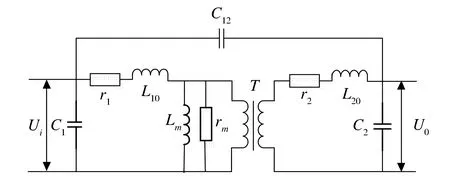
Fig.1 Equivalent circuit of high-frequency transformer图1 高频变压器等效电路
1.2 分布电容产生的机理及影响
开关电源初级侧绕组匝间、层间,次级侧绕组匝间、层间以及初级侧绕组和次级侧绕组之间,均存在分布电容,如图1中C1、C2和C12所示。一般来说,每层绕组匝间电容串联后的值远远小于层间电容值[9]。因此,重点考虑初级侧绕组或次级侧绕组层间电容以及初级侧绕组与次级侧绕组之间的电容对开关电源产生的影响。分布电容的存在不仅会在开关管开通或关断时产生电流尖峰,容易损坏开关管,而且分布电容可能与漏感发生谐振、产生电磁干扰、并对开关电源的性能及效率产生不利的影响。因此,降低分布电容对保护开关管、提高能量转换效率以及提高开关电源的性能至关重要。
2 分布参数的理论分析
2.1 漏感的理论分析
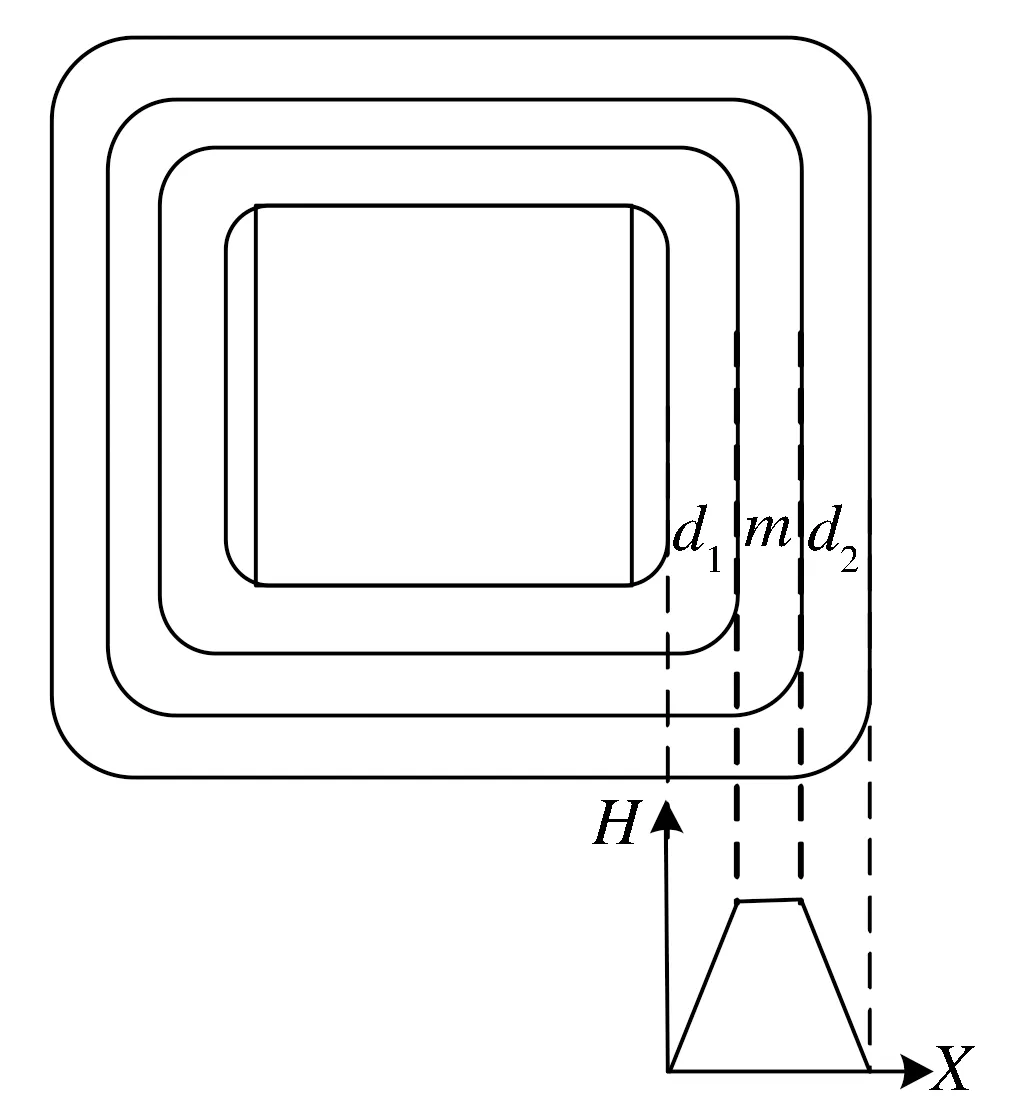
Fig.2 Section and magnetic field intensity distribution of single-layer coaxial winding图2 单层同轴式绕组截面及磁场强度分布
高频变压器的漏磁能量存储于漏磁场中,初级侧绕组、次级侧绕组磁动势相等,两绕组内电流流向相反。同轴式绕组可以视为长螺线管,各层绕组之间的磁场分布可等效为匝数相同的螺线管中的磁场。单层同轴式绕组截面及磁场强度分布如图2所示。
为方便对漏感及分布电容的分析,统一规定初级侧绕组单层厚度为d1,次级侧绕组单层厚度为d2,初级侧绕组和次级侧绕组之间的绝缘层厚度为m,初级侧绕组、次级侧绕组高度为h,初级侧绕组、次级侧绕组间的空间范围平均周长为A。由图2可以看出,初级侧绕组磁场强度H1沿绕组厚度方向逐渐增大,到达绝缘层部位达到最大,绝缘层范围内的磁场强度Hm保持不变,次级侧绕组磁场强度H2随绕组厚度的增加而减小,最终在次级侧绕组厚度为d2处降低为0。规定沿绕组厚度方向由里向外为x方向,则初级侧绕组沿厚度方向的磁场强度H1为:
(1)
绝缘层范围内的磁场强度Hm为:
(2)
次级侧绕组沿厚度方向的磁场强度H2为:
(3)
磁场能量密度ωm的定义为:
(4)
漏磁场能量Wm为:
(5)
整理结果为:
(6)
由于,漏磁场能量Wm与归算至初级侧的漏感Ls1的关系为:
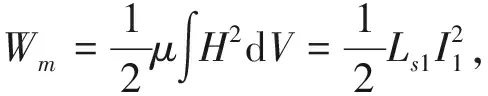
(7)
因此,归算至初级侧的漏感Ls1可由式(7)推导得到:
(8)
由此可见,归算至初级侧的漏感Ls1与绕组高度h成反比,与绝缘层厚度m成正比。因此,增加绕组高度,减小绝缘层厚度有利于增加绕组的耦合程度,降低漏感。由于初级侧绕组和次级侧绕组的磁势满足:N1I1=N2I2。代入公式(6)并利用漏磁场能量与归算至次级侧的漏感Ls2和次级侧电流I2的关系,可得到归算至次级侧的漏感Ls2。Ls2与Ls1的推导过程和结论完全一致。
高频变压器初级侧绕组和次级侧绕组之间的绕制结构可以分为简易绕制结构、三明治绕制结构以及交叉绕制结构三种。此三种结构的绕组排布及磁场分布分别如图3、图4和图5所示。简易绕制结构将初级侧绕组和次级侧绕组分别绕制。三明治绕制结构将初级侧绕组分成两部分,按照初级-次级-初级的顺序绕制。交叉绕制结构将初级侧绕组和次级侧绕组均匀交叉绕制。可以看出,从简易绕制结构到三明治绕制结构再到交叉绕制结构,磁场强度最大值在逐渐减小,整体漏磁场能量减少,绝缘层厚度减小,漏感也相应降低[10]。
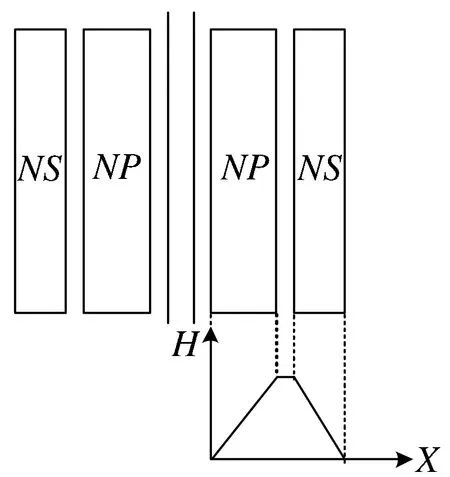
Fig.3 Winding′s layout and magnetic field distribution of simple winding structure图3 简易绕制结构的绕组布局及磁场分布
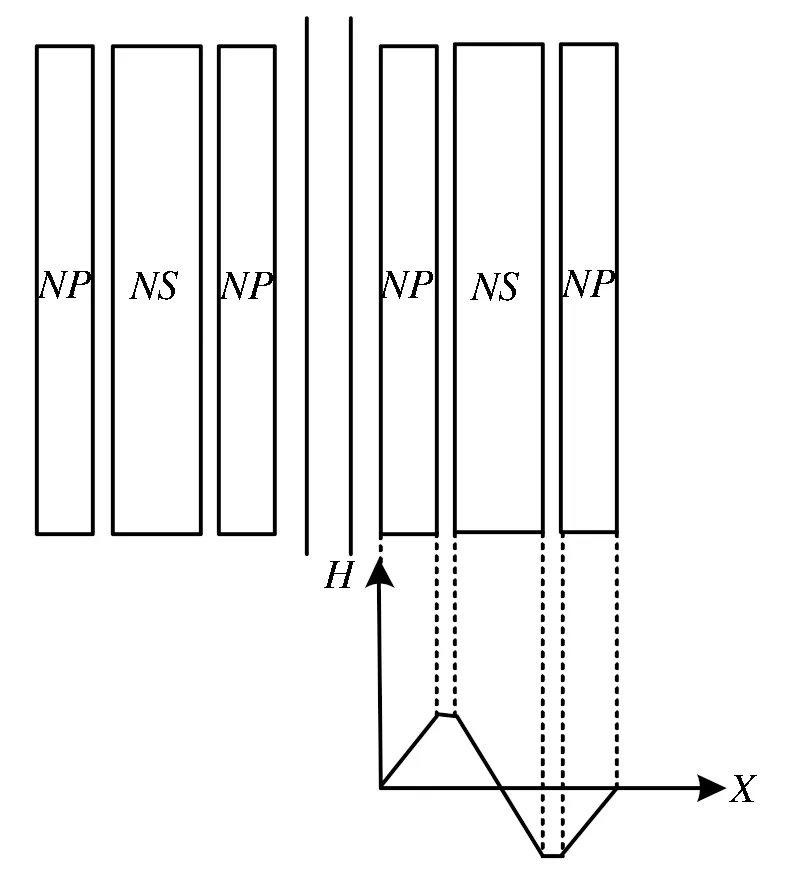
Fig.4 Winding′s layout and magnetic field distribution of sandwich winding structure图4 三明治绕制结构的绕组布局及磁场分布
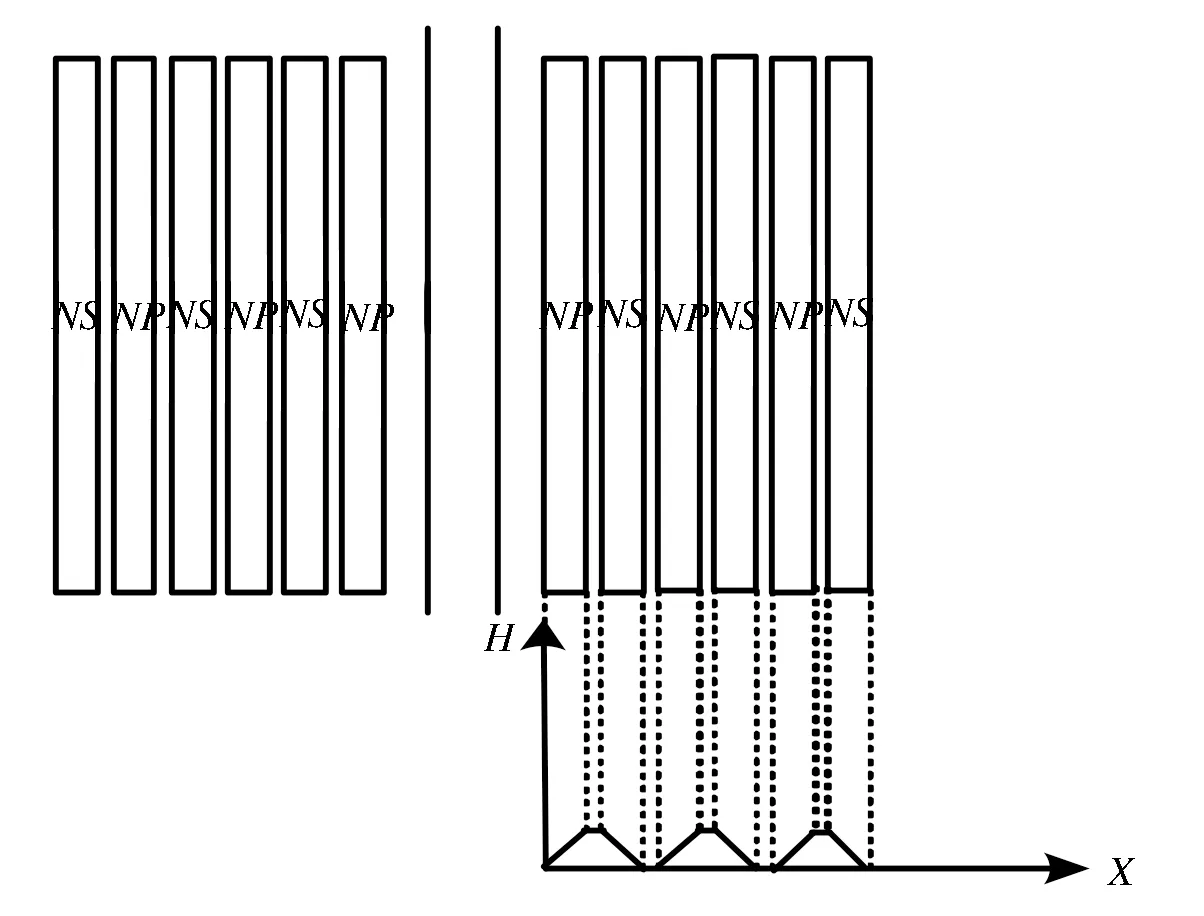
Fig.5 Winding′s layout and magnetic field distribution of cross winding structure图5 交叉绕制结构的绕组布局及磁场分布
2.2 分布电容的理论分析
1.初级侧绕组层间电容的理论分析
高频变压器分布电容的能量存储于电场中,可以依据电场能量与分布电容的关系推导得到初级侧绕组或次级侧绕组层间分布电容的表达式。初级侧绕组层间电容与次级侧绕组层间电容推导方式及结论完全一致,以初级侧绕组层间电容为例进行分析,按U型和Z型方式连接的绕组截面及电压分布如图6、图7所示。
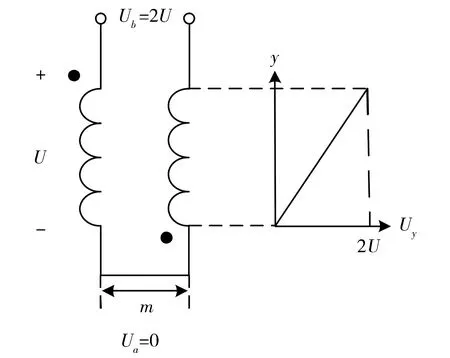
Fig.6 Winding′s section and voltage distribution of U-shaped connection图6 按U型方式连接的绕组截面及电压分布
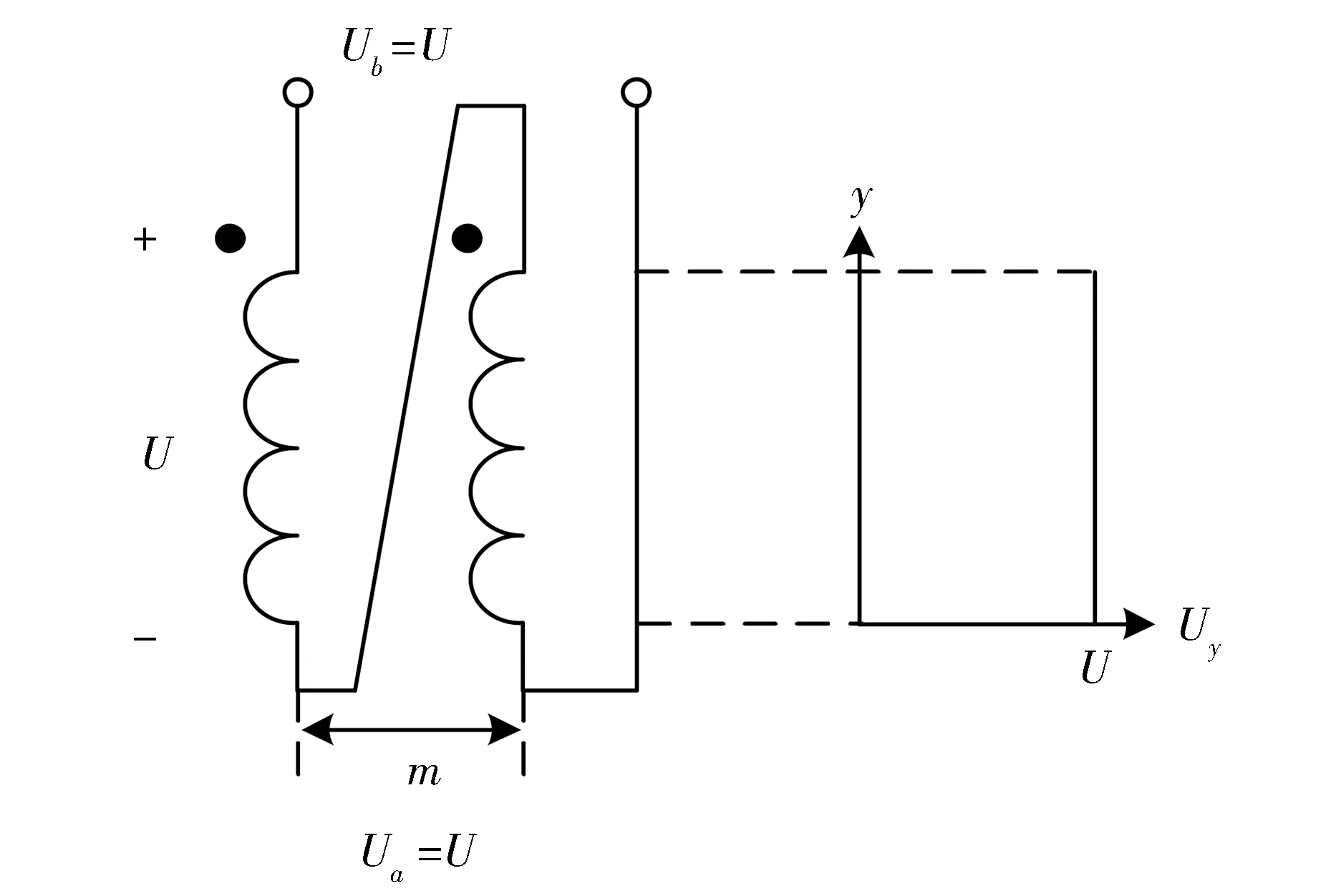
Fig.7 Winding′s section and voltage distribution of Z-shaped connection图7 按Z型方式连接的绕组截面及电压分布
规定沿绕组高度方向由底端向顶端为y方向,初级侧绕组底端电位差为Ua,顶端电位差为Ub。假设绕组均匀分布,则沿着绕组高度方向的电位线性变化。若每一层绕组两端压差为U,则图6中,Ua=0,Ub=2U,任意高度y的电位差Uy为:
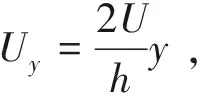
(9)
电场能量密度we的定义式为:
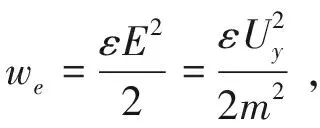
(10)
电场能量We为:
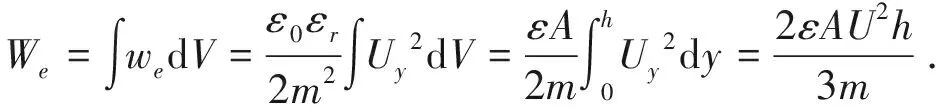
(11)
由于电场能量We与分布电容C1的关系为:

(12)
因此,初级侧绕组层间分布电容C1可由式(11)和式(12)推导得到:
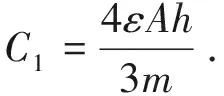
(13)
图7中,Ua=Ub=U,任意高度y的电位差Uy=U,则Z型方式连接的初级侧绕组层间分布电容C1为:
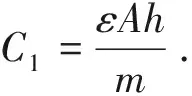
(14)
根据式(13)、式(14)可以看出,采用Z型连接方式的分布电容较U型连接方式的分布电容小,并且初级侧绕组层间电容与绕组高度成正比,与绝缘层厚度成反比。
3 初级侧绕组与次级侧绕组层间电容理论分析
初级侧绕组与次级侧绕组层间电容的分析不涉及绕组连接处绕制方式的问题,因此可以以平行板电容器为模型进行类比,分布电容C12为:
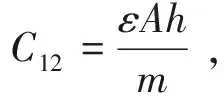
(15)
由式(15)可知,初级侧绕组与次级侧绕组间分布电容C12与绕组高度h成正比,与绝缘层厚度m成反比。
由此可知,绕组层间电容均正比于绕组高度,反比于绝缘层厚度。减小绕组高度,增大绝缘层厚度可以减小层间电容值。然而,此结论与降低漏感的措施恰恰相反[11]。绕组高度与磁芯型号规格有关,而磁芯型号规格的确定在高频变压器最开始设计的时候就由功率体积设计法经计算和选型得到,并且由于开关电源正在朝着小型化的方向发展[12],增大绕组高度对于减小开关电源体积不利,往往不会通过增加绕组高度的办法来降低漏感。因此,绝缘层厚度便成为影响漏感及分布电容的关键因素。
4 仿真结果及分析
4.1 仿真模型的建立
为得到绝缘层厚度与漏感及分布电容的关系,以便设置恰当的绝缘层厚度,使得漏感和分布电容都比较小,降低分布参数带来的电磁干扰,电压、电流尖峰以及功率损耗。由于Z型连接方式分布电容小。因此,在Ansoft Maxwell软件中分别建立简易绕制结构、三明治绕制结构以及交叉绕制结构且不同层绕组连接处以Z型方式连接的高频变压器模型。高频变压器模型参数见表1所示。为简化绕组模型,提高运算速度,建立1/2高频变压器模型。简易绕制结构的1/2高频变压器模型如图8所示,三明治绕制结构及交叉绕制结构的1/2高频变压器模型的绕组布局同图4和图5,此处仅以简易绕制结构示例。

表1 高频变压器模型参数表
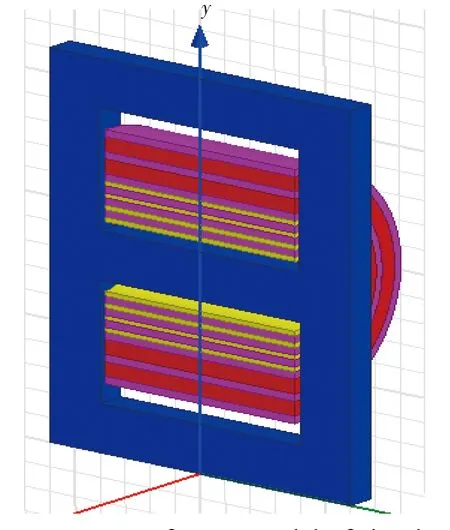
Fig.8 Two-dimensional plan of 1/2 high-frequency transformer model of simple winding structure图8 简易绕制结构1/2高频变压器模型二维平面图
4.2 仿真结果及分析
通过改变绝缘层厚度m,利用Ansoft Maxwell软件提取三种绕组结构在不同绝缘层厚度下的初级侧漏感值Ls1、初级侧分布电容C1、初级侧绕组和次级侧绕组之间的分布电容C12以及分布参数总损耗Ploss,得到如图9、图10、图11以及图12所示的仿真结果。

Fig.9 Relational curve between Ls1 and m图9 Ls1和m的关系曲线

Fig.10 Relational curve between C1 and m图10 C1和m的关系曲线

Fig.11 Relational curve between C12 and m图11 C12和m的关系曲线
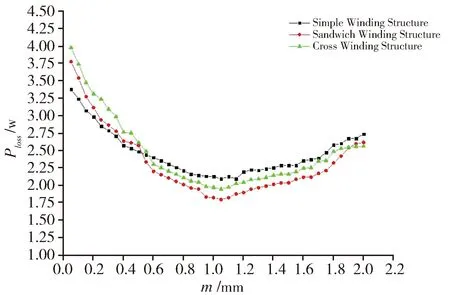
Fig.12 Relational curve between Ploss and m图12 Ploss和m的关系曲线
图9所示的仿真结果表明:三种绕制结构的初级侧漏感Ls1随绝缘层厚度m的增加均呈现上升的趋势。相同绝缘层厚度下,简易绕制结构的漏感值大于三明治绕制结构和交叉绕制结构的漏感值。图10所示的仿真结果表明:三种绕制结构的初级侧分布电容C1随绝缘层厚度m的增加均呈现下降的趋势。相同绝缘层厚度下,交叉绕制结构的分布电容值大于三明治绕制结构和简易绕制结构的分布电容值。图11所示的仿真结果表明:三种绕制结构的初级侧绕组和次级侧绕组之间的分布电容C12随绝缘层厚度m的增加均呈现下降的趋势。相同绝缘层厚度下,交叉绕制结构初级侧绕组和次级侧绕组之间的分布电容值大于三明治绕制结构和简易绕制结构初级侧绕组和次级侧绕组之间的分布电容值。图9、图10以及图11的曲线趋势均与理论分析得到的结论相一致。图12所示的仿真结果表明:分布参数总损耗Ploss随绝缘层厚度m的增加呈现先下降后上升的趋势。当绝缘层厚度在1.0 mm~1.2 mm范围内时,各种绕制结构的分布参数总功率损耗最低,并且三明治绕制结构高频变压器的功率损耗在绝缘层厚度为1.1 mm附近时达到最低。由于漏感和分布电容随绝缘层厚度变化的趋势恰好相反。因此,在绝缘层厚度偏薄和偏厚时,会分别造成分布电容和漏感偏大的情况,进而导致分布参数的功耗偏大。当绝缘层厚度在适当的范围内时,各种绕组结构的分布电容和漏感均达到大小适中的值,避开了漏感或分布电容最大的情况,分布参数的功耗低。而三明治绕制结构的绕组之间的耦合性介于简易绕制结构和交叉绕制结构之间,更易平衡两种分布参数,实现功耗最低。因此,图12所示的趋势正确。
5 实验验证

Fig.13 Proto of high-frequency transformer图13 高频变压器样机
基于上述仿真结果,设计了基于三明治绕制结构的不同层绕组连接处以Z型方式连接且绝缘层厚度为1.1 mm的高频变压器样机。高频变压器样机如图13所示。采用3259高频变压器测试仪对样机分布参数进行测量,测试结果见表2所示。将高频变压器样机及其他电子器件焊接至开关电源PCB样板制成开关电源样机。最后将开关电源样机与外围电路连接并进行测试,测试得到高频变压器效率达99.4%,开关电源整体效率达90.3%。测试结果表明:分布参数的测试结果与仿真结果基本一致,验证了仿真结果的正确性。并且设计的高频变压器效率满足超过95%~98%的常规设计要求[13],高频变压器及开关电源均具有较高的能量转换效率。

表2 样机实测数据
6 结论
本文首先从理论上分析了高频变压器中,简易绕制结构、三明治绕制结构和交叉绕制结构以及不同层绕组以U型和Z型方式连接对于漏感及分布电容的影响,接着在Ansoft Maxwell软件中建立不同绕制结构以Z型方式连接的高频变压器模型,对不同绝缘层厚度下的分布参数及功率损耗进行了仿真实验,仿真结果表明:以三明治结构绕制且在不同层绕组连接处以Z型方式连接的高频变压器功率损耗在绝缘层厚度为1.1 mm附近时达到最低。最后对设计的高频变压器进行了实验测试,测试得到的分布参数与仿真结果一致且高频变压器能量转换效率高。

