高中数学竞赛试题中圆锥曲线部分问题研究

☉安徽省临泉县第二中学 于 伟

数学是学生参加自主招生考试的重要科目，也是很多高校在自主招生复试中必考的科目之一.它不仅注重对学生数学基础知识的考查，还注重对学生数学思维和解题技巧等方面的考查.研究数学竞赛试题，对于拓宽学生的知识面，发展学生的数学思维具有重要的意义.在数学竞赛试题中，圆锥曲线部分的知识是一个重要的知识点，它也是高考数学中的重要知识点.该部分知识与解析几何相结合，为学生后续的数学学习打下基础，同时该部分知识包含了许多数学思想和数学模型，是学生将来研究数学问题的重要依据.

一、高中数学竞赛中圆锥曲线部分考题概述

通过对近几年数学竞赛试题的统计分析不难发现，圆锥曲线部分的知识占据着30分左右的分值，题型主要涉及选择题、填空题和解答题，其考查的知识点具有一定的综合性，涵盖了数列、不等式、平面向量和函数等.

二、高中数学竞赛试题中圆锥曲线部分例题分析

1.涉及圆锥曲线基本性质类的相关问题

圆锥曲线基本性质部分的问题是高中数学竞赛试题中经常出现的问题，该部分问题的难度较小，主要考查学生的基础知识和基本技能.在多数情况下，涉及圆锥曲线基本性质部分的考题多以选择题和填空题的形式出现，主要考查顶点、离心率、渐近线、焦点弦和切线等方面的知识.

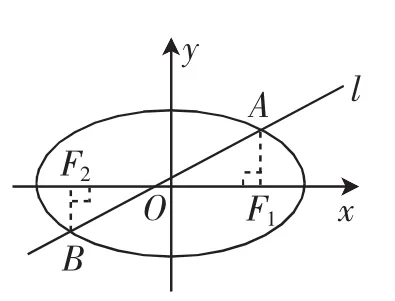
图1

例1如图1所示，一条斜率为的直线l与椭圆相交于A，B两点，其中A，B两点互异，且焦点在x轴上.A，B两点的投影分别与椭圆C的两个焦点F1和F2重合，那么椭圆C的离心率是多少？

问题分析：这道题的难度较低，在解决这一问题时，需要根据题意设出A点的坐标，然后代入椭圆=1中，再借助于离心率公式求出e.

解：设椭圆C的半焦距为c，根据题意可得点A的坐标为因为点A在椭圆C上，所以将其代入椭圆方程可得又因为，所以原式可变形为，解得，故

例2椭圆的短轴长等于多少？

问题分析：这一问题涉及圆锥曲线的极坐标方程部分的知识，该部分知识在高中数学竞赛大纲的要求范围内，但在高考数学考试范围以外，本题主要考查学生利用圆锥曲线的极坐标方程解决圆锥曲线问题的能力.在解决这一问题时，我们可以根据离心率e和焦点参数p的几何意义直接求出短半轴的长度.

解：因为e为离心率，p为极点到准线的距离），由

由b2+c2=a2，解得，即短轴的长度为

2.涉及轨迹类的相关问题

轨迹类问题是圆锥曲线部分的常考问题，在数学竞赛中，该部分知识也是常考点，其中主要考查学生利用定义法、转移法、参数法和交轨法等来求轨迹问题的能力.

图2

例3如图2所示，在△NPQ中，NP、NQ上的中线长之和为6，以PQ所在直线为x轴，以边PQ的中垂线所在直线为y轴建立平面直角坐标系，求顶点N的轨迹方程.

问题分析：在高中数学竞赛试题中，该题难度较低，学生可以利用定义法来完成此题的解答.

解：过N点分别作PE和FQ的平行线NM1和NM2交x轴于点M1和M2，其中E，F分别为NQ，NP上的中点，则.根据椭圆的定义可得，N点的运动轨迹为以和为左、右焦点的椭圆，则3，即该椭圆的方程为

3.涉及存在性的相关问题

在数学竞赛中，圆锥曲线部分有关存在性的问题是一个热门考点，该部分题型的难度较大，知识点之间的综合性和联系性较强，对学生的数学思想和知识应用的灵活性要求较高.一般情况下，这类问题主要涉及点是否存在、直线是否存在、参数是否存在和曲线是否存在等问题.

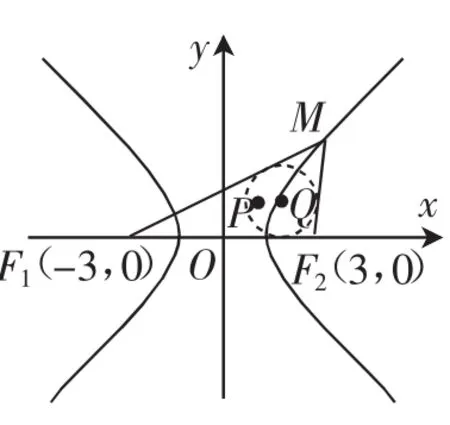
图3

问题分析：这是一道典型的求点是否存在的问题，是数学竞赛中的中档难度的问题.

解：根据题意可得F2（3，0）.假设存在点M（xm，ym），使得PQ∥F1F2.因为P为△F1F2M的重心，所以P点的坐标为为△F1F2M的内心，设△F1F2M的内切圆半径为r，则△F1F2M的面积为，则r=又因为，所以根据双曲线的性质可得|MF1|+|MF2|=4c，|MF1|-|MF2|=2a，则|MF2|=4，根据两点间的距离公式得=4.又因为点M在双曲线上运动，所以有，两式联合解得，所以存在点，使

例5已知抛物线E：y=mx2（m＞0），与直线l：x-y+2=0相交于M，N两点，G为MN的中点，过点G作GJ垂直于x轴，交抛物线于点J.问：是否存在实数m，使得？如果存在，求出m的值；如果不存在，请说明理由.

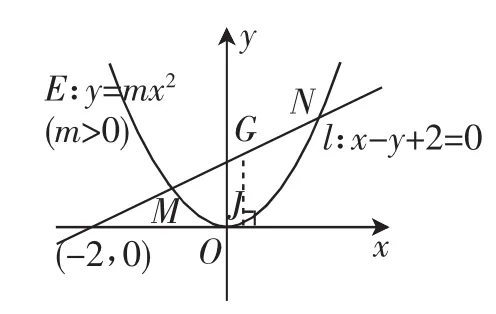
图4

问题分析：本题是一道关于实数根存在与否的问题，题目难度属于中档题型.通过题目中的已知条件我们可以知道|MN|=2|GJ|，又因为抛物线与直线相交于M，N两点，因此，可以联立方程组消去y，得到一个关于x的方程.根据根与系数的关系得出又因为M，N均在直线l上，则可求得G点的坐标为由此可求得J点的坐标为，最后根据两点间的距离公式和弦长公式求出|GJ|，|MN|的值，进而可得m的值.

解：假设存在实数m，使得，设M（xM，yM）、，因为，所以又因为G为MN的中点，所以|MN|=2|GJ|.因为M、N为抛物线E和直线l的交点，联立方程组整理可得mx2-x-2=0，根据根与系数的关系可得又因为G为MN的中点，所以，故G点的坐标为.根据题意可得，所以，根据两点间的距离公式可得，根据弦长公式可得，解得.所以存在实数，使得

三、小结

圆锥曲线是高中数学竞赛中的必考内容，该部分知识能够与其他部分知识相结合，考查学生对数学知识的应用能力及数学思想方法的掌握情况.将圆锥曲线部分知识加以梳理，能够有效地提高学生在数学竞赛考试中的解题速度，从而提高数学考试成绩.