一种用于矩形阵列的二维波达方向估计方法

王剑书，樊养余，杜 瑞，吕国云

(西北工业大学 电子信息学院，陕西西安，710129)

波达方向(Direction Of Arrival, DOA)估计是阵列信号处理领域的一个重要研究方向，并广泛应用于大量实际场景，比如雷达、声呐、麦克风阵列和通信系统等。通过传感器阵列接收单个或多个目标源的信号，形成阵列信号，而波达方向估计则是通过对阵列信号进行处理求得目标源方向的技术方法。早期的波达方向估计一般通过波束形成实现，这类方法实现简单，应用广泛，但对角度相邻的源的分辨能力欠佳。现代高分辨波达方向估计方法主要包括子空间类方法与稀疏重构方法。子空间类方法主要包括多重信号分类(MUltiple SIgnal Classification, MUSIC)[1]和旋转不变参数估计技术(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT)[2]等，稀疏重构方法主要包括l1范数最小化[3-5]和稀疏贝叶斯学习[6]等。

上述方法主要基于一维波达方向估计研究，尽管部分方法可以使用二维(Two-Dimensional, 2-D)阵列，对于二维波达方向估计(同时估计方位角和俯仰角)，大部分方法需要对空间角度进行网格化，对于角度的搜索也扩展到二维，这大大增加了计算负担。利用特殊结构的二维阵列，不少高效的二维波达方向估计方法被提出。对于均匀矩形阵列(Uniform Rectangular Array, URA)，文献[7]提出了基于酉ESPRIT的二维波达方向估计方法。对于均匀圆阵，文献[8-9]通过对其阵列流型进行贝塞尔函数重新表达，提出有效的类ESPRIT算法。对于L形阵列，文献[10-12]利用两个线阵的互相关矩阵，构造了有效的二维波达方向估计方法。文献[13-14]使用均匀矩形阵列或稀疏矩形阵列(Sparse Rectangular Array, SRA)，利用均匀矩形阵列协方差矩阵的二阶特普利茨结构，重构了其协方差矩阵，并通过二维ESPRIT方法进行波达方向估计。上述使用特殊二维阵列的波达方向估计方法无需对空间角度网格化，可以直接估计方位角和俯仰角。这种无网格的波达方向估计，称为无格波达方向估计。上述使用均匀矩形阵列或稀疏矩形阵列的方法有以下缺点：文献[7]的方法不能用于稀疏矩形阵列情形；文献[13]的快速无格最大似然方法(Fast Grid-less Maximum Likelihood, FGML)本质为加权的最小二乘法，由于未对协方差矩阵进行正定约束，在稀疏矩形阵列下估计性能一般；文献[14]使用的低秩矩阵重构(Low-Rank Matrix Reconstruction, LRMR)法，以核范数进行凸松弛，求解结果并不是最优。近年来发展起来无格一维波达方向估计方法(包括原子范数最小化(Atomic Norm Minimization, ANM)法[15-17]、加权原子范数法[18]和无格稀疏迭代协方差估计(Grid-Less SParse Iterative Covariance-base Estimation, GL-SPICE)方法[19-21]等)，表现出了非常良好的波达方向估计性能，尤其是文献[18]提出的使用log-det函数的稀疏测度，若将其应用于均匀矩形阵列或稀疏矩形阵列情形，可以进一步提高二维波达方向估计的性能。

笔者提出一种基于均匀矩形阵列或稀疏矩形阵列的二维无格波达方向估计方法。首先对协方差矩阵的二阶特普利茨结构进行更简洁的表达；然后根据文献[18]提出的稀疏测度，提出该二阶特普利茨矩阵的重构方法；最后通过二维ESPRIT方法[22]进行二维波达方向估计。笔者提出的方法需要多次求解半定规划(Semi-Definite Programming, SDP)问题，计算复杂度相对较高，但由于二阶特普利茨矩阵的重构结果比其他方法有更好的稀疏性，故能获得更好的波达方向估计结果。在仿真实验中，分别在均匀矩形阵列和稀疏矩形阵列下，对不同快拍数、信噪比(Signal-to-Noise Ratio, SNR)和相邻源角度间隔的均方根误差(Root-Mean-Square Error, RMSE)结果进行分析，验证了笔者提出的方法具有良好的波达方向估计性能。

1 均匀矩形阵列和稀疏矩形阵列的接收信号模型

使用均匀矩形阵列或稀疏矩形阵列，假设各阵元各向同性。为方便描述，先考虑均匀矩形阵列。如图1所示，将均匀矩形阵列置于xOy平面，x轴和y轴上阵元数目分别为Mx和My，记M0=MxMy；该阵列接收K个独立窄带源信号，最小阵元间距设为窄带信号中心频率的半波长λ/2，第k个入射信号的方位角和俯仰角分别为θk∈[-π,π]和φk∈[0,π/2]；令m=(mx-1)My+my，其中mx=1,2,…,Mx，my=1,2,…,My，则第m个阵元的坐标为((mx-1)λ/2,(my-1)λ/2)。该阵列信号快拍数据模型可以表示为

x=As+v，

(1)

其中，x(l)为阵列接收信号的第l个采样，称为第l个快拍，l=1,2,…,L，L为快拍数；x=[x(1),x(2), … ,x(L)]、s=[s(1),s(2), …,s(L)]和v=[v(1),v(2), …,v(L)]分别为观测信号、源信号和噪声的快拍构成的矩阵；A=[a(θ1,φ1),a(θ2,φ2), …,a(θK,φK)]，a(θk,φk)=ax(αk)⊗ay(βk)为第k个源信号方向的导向矢量，k=1,2,…,K，⊗为克罗内克积，ax(αk)=[1,exp(jπαk), …, exp(jπ(Nx-1)αk)]T，ay(βk)=[1, exp(jπβk), …, exp(jπ(Ny-1)βk)]T，j为虚数单位，(·)T为转置运算，且有

αk=cosθksinφk,

(2a)

βk=sinθksinφk。

(2b)

假设各阵元的噪声为独立同分布的高斯白噪声，其功率为σ2。若使用均匀矩形阵列的部分M(M>K)个阵元构造的稀疏矩形阵列，则阵列信号可以表示为

xΩ=ΓΩx=ΓΩAs+vΩ,

(3)

其中，ΓΩ∈{0,1}M×M0为选择矩阵，xΩ和vΩ分别为稀疏矩形阵列接收信号矩阵和噪声矩阵。均匀矩形阵列可以视为稀疏矩形阵列的特殊情形，此时对应的ΓΩ为M0维单位矩阵。图2给出了一个稀疏矩形阵列的示例，此时Mx=6，My=5，M=10，M0=30，根据此稀疏矩形阵列与均匀矩形阵列阵元位置的关系可知，ΓΩ由M0维单位矩阵IM0的第1、2、5、6、8、15、19、21、27和30行构成。

图1 均匀矩形阵列的信号模型

图2 稀疏矩形阵列与对应的均匀矩形阵列关系图

2 基于均匀矩形阵列或稀疏矩形阵列的二维无格波达方向估计方法

2.1 二阶特普利茨矩阵表达

对于模型式(3)，协方差矩阵为

(4)

(5)

(6)

2.2 二阶特普利茨矩阵重构

(7)

根据舒尔补理论[23]，优化问题式(7)等价为

(8)

(9)

(10)

优化问题式(10)的目标函数是非凸的，但可以使用优化最小化(Majorization-Minimization, MM)算法[24]，将其分为Q次半定规划问题求解，其中第q次求解的优化问题为

(11)

(12)

2.3 二维波达方向估计

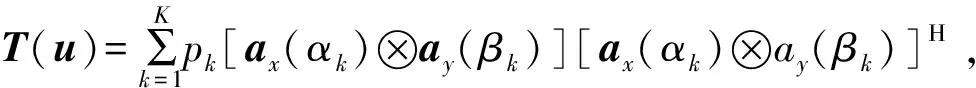
An-Ψn=An-,

(13)

(14)

(15a)

(15b)

2.4 对比分析

将笔者提出方法的计算复杂度与估计性能进行对比分析。对比的方法为最近提出的FGML[13]、LRMR[14]、ANM[17]和GL-SPICE[19]4种二维无格波达方向估计方法。

先考虑算法的计算复杂度，由复数乘法次数的阶数进行表达。二维ESPRIT方法可以使用截断的奇异值分解，计算复杂度为O(K2M0)[22]，5种方法均使用该方法进行二维波达方向估计。快速无格最大似然方法有闭式解，计算复杂度为O{(2Mx-1)3(2My-1)3}，在5种方法中最低；其他3种方法需要迭代求解，低秩矩阵重构的计算复杂度为O{(2MxMy-2Mx-2My+1)3T}，原子范数最小化与GL-SPICE的计算复杂度为O{(K2+2MxMy-2Mx-2My+1)3T},笔者提出方法的计算复杂度为O{(K2+2MxMy-2Mx-2My+1)3TQ}，其中T为各优化问题的迭代次数，并假设其在各方法中相等。可以看出，笔者提出的方法由于需要求解半定规划问题Q次，在5种方法中具有最高的计算复杂度。

再考虑波达方向估计性能。原子范数最小化实际上是l1范数最小化的连续域实现[17]；GL-SPICE是协方差矩阵的拟合方法[21]；低秩矩阵重构是利用无噪声条件下协方差矩阵低秩信息构造的方法[14]；快速无格最大似然方法并未约束协方差矩阵的正定性[13]；笔者提出的方法使用的稀疏测度是由原子l0范数通过log-det函数平滑替代而来的，在参数τ趋近于0时，其趋近原子l0范数[18]。因此，相比其他方法，笔者提出的方法能够提供更稀疏的解，从而可以获得更好的波达方向估计性能。节3的仿真实验可以验证该结论。

3 仿真实验

源信号使用零均值且方差为1的独立同分布的复高斯信号，每个阵元添加等功率的复高斯白噪声。接收信号信噪比定义为rSNR=10 lg(K/σ2)。使用均方根误差作为算法性能评价标准，方位角与俯仰角的总均方根误差可表示为

(16)

3.1 均匀矩形阵列情形

使用4×4的16元均匀矩形阵列。除了笔者提出的方法，同时仿真了二维ESPRIT方法(记为2-D ESPRIT)、快速无格最大似然方法、低秩矩阵重构、原子范数最小化、GL-SPICE和对应的克拉美罗界(Cramér-Rao Bound, CRB)[8]进行对比。

(1)快拍数的影响。设置源数目为2，真实方位角分别为-40.17°和80.23°，真实俯仰角分别为50.30°和60.25°。设置信噪比为3 dB，对不同的快拍数进行独立实验，结果如图3(a)所示。可以看出，2-D ESPRIT、原子范数最小化、GL-SPICE与笔者提出的方法在所有快拍数条件下的均方根误差均接近克拉美罗界，而快速无格最大似然方法与低秩矩阵重构只在快拍数不小于70时接近克拉美罗界，在低快拍数时均方根误差结果一般。

(2)信噪比的影响。同上设置两个源信号，设置快拍数为200，对不同信噪比进行独立实验，结果如图3(b)所示。可以看出，6种方法在-9 dB到12 dB的信噪比条件下的均方根误差均接近克拉美罗界，性能比较接近。

图3 均匀矩形阵列下的均方根误差仿真实验结果

(3)相邻源的影响。设置源数目为2，两个源的俯仰角均为50°，第1个源的方位角为-1°到1°随机产生，第2个源的方位角为第1个源的方位角加一个角度间隔，这里实验设置该角度间隔分别为2°，4°，…，16°，图3(c)显示了快拍数为200，信噪比为6 dB时的仿真实验结果。可以看出，原子范数最小化表现较差，其他方法的表现差别不大。

3.2 稀疏矩形阵列情形

使用图2所示10元稀疏矩形阵列。由于2-D ESPRIT无法直接使用，该情形下仿真快速无格最大似然方法、低秩矩阵重构、原子范数最小化、GL-SPICE、克拉美罗界与文中所述方法进行对比。

(1)考虑快拍数的影响。设置源数目为2，真实方位角分别为-40.17°和80.23°，真实俯仰角分别为50.30°和60.25°。设置信噪比为3 dB，对不同快拍数进行独立实验，结果如图4(a)所示。可以看出，与均匀矩形阵列情形不同，随着快拍数的增加，快速无格最大似然方法的均方根误差值不再明显减小，这是因为该情形下重构的特普利茨矩阵并不具有正定性，导致波达方向估计性能下降；低秩矩阵重构、原子范数最小化、GL-SPICE与文中方法的均方根误差值随着快拍数增加而减小，原子范数最小化与文中所述方法的均方根误差更接近克拉美罗界。

(2)不同信噪比的影响。设置快拍数为100，对不同信噪比进行独立实验，结果如图4(b)所示。可以看出，与不同快拍数情形相似，快速无格最大似然方法的均方根误差值随着信噪比增加不再明显减小，文中方法在大部分信噪比下均具有最小的均方根误差，更接近克拉美罗界。

(3)5个源信号的情形。其真实方位角分别为-100°、-50°、0°、80°和120°，真实俯仰角分别为50.34°、65.48°、55.95°、63.66°和60.25°。分别设置信噪比为9 dB和快拍数为200，对不同快拍数和信噪比进行独立实验，结果分别如图4(c)和(d)所示。可以看出，文中所述方法在大快拍数或高信噪比下的性能明显更好，能接近克拉美罗界。

(4)相邻源的影响。源信号与第3.1节相邻源实验一致。图4(e)显示了快拍数为200，信噪比为6 dB时，5种方法在不同方位角间隔下的仿真实验结果。可以看出，随着角度间隔的增大，5种方法的均方根误差均有所减小；快速无格最大似然方法需要方位角间隔不小于14°时，才有可以接受的均方根误差值，其他方法表现远优于快速无格最大似然方法；文中所述方法在角度间隔为4°时仍有很低的均方根误差，具有最好的相邻源波达方向估计性能。

(5)各算法的平均运行时间。使用上述5个源信号的设置，令快拍数为200，信噪比为9 dB，5种方法的200次平均运行时间如表1所示(计算机的CPU为英特尔i5-8500，内存的频率和容量分别为2 666 MHz和16 GB)。可以看出，快速无格最大似然方法的平均运行时间最短，文中方法运行时间最长，验证了节2.4的计算复杂度分析。

图4 稀疏矩形阵列下的均方根误差仿真实验结果

算法FGMLLRMRANMGL-SPICE文中方法平均运行时间/s0.020 20.161 50.212 50.192 10.415 9

4 结束语

笔者提出一种基于均匀矩形阵列或稀疏矩形阵列的二维无格波达方向估计方法。该方法使用样本协方差矩阵和log-det稀疏测度对相关的二阶特普利茨结构矩阵进行重构；然后通过二维ESPRIT方法进行二维波达方向估计。相比快速无格最大似然方法、均方根误差、原子范数最小化与GL-SPICE，文中方法能提供更稀疏的解，具有更好的波达方向估计性能，但计算复杂度相对较高。仿真实验中，笔者提出的方法具有在均匀矩形阵列和稀疏矩形阵列下的各情形中均具有很低的均方根误差，证明笔者提出方法良好的波达方向估计性能。在未来的研究中，可以考虑将该方法中使用的优化最小化算法替换为其他复杂度更低的优化算法，从而节省算法运行时间。