一种压缩型全姿态角四元数的表示方法

刘公绪，蔚保国，史凌峰，刘 洪，何 瑞，董亚军

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081；2．西安电子科技大学 电子工程学院，陕西 西安 710071)

用全姿态角来描述运载体在三维空间中任意位置的姿态，其概念普遍应用在导航、定位和制导等相关领域[1]。载体的姿态多用欧拉角表示，但欧拉角法具有奇异性，即当俯仰角为 ±90°时，会出现万向节锁，因而欧拉方程不能全姿态表示姿态角。学者们常借助欧拉角与四元数之间的转化进行运载体的全姿态表示[2-3]。姿态四元数的表示问题通常包括姿态空间的描述问题，以及姿态角与四元数的映射问题，它们是姿态估计和控制算法的基石[4-7]。在用四元数表示运载体姿态时，虽然四元数可以有效避免姿态角的奇异问题，但四元数的状态空间对姿态角空间是双重覆盖的，即对任意一组姿态角，都有两组四元数与之对应，这会导致在姿态控制时出现姿态散开问题[8,9]。姿态散开是指四元数的二重覆盖性会在两组四元数向量的邻域形成一个吸引域和一个排斥域，导致当初始条件接近平衡点时会忽然反方向绕开去，绕一整圈后再回到平衡点。为解决这一问题，笔者提出一种压缩型全姿态角四元数的表示方法。其基本思想如下：运载体的实际姿态可分别惟一用姿态角空间和四元数空间进行描述，从这个角度讲，姿态角空间和四元数空间都不应该是冗余的，应该是压缩的，即包含且仅包含运载体的实际姿态信息。因此引入压缩型姿态角空间和压缩型四元数空间两个概念，并通过方向余弦矩阵与四元数的转化关系实现两个压缩空间的一一映射，并且两个压缩空间都与运载体的实际姿态一一对应。最后通过数值仿真实验验证了所提出方法的可行性。

1 压缩型姿态角空间

这里采用东-北-天坐标系为导航坐标系(n系)。起初，载体坐标系(b系)与导航坐标系重合，运载体的右前上各自指向东-北-天方向。载体绕X,Y,Z轴旋转分别得到俯仰角(θ)，横滚角(φ)和航向角(ψ)，如图1所示。关于姿态角的扩展在学术研究或工程应用中并没有明确规定，原则上需要表示运载体在三维空间中的全姿态。在压缩型姿态角空间中，对其中任意一个姿态角进行压缩均可以实现对运载体实际姿态信息的唯一描述。考虑到在方向余弦矩阵中，决定俯仰角大小的只有一项，对其扩展会增加难度，而决定另外两个姿态角大小的都各有两项，对其扩展相对容易。因此采取对俯仰角压缩，即不扩展，而对横滚角和航向角进行扩展的处理方法为

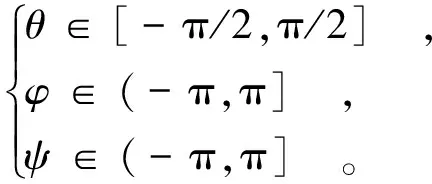
(1)

为方便描述，将式(1)称为压缩型姿态角空间。

关于式(1)对运载体全姿态唯一描述的机理做如下说明。这里俯仰角的取值范围是[-π/2, π/2]，若只考察俯仰角，显然其二、三象限与一、四象限是叠加在一起的，具有二义性，不能描述俯仰角的全姿态，关于坐标系象限的定义见图2。若整体考察运载体的三个姿态角的取值，可以发现俯仰角在±π/2时，横滚角和航向角也会发生180°的相位变化。因此，完全可以综合考察三个姿态角的大小来惟一确定运载体在导航坐标系中的姿态。下面将介绍如何对传统四元数空间进行约束，构造压缩型四元数空间，消除四元数对姿态角的二重覆盖性。

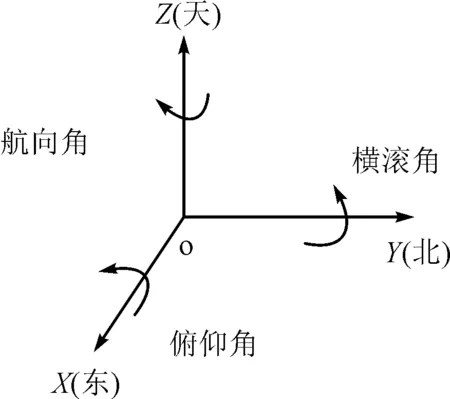
图1 坐标系示意图及姿态角的定义

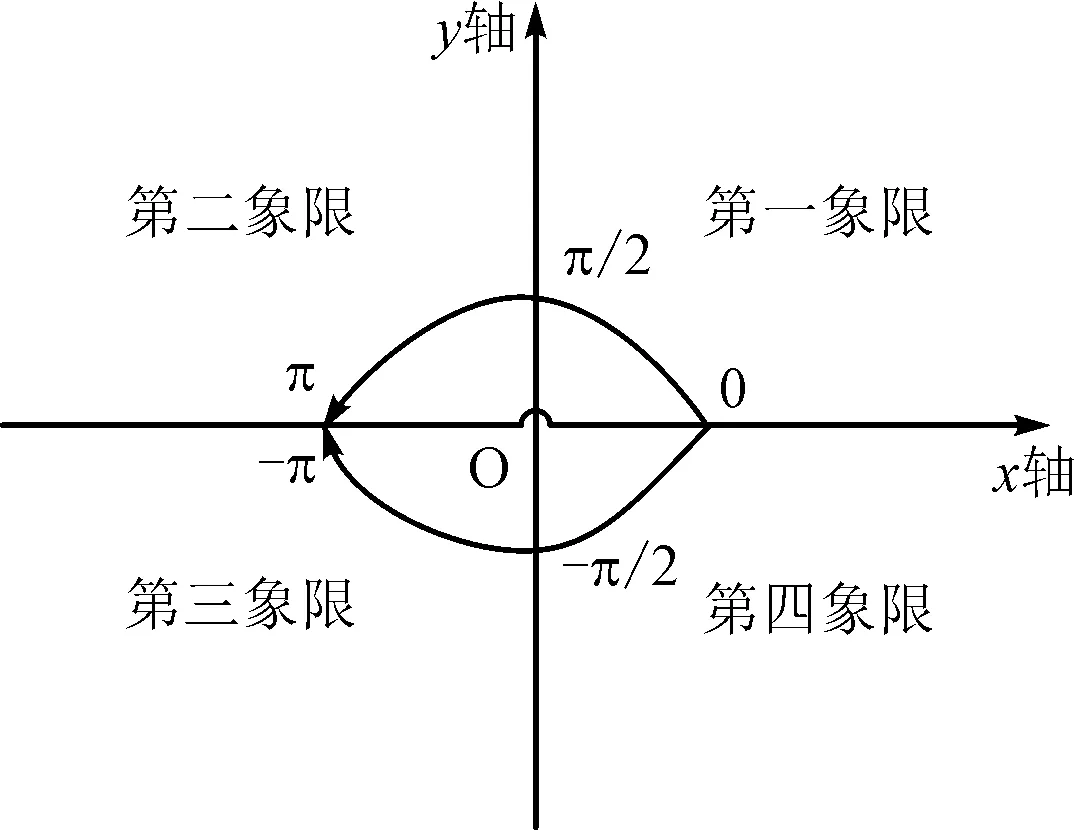
图2 坐标系的象限

2 压缩型四元数空间

在图1中，绕坐标系X, Y, Z轴分别作基本旋转,可得到相应的坐标变换矩阵，如式(2)～(4)所示[10]:

(2)

(3)

(4)

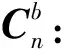
(5)

从载体坐标系到导航坐标系的姿态转换矩阵:

(6)

rn=q⊗rb⊗q*,

(7)

其中，⊗表示四元数乘法。与姿态转换矩阵类似，上式可转化为

(8)

(9)

依次绕X, Y, Z轴做基本旋转，得到四元数表示分别为

(10)

(11)

(12)

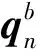
(13)

根据导航坐标系与载体坐标系的转换关系，可以得到从载体坐标系到导航坐标系的四元数变换矩阵:

(14)

对式(14)展开，得到由姿态角转化到四元数的方程组如下：

(15)

结合式(6)和式(9)，可以得到由四元数转化为姿态角的方程组[12]：

(16)

联合压缩型姿态角空间式(1)，式(15)和四元数模值约束条件，可得出四元数空间取值为

(17)

事实上，约束后的四元数空间式(17)仍不能完全消除二重覆盖性，因此，对四元数空间进一步压缩，得到压缩型四元数空间为

(18)

显然压缩的形式有多种，这里不再一一列出。

至此，已经阐明了压缩型姿态角空间和压缩型四元数空间。下面即进行数值仿真实验，验证所提出方法的可行性。

3 数值仿真和分析

3.1 姿态角奇异性测试

当俯仰角为±π/2时会出现奇异问题，这里对姿态角奇异性测试的方法如下。使俯仰角在-π/2与π/2之间交替变化，使横滚角和航向角在(-π,π]内随机变化，用来模拟当俯仰角为±π/2时，任意横滚角和任意航向角下姿态角的奇异情况。若所提的方法具有奇异性，则解算的四元数是无穷多组解中的一组，可以通过四元数与姿态角之间的转换关系反解算四元数得姿态角，然后对比前后姿态角的误差。若出现奇异问题，则意味着在反解算时，作为输入的是无穷多组解中的一组解，得到的姿态角与生成的姿态角完全相等的概率几乎为零，则反解算前后姿态角误差势必较大，否则误差很小。因此可以通过生成姿态角与反解算姿态角的前后误差来判断是否出现奇异性问题。测试结果如图3所示，可见误差在10-11量级，误差主要来源是弧度与角度之间转换时导致的误差，以及四元数归一化时导致的截断误差。该实验验证了压缩型四元数空间继承了四元数表示姿态角的非奇异性优点。

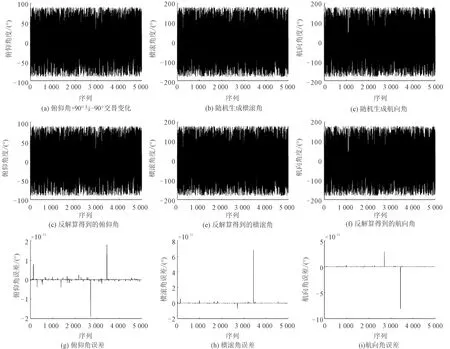
图3 姿态角奇异性测试

3.2 两个压缩空间的一一映射关系验证

为了验证压缩型姿态角空间与压缩型四元数空间的一一映射关系，开展了以下实验，如图4和图5所示。首先随机生成压缩型姿态角空间，然后根据式(15)将姿态角映射到压缩型四元数空间，再根据式(16)，将映射的四元数反映射到压缩型姿态角空间，将得到的姿态角与生成的姿态角做差，即得到误差。由图4可见误差在10-11量级，误差主要来源是弧度与角度之间转换时导致的误差，以及四元数归一化时导致的截断误差。接着随机生成压缩型四元数空间，根据式(16)将四元数映射到压缩型姿态角空间内，再根据式(15)，将得到的姿态角反映射到压缩型四元数空间内，最后将得到的四元数与生成的四元数做差，即得到误差。由图5可见误差在10-15量级，误差主要来源同上述分析。

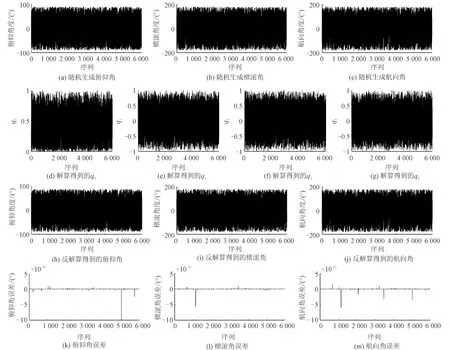
图4 压缩型姿态角空间与压缩型四元数空间的一一映射关系验证

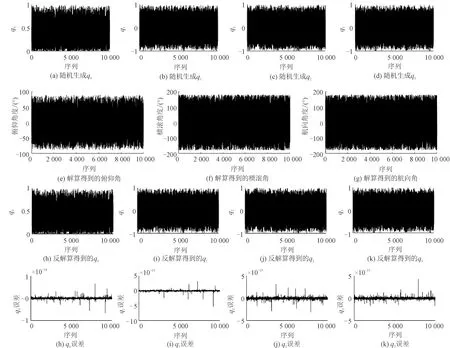
图5 压缩型姿态角空间与压缩型四元数空间的一一映射关系验证

4 结束语

针对传统姿态角空间与四元数空间的非一一映射关系而引起的姿态散开等问题，首先引入压缩型姿态角空间和压缩型四元数空间两个概念，提出一种新颖的压缩型全姿态角四元数的表示方法。基于压缩型姿态角空间的概念，分析了姿态角的压缩过程及压缩姿态角空间对运载体全姿态唯一描述的机理；基于压缩型四元数空间的概念，通过增加四元数空间的约束条件，消除四元数的二重覆盖性；并通过方向余弦矩阵与四元数的相互转化关系实现两个压缩空间的一一映射。然后通过数值仿真实验验证了所提出方法的可行性。测试结果表明该方法可以唯一表示运载体在三维空间中的全姿态信息，无奇异性问题，无姿态散开问题，可以普遍应用在导航、制导等领域，具有一定的科学研究价值和工程实践意义。文中所述的姿态描述方法消除了四元数对姿态角的二重覆盖性，但四元数的二重覆盖性在某些算法中有一定作用，如基于旋转矢量的姿态估计方法，它利用四元数的二重覆盖性，减少了刚体旋转的不可交换误差。因此在实际应用中，应根据笔者提出的压缩映射思想，选择合适的坐标系进行姿态描述，然后利用相关的姿态解算和控制算法达到预期目的。