一种利用声音能量的两步SDR定位算法

田 强，冯大政，李 进，胡豪爽

(1.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071；2.西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

无线传感器网络定位技术在雷达、无线通信、麦克风阵列等领域[1-3]有着广泛的应用。目前无线定位技术主要包括基于到达时间定位、基于到达时间差定位、基于到达角度定位以及基于声音能量定位[4-7]。其中，基于声音能量定位只需要传感器对接收到的信号样本加和求平均即可获得定位测量数据，不需要传感器之间进行复杂的时间同步，具有操作简单、成本低的优点，因而受到了越来越多的关注。

根据声音能量衰减模型[8]，利用声音能量数据对目标进行定位本质上是一个非线性、非凸的参数估计问题。最大似然估计提供了非线性问题在统计意义下的最优解。然而其需要进行迭代求解，且迭代过程依赖于初始值的选取；当初始值选取不好时容易陷入局部极小点，难以得到令人满意的解。为了解决这一问题，目前主要采用的方法包括闭式解算法[8-10]和凸优化方法[11-12]。闭式解算法能够避免迭代运算，具有计算复杂度低的优势。其中，文献[8]通过消除二次项，将定位问题转化为无约束最小二乘估计，得到目标位置的闭式解；但实验结果表明该方法定位精度较差。文献[9]和文献[10]通过引入不同的辅助变量来克服非线性问题，分别提出了加权最小二乘(Weighted Least Squares, WLS)算法和基于校正技术的加权直接最小二乘(Weighted Direct least squares solution with Correction, WDC)算法。以上两种方法在定位性能上均优于文献[8]中的算法，且在量测误差较小时可以逼近克拉美罗界(Cramér-Rao Lower Bound，CRLB)；然而由于这两个方法在推导过程中忽略了二阶误差项，因此当测量误差较大时，定位精度会严重下降。与闭式解方法不同，凸优化方法是利用凸松弛(Convex Relaxation, CR)技术将原非凸的定位问题转化为半正定规划(Semi-Definite Program, SDP)[11]或二阶锥规划(Second Order Cone Program, SOCP)[12]等凸优化问题进行求解，其优点是迭代过程不依赖于初始值的选取并且能够保证全局收敛性；但是这类方法对代价函数的松弛变换在多数情况下不是紧的，容易造成性能损失。

基于声音能量的定位模型涉及目标位置和信号发射能量两个未知变量。需要指出的是，虽然量测数据对于目标位置是非线性的，但是对于信号发射能量是线性函数。现有的大多数算法忽略了这一特性，而是将这两个未知变量进行联合估计。为了充分利用上述特性，笔者将原问题近似为一个加权最小二乘问题，通过对两个未知变量分别进行求解，提出了一种两步半正定松弛定位方法。该方法首先将信号发射能量表示成关于目标位置的函数，并在代价函数中将其替换消除掉；然后利用新的凸松弛技术将新得到的代价函数转化为半正定规划问题进行求解。

1 定位模型

考虑文献[8-11]中所采用的声音能量衰减模型。假设在二维平面内分布了M个传感器锚节点，其坐标已知且表示为si=[xi,yi]Τ,i=1,2,…，M；待估计的目标节点坐标假设为x=[x,y]Τ。根据能量衰减模型，第i个传感器接收到的声音能量数据为

(1)

由式(1)可得关于目标位置x和信号发射能量P的最大似然估计等价于最小化如下代价函数：

(2)

优化求解式(2)即可得到未知变量x与P的估计值。然而，式(2)中的代价函数是非线性、非凸的，难以直接求解。下面将原定位问题转化为近似加权最小二乘估计，并提出两步半正定松弛算法进行优化求解。

2 算法描述

2.1 近似加权最小二乘估计

将式(1)中的ni移到方程等号左边，对两边进行开方运算，然后求取倒数，经整理可以得到：

(3)

式中zi是已知常量，则式(3)左边可以看成是关于随机变量ni的函数。由于ni相比于zi和P很小，且均值为零，对式(3)左边在ni=0处进行一阶泰勒展开，经进一步整理，可近似得到：

(4)

(5)

(6)

为了简单起见，令P′=P1/2，则式(6)可以等价地转化为如下最小化问题：

(7)

2.2 两步半正定松弛算法

2.2.1 消除变量P′

在式(7)中，固定目标位置x，单独求解变量P。将式(7)中的代价函数对P求导，并令导数等于0，易得P′关于x的解析表达式为

(8)

(9)

可以看到，式(9)的代价函数中只包含未知变量x，但其依然是非线性、非凸的，下面利用新的凸松弛技术将其转化为半正定规划问题。

2.2.2 半正定松弛

(10)

(11)

注意到，优化问题(11)中的代价函数是凸的，但其中的两个约束条件依然非凸。首先考虑非凸约束di=‖x-si‖2。定义辅助变量u=xΤx，结合矩阵D的定义，此约束条件可写成

(12)

式中，Dii表示D的对角元素。此外，根据柯西-施瓦兹不等式，D的非对角元素满足

(13)

式中|·|表示绝对值运算。接下来考虑非凸约束D=ddΤ。根据半正定松弛理论[13]，此约束条件等价于

(14)

(15)

由于约束rank(D)=1是非凸的，在问题(15)中将矩阵D的这个“秩-1约束”直接去掉，同时将u=xΤx松弛成u≥xΤx；此时，原非线性、非凸的目标定位问题最终转化为如下半正定规划问题：

(16)

显然，问题(16)是一个凸优化问题，通过调用凸优化工具包(CVX)[14]很容易对其进行优化求解，最终得到目标位置的估计值。

值得注意的是，虽然在对式(15)的松弛过程中直接忽略了矩阵D的秩-1约束，但下面的定理表明在求解问题(16)时得到的矩阵D的估计值总是满足秩等于1。

定理1 假设{D*,d*,x*,u*}是式(16)的最优解，则D*的秩总是等于1的，即rank(D*)=1。

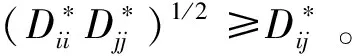
(17)

(18)

根据D′的定义，显然{D′,d*,x*,u*}是满足式(16)的一组可行解。而{D*,d*,x*,u*}是最优解，则有

tr(AD*)≤tr(AD′) 。

(19)

对比式(18)和式(19)，可以得到D*=D′。由D′的定义可知，其秩是等于1的，因此rank(D*)=1。 证毕。

根据定理1及其证明可以看出，文中算法对矩阵D的松弛近似是紧的。

3 算法性能评估

下面通过仿真实验与文献[9]中的基于校正技术的加权直接最小二乘(WDC)算法、文献[10]中的加权最小二乘(WLS)算法、文献[11]中的半正定松弛(SDR)算法以及克拉美罗界(CRLB)[10]进行对比，详细评估了文中算法的定位性能(由于文献[12]中的二阶锥规划算法假设P是先验已知的，与笔者提出的定位模型不同，因此这里不做对比)。在实验中，半正定松弛(SDR)和文中算法都用凸优化工具包(CVX)进行优化求解。

图1 不同测量误差下的各算法性能对比图

图2 各算法的误差累积分布函数

图3表示各算法的定位性能随传感器节点数目变化的统计结果。可以看到，随着传感器节点数目的增多，由于可以提供更多冗余测量数据，各算法的定位精度均有所提高，而WLS算法变化却很不明显。文中算法的位置估计均方根误差一直保持最低，定位性能优于其他参考算法。

图3 不同传感器数目下各算法性能对比图

图4 衰减因子偏差对各算法性能的影响

图4描述了各算法的估计均方根误差随衰减因子偏差的变化曲线。从图4中可以看出，随着衰减因子偏差的增大，由于定位模型失配的原因，所有算法的定位精度都有所下降。其中，WLS算法对衰减因子偏差最为敏感；而文中算法的性能始终保持最优，说明文中算法对衰减因子偏差的容忍度较高。

4 结束语

针对基于声音能量定位存在的非线性问题，笔者提出了一种两步半正定松弛算法。先利用定位模型对于信号发射能量是线性函数这一特性，将信号发射能量从代价函数中消除；然后利用凸松弛技术将原定位问题转化为半正定规划问题进行求解。从理论上证明了文中的松弛近似过程是紧的。仿真结果表明，该算法的定位性能优于传统的闭式解算法以及凸优化方法，尤其在测量误差较大时具有明显的优势。