数据驱动的GMC稀疏增强诊断方法

陈保家，贺王鹏，胡 洁，王 赓，郭宝龙

(1.三峡大学 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002;2.西安电子科技大学 空间科学与技术学院，陕西 西安 710071)

大型复杂机械设备的状态监测与故障诊断理论与技术一直是国内外的研究热点。如果能在机械设备故障的初期阶段识别故障，并及时采取有效措施进行维护，对于保障设备运行安全具有重要意义[1-2]。然而在机械设备诊断过程中，无论是在时域还是在频域上采集得到的振动信号总是包含着噪声干扰成分[3]。因此，如何精确提取微弱故障特征是大型复杂机械设备的状态监测与故障诊断领域所面临的巨大挑战[4]。

信号稀疏表示方法是强噪声干扰下提取微弱故障特征的有效方法之一，基于l1范数的凸正则化是目前应用最为广泛的稀疏表示方法，不仅能够有效地诱导稀疏，而且利用l1范数方法所建立的目标函数具有严格凸性，可很容易利用算法得到全局最优解。但l1范数方法容易低估被提取信号的高振幅分量，而振动峰值信号往往可能包含着更多的故障特征信息。非凸正则化也得到了广泛的应用，对高振幅分量的估计更为准确的同时，还可以提取出更为稀疏的故障特征。然而，非凸正则项的引入可能会牺牲目标函数的严格凸性，使其具有不相关的局部极小值。针对此问题，一些学者在近年来研究了能够保持目标函数整体为凸的非凸稀疏正则化凸优化问题，且所得结果比凸稀疏正则化更佳[5]。文献[6]采用非凸精细正则化用于增强特征稀疏性，有效地解决了轴承故障诊断中耦合稀疏故障特征分离的问题。文献[7]提出了一种基于非凸稀疏正则化的齿轮箱故障特征提取方法，解决了从噪声数据中同时提取周期瞬态和高共振分量用于齿轮箱故障检测的问题。文献[8]提出了一种针对轴承的故障诊断方法，采用非凸正则项来增强特征的稀疏性，该方法有效地提高了轴承故障信号的估计精度。文献[9]提出了一种功率分配算法用于多站分布式雷达的目标定位，对凸松弛算法加以改进，通过凸松弛参数的自修正减少凸松弛算法的额外误差来逼近最优结果。

笔者提出了一种数据驱动的广义最小最大凹(Generalized Minimax-Concave，GMC)惩罚函数增强的稀疏特征提取方法。该稀疏特征提取方法是利用广义最小最大凹惩罚函数建立优化问题目标函数，以提高故障特征的提取精度，并且证明了保持目标函数整体为凸所需要满足的约束条件。引入近端算法求解所构造的无约束优化问题。此外，笔者研究了数据驱动的正则化参数设置准则，保证所提出的稀疏特征提取方法具有参数自适应性。将该方法应用于仿真信号和实际故障实验中，结果表明，所提出的方法可以精确地从噪声干扰中提取出微弱故障特征且效果更稀疏。

1 信号模型和广义最小最大凹惩罚函数

1.1 信号模型

假设观测到的信号y的表达式为

y=x+w，

(1)

其中，x表示故障信号，是由局部故障引起的重复瞬态；w表示背景噪声，一般为高斯白噪声和其他不需要的分量。

1.2 广义最小最大凹惩罚函数

在文中，广义最小最大凹惩罚函数用来加强特征的稀疏性[10]。广义最小最大凹惩罚函数是利用由卷积下确界定义的Huber函数进行多元推广得到的，是一类能够确保最小二乘目标函数严格凸性的非凸罚函数，既避免了传统l1范数正则化求解算法问题的低估特性，又能更大限度地增强提取特征的稀疏性[5]。

一般，变尺度Huber函数可定义为

sb(x):=s(b2x)/b2,b≠0 ，

(2)

(3)

根据Huber函数，定义最小最大凹惩罚函数：

(4)

因此，一元变尺度惩罚函数(最小最大凹惩罚函数)可定义为

φb(x)=|x|-sb(x) 。

(5)

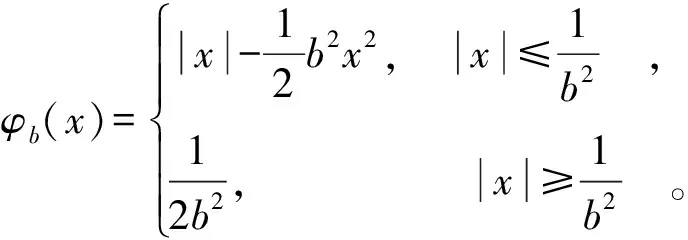
若存在矩阵B，则可得到Huber函数的多元推广sB(x)，其表达式为

(6)

对应的最小最大凹惩罚函数多元推广(即广义最小最大凹惩罚函数)的表达式为

ψB(x)=‖x‖1-sB(x) ,

(7)

其中，sB(x)为Huber函数的多元推广。图1为广义最小最大凹惩罚函数ψB(x)的曲线。

图2 惩罚函数的非凸程度与参数大小之间的关系

文中调节参数b或矩阵B可实现对广义最小最大凹惩罚函数非凸程度的控制。若标量参数b≥0，则矩阵B满足半正定。改变参数大小，广义最小最大凹惩罚函数非凸程度的变化情况如图2所示[11]。通过观察图2可发现，随着参数b值的增大，惩罚函数的非凸程度加大，提取特征的稀疏性也在不断加强。

2 稀疏信号优化特征提取算法

针对稀疏故障特征提取精度低的难题，笔者提出一种数据驱动的广义最小最大凹惩罚函数增强的稀疏特征提取方法。具体包括稀疏优化问题的构造、目标函数为凸的约束条件、快速收敛算法流程以及正则化参数的自适应准则。

2.1 优化问题的构造

基于稀疏增强的广义最小最大凹惩罚函数，构造如下无约束优化问题：

(8)

其中，F为无约束优化问题的目标函数;y∈RN,为观测到的含噪信号。

2.2 目标函数为凸的约束条件

所建立的优化问题目标函数整体的严格凸性，可通过控制广义最小最大凹惩罚函数的非凸程度来实现，其理论依据为：目标函数中的第1项为二次项具有严格凸性，因此通过对广义最小最大凹惩罚函数中的非凸可控化参数进行控制，调整广义最小最大凹惩罚函数的非凸程度以确保目标函数F的整体凸性。故在用近端算法求解该优化问题时，最终结果迭代收敛于全局最优解，且不会受不相关的次优局部极小值的影响。

定理1设y∈RN，λ>0。则式(8)中F为凸函数时应满足[10]：

(9)

其中，B可以设置为

(10)

2.3 基于近端算法的快速收敛算法

(11)

鞍点问题是单调包含问题的实例，因此可通过前向-后向算法(Forward-Backward Algorithm，FBA)计算得到[11]。具体算法步骤如下：

输入：y∈RN,,。

初始化：ρ=max{1,γ/(1-γ)}, 0<μ<2/ρ。

对i=0,1,2...执行循环：

(1)ω(i)=x(i)-μ(I(x(i)+γ(v(i)-x(i)))-y)。

(2)u(i)=v(i)-μγ(v(i)-x(i))。

(3)x(i+1)=soft(w(i),μλ)。

(4)v(i+1)=soft(u(i),μλ)。

直至收敛。

输出：x。

2.4 正则化参数自适应准则

图3 正则化参数λ随噪声标准差σ的变化情况图

这里研究数据驱动的正则化参数设置准则，保证所提出的稀疏特征提取方法具有参数自适应性。由于背景噪声大小的不同，目标函数中的正则化参数λ的取值也不同。对于不同大小的噪声，都存在着最优的正则化参数λ，使得稀疏故障特征的提取达到最好的效果。因此，可根据噪声标准差σ的大小，设置广义最小最大凹惩罚函数构造的目标函数的正则化参数λ。在实践中，为了加强特征的稀疏性使提取结果达到最佳稀疏效果，惩罚函数中的非凸可控化参数一般设置为γ=0.8。经过大量的数值模拟，统计得到噪声标准差σ与正则化参数λ的关系与拟合直线如图3所示。通过该拟合直线，对于不同噪声干扰可以自适应地对正则化参数进行设置。

3 数值模拟信号验证

在本节中，仿真研究所提出的广义最小最大凹惩罚函数增强的稀疏特征提取方法在故障特征提取方面的性能，模拟一组冲击信号并加入高斯白噪声n(t)以模拟背景干扰噪声。其中单个冲击信号的表达式为

x(t)=exp(-20t)sin(100t) ,

(12)

仿真信号的表达式为

y(t)=Ax(t)+n(t) ,

(13)

其中，A表示冲击信号的幅值。图4(a)为模拟的冲击信号波形，含噪的模拟信号波形如图4(b)所示，其中fs=1 000 Hz作为采样频率，选取信号分析长度M=10 000以及添加的噪声其标准差σ=0.08。图4(b)中，模拟的冲击信号被强烈的背景噪声所破坏，无法识别和观测到脉冲特征及故障特征频率。选用均方根误差(Root-Mean-Square Error，RMSE)[12]对其进行性能评估，对于图4(b)中的含噪仿真信号，其均方根误差为0.096 5。

图4 仿真信号波形及特征提取结果

利用文中所提出的方法对该含噪仿真信号进行处理，所得到的特征提取结果如图4所示，其中加入了l1范数正则化方法以供对比，正则化参数设置λ=0.23。结果表明，与l1范数正则化方法相比，所提出的方法能够在降低背景噪声的同时保留冲击信号的幅值，其均方根误差为0.072 2，而l1范数正则化方法的均方根误差为0.080 6。

4 实际信号验证

为验证所提出的广义最小最大凹惩罚函数增强的稀疏特征提取方法在机械故障识别中的有效性，将其应用于识别某轨道交通实验台的滚动轴承外圈轻微损伤故障。轴承安装在测试实验装置上，测试采样频率为12.8 kHz，转速约为481 r/min。通过滚动轴承具体参数，计算得到其外圈故障对应的理论特征频率为fo=57.8 Hz[13]。

图5(a)为采集到的轴承外圈故障信号时域波形，通过观察可以发现，时域信号中干扰噪声比较大，观察不到清晰的故障冲击特征。针对实际测量得到的信号，背景噪声的标准差σ可以由基于小波基去噪的绝对中位差方法进行估计得到[14]。此数据估计得到的背景噪声标准差σ=0.164 8，据此自适应设置正则化参数为λ=0.48。如图5(b)所示，所提出的方法能够有效地降低背景噪声且保留冲击信号的幅值，明显地观察到所有的故障冲击特征，冲击单元的时间间隔约为17.2 ms，对应特征频率为58.1 Hz，与计算得到的外圈故障理论特征频率fo=57.8 Hz基本一致。

图5 实际信号波形及特征提取结果

5 结束语

笔者提出了一种数据驱动的广义最小最大凹惩罚函数增强的稀疏特征提取方法。该方法能够在保留故障特征频率的同时很好地消除背景噪声干扰成分。利用所提出的方法建立的无约束优化问题目标函数可有效地提高特征的提取精度，广义最小最大凹惩罚函数的非凸性用于加强故障特征的稀疏性。此外，证明了广义最小最大凹惩罚函数保证目标函数整体为凸所需满足的约束条件。引入近端算法求解基于广义最小最大凹惩罚函数的优化问题，该算法最终收敛于全局最优解。通过RMSE指标，定量地分析了所提出的数据驱动的广义最小最大凹惩罚函数增强的稀疏特征提取方法，在仿真信号中的正确性及有效性。最后，将所提出的方法通过实验和实际应用对轴承故障进行诊断，结果表明，该方法可有效地识别出滚动轴承外圈轻微损伤故障。