利用判别字典学习的视觉跟踪方法

王洪雁，邱贺磊，裴腾达

(大连大学 信息工程学院，辽宁 大连 116622)

目标跟踪是计算机视觉领域的研究方向之一，其在视频监控、自动驾驶、人机交互等方面具有广泛应用。近年来，视觉跟踪方法取得显著进步，许多高效、鲁棒的跟踪算法被提出[1-3]。然而，许多具有挑战性的问题仍未得到有效解决，如光照变化、尺度变化、遮挡及背景杂波等，从而导致跟踪算法的性能显著下降。

为改善复杂场景下视觉跟踪性能，WANG等[4]提出用于模板更新的非负字典学习方法，将最近所得跟踪结果融合以产生鲁棒性较好的模板，进而利用该模板实现目标精确跟踪。然而，当存在复杂的背景杂波时，该算法难以有效地区分目标与相似背景。针对此问题，XIE等[5]对目标及邻近背景的外观信息编码，利用样本训练判别模型提高字典的判别能力，改善跟踪性能。然而，由于目标及邻近背景位置选取的样本存在共同特征，从而导致字典的判别能力显著降低。针对此问题，WEN等[6]同时利用类内信息和类间相关性学习类内和共享字典，则类内字典具有较强的独立性，使得所构建字典具有较强的判别能力。然而，该算法未考虑遮挡或噪声等干扰，使其易受异常值影响而导致跟踪漂移。基于此问题，SUI等[7]构造子空间表示目标及邻近背景，并提出一种判别准则以提高字典的判别能力。此外，该方法使用稀疏误差项补偿损坏样本以提高算法对遮挡或噪声等的鲁棒性。然而，该方法使用有偏的l1范数惩罚误差矩阵，其可能过度惩罚较大变量而导致优化问题获得次优解[8-10]，进而影响目标跟踪精度。针对此问题，文献[10]利用近乎无偏的极大极小凹加函数惩罚误差矩阵，以克服l1范数对误差矩阵不平衡惩罚。然而，该非凸约束方法并未被有效应用于视觉跟踪领域。

针对上述问题，笔者提出一种目标跟踪方法。该方法考虑了目标的时空局部相关性。时间局部相关表明目标之间在时域上具有显著局部相关性；空间局部相关表明背景与目标的空间距离越近，目标与背景的相关性越强。基于此，根据最近若干帧的跟踪结果选取目标样本，并在目标位置周围采样确定背景样本。针对目标及背景字典中具有共同特征的原子，在判别字典学习模型中施加字典不一致约束项，使目标及背景字典更具独立性，从而提高字典的判别能力。针对遮挡或噪声等问题，在所提算法中加入可捕获异常值的误差项以有效减少异常值影响，从而提高算法的鲁棒性。另外，使用极大极小凹加范数惩罚稀疏编码矩阵和误差矩阵，以避免对一些较大变量过度惩罚而导致次优解，提高目标跟踪精度。针对所构建的非凸判别字典优化问题，使用基于优化最小化(Majorization-Minimization, MM)的不精确增广拉格朗日乘子(Inexact Augmented Lagrange Multiplier, IALM)方法求解该问题，以获得较好的收敛性。基于所得最优判别字典计算候选目标的重构误差以构建目标观测模型，并基于贝叶斯推理框架以实现目标的精确跟踪。

1 判别字典学习算法

首先描述所提判别字典学习模型，而后介绍所得非凸判别字典优化问题的求解方法，并分析算法的收敛性及计算复杂度，最后给出初始化方法及字典更新方法。

1.1 判别字典学习模型

给定训练样本集Xi∈Rd×qi,i=1,2，其中d表示各训练样本的特征维度，qi为第i类训练样本集的数量。根据训练样本集学习得到字典Di∈Rd×ki，其中ki表示第i类字典的原子数量。Ci∈Rki×qi，为第i类训练样本集Xi在字典Di上的编码系数矩阵。基于稀疏表示理论，应有Xi≈DiCi，则基本字典学习模型为

(1)

由于训练样本中难免存在遮挡或噪声等问题，导致当前训练样本中存在异常值，进而降低字典学习算法的鲁棒性。针对此问题，在字典学习模型中加入误差项以捕捉这些异常值，即

(2)

其中，Pi为误差矩阵，β为正则化参数。易知，式中的l0范数优化问题为NP-hard问题，通常使用l1范数松弛处理[4-5,7]。然而l1范数为有偏估计量，其可能会对较大变量过度惩罚。针对此问题，采用非凸极大极小凹加函数代替l0范数以获得近乎无偏估计[8-10]。首先给出极大极小凹加函数定义。

设向量a=(a1,a2,…,ap)T∈Rp，当υ>0，γ>1时，MCP惩罚函数表示为

(3)

其中，(u)+=max{u,0}。设A为矩阵，将矢量极大极小凹加函数扩展到矩阵形式[8-9]，表示为

(4)

为便于表述，令Jγ(A)=J1,γ(A)，Mγ(A)=M1,γ(A)，则当γ→时，Jγ(A)→|A|，其为对应l1范数的软阈值算子；当γ→1时，其为对应l0范数的硬阈值算子[10]。设γ∈(1,)。

利用极大极小凹加函数代替式(2)中l0范数，则字典学习模型可表示为

(5)

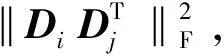
综上所述，判别字典学习模型可构建为

(6)

其中，i=1,2,j=1,2,j≠i，λ为正则化参数。

1.2 所提模型优化方法

由于模型(6)中极大极小凹加函数非凸，因而所提字典学习模型为非凸优化问题，不能直接采用凸优化方法求解。受ZHANG等[8]所提求解方法启发，基于MM-IALM方法求解所得非凸判别字典优化问题。该方法包含内环和外环。每次迭代中，外环用局部线性近似来逼近原非凸问题以将其转化为加权凸优化问题；内环则采用不精确增广拉格朗日乘子法求解该问题以将其最小化，多次迭代求解可逼近原目标函数最优解。

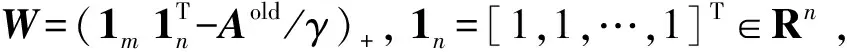
Dτ,W(H)=sign(Hmn)(|Hmn|-τWmn)+，

(7)

其可看成问题(8)的闭环解

(8)

给定Aold，则问题(8)中Qγ(A|Aold)即为Mγ(A)的局部线性近似，可表示为

(9)

基于以上所述算法，给出所提非凸判别字典优化问题的求解方法，如下所述。

外环为减少计算量，采用一步局部线性近似方法，即只运行外环一次[8-9]，而非等待收敛或达到最大迭代次数。实验表明，采用多步局部线性近似方法(即等待外环收敛)只比一步局部线性近似有微小提升，但运算量较大。

基于式(9)，利用代理函数Qγ(Ci|Coldi)及Qγ(Pi|Poldi)分别替代Mγ(Ci)和Mγ(Pi),得式(6)的上界函数:

(10)

内环使用不精确增广拉格朗日乘子方法求解问题，注意到问题中第一个约束项关于Di和Ci乘积耦合。为利用形如式(7)的闭环解求解变量Ci，需引入辅助优化变量Bi=Ci，则式(10)等价为

(11)

利用拉格朗日乘子法将约束优化问题转化为无约束优化问题，则目标函数可写为

(12)

其中，Vi为拉格朗日乘子；μi>0，为惩罚参数。问题的求解可分为若干个子问题:

(13)

已知式(7)为问题(8)的解，则可得式(13)中关于变量Bi和Pi的子问题的解。已知式(13)中关于变量Ci和Di的子问题为凸问题，根据矩阵微分知识，可得关于变量Bi和Pi的子问题的解。式(13)的解分别表示如下:

(14)

其中，I∈Rki×ki,为单位矩阵。WBi和WPi的初始化方法详见表1。

根据式(14)，在第q+1次迭代中，依次更新各变量，然后更新Vi和μ1：

(15)

重复上述过程，直至满足收敛条件(收敛条件见算法1)。关于问题(6)的整体求解算法如算法1所示。

算法1MM-IALM方法解决问题(6)。

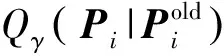
(4) 重复以下4步，直至收敛：

④q=q+1；

(5) 输出：Di。

1.3 收敛性和计算复杂度分析

收敛性和计算复杂度是评价优化算法优劣的两个标准，本小节分别从这两个方面分析所提优化算法。

1.3.1 收敛性分析

所提字典学习模型非凸，因此难以给出全局收敛的严格数学证明，但其存在局部收敛性[8-9]。如上所述，MM-IALM优化方法在外环使用一步局部线性近似方法逼近原非凸问题，即只运行外环一次，则该优化方法的收敛性主要取决于内环。基于式(9)，目标函数在每次迭代中满足如下引理。

(16)

由式(16)可知目标函数f(Di,Ci,Pi)单调非递增，则MM-IALM优化算法具有局部收敛性。此外，ZHANG[8]和LI[9]的研究表明，该非凸问题的局部最优解通常优于凸松弛所得问题的全局最优解。

1.3.2 计算复杂度分析

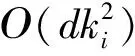
1.4 初始化和字典更新

1.4.1 初始化

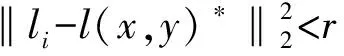
1.4.2 字典更新

为确保所提方法能适应目标外观变化，笔者在线更新字典Di。由于第1帧中手动选择目标，因此首帧目标始终真实。在整个字典学习过程中始终保留首帧获取的训练样本集X1以缓解漂移问题。为获得更具鲁棒性和判别性的字典，算法从连续T帧中收集目标及背景样本，并设置样本池Xtrain和临时样本池Xtemp。Xtemp={Xt-T+1,Xt-T+2,…,Xt}，表示从前T帧收集的所有训练样本，Xt表示根据第t帧跟踪结果收集的训练样本，从而得到一个样本池Xtrain={X1,Xtemp}。使用样本池Xtrain即可学得新字典Di以用于跟踪下一帧中的目标。获得最优判别字典后需清空Xtemp，以收集新的训练样本。

在样本收集过程中，当样本积累到Xtemp中时，跟踪结果可能包含遮挡或噪声等干扰。若跟踪器确定的目标最优位置的评估值(评估方法见3.1小节)大于重构误差阈值θ，则跟踪结果不可靠，跳过此帧以避免引入噪声；否则将该帧所得样本积累到Xtemp中。需要注意的是，当某一帧被跳过时，若临时样本池未收集完毕，则不更新字典。此外，需要说明的是，重构误差阈值θ的选择问题本身就比较复杂。针对此问题，国内外研究人员做了大量研究。笔者根据试验确定θ取值，关于其最优取值问题将在后续研究中予以关注。

2 所提视觉目标跟踪算法

所提跟踪模型基于贝叶斯框架[7]。基于上节所得字典来描述贝叶斯框架中的观察模型，以实现精确的目标跟踪。

对于当前候选目标集Y，需解决如下优化问题：

(17)

其中，Ci表示利用字典Di候选目标集Y所得稀疏编码矩阵，Pi表示对应的误差项，β1为正则化参数。

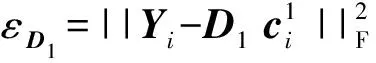
P∝exp(-σεD1/(εD2+δ)) ，

(18)

其中，σ为常数，δ为避免分母为零的约束因子。根据式(18)可估计各候选目标的后验概率。根据贝叶斯推理框架可得目标状态的最优估计，从而实现目标的精确追踪。

3 实验分析

实验硬件环境：处理器为Intel Core(TM) i7-8550U，主频为1.8 GHz，内存为7.88 GB；软件仿真环境为MATLAB R2017b。为验证所提算法的性能，笔者在WU等[11]提出的目标跟踪基准中选取8组测试序列和4种主流跟踪算法进行对比实验。

表1 测试序列及其主要挑战

说明：√表示对应测试序列存在相应的挑战因素。

3.1 参数设置

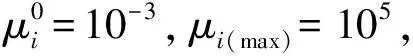
3.2 实验结果分析

图1为5种跟踪方法在8个测试序列上的部分跟踪结果。相应地，其平均中心位置误差和平均跟踪重叠率如表2所示。其中，用加粗字体标识最大平均跟踪重叠率和最小平均中心位置误差，用下划线标识次小值。下面由图1和表1、表2分析所提算法在光照变化、尺度变化、遮挡及背景杂波等挑战下的准确性。

图1 不同算法的部分跟踪结果

(1)光照变化。由表1知，测试序列包括Car1，Car2，Singer1，Faceocc2和Car4。当测试序列发生频繁光照变化时，所提算法仍能稳定跟踪目标，说明所提算法在光照变化下具有较好的鲁棒性，而4种对比算法则丢失了目标或发生严重漂移。图1(e)和图1(h)中，由于TLD算法加入重定位组件，在丢失目标一段时间后重新定位目标，但仍未能精确定位目标。

(2)尺度变化。由表1知，测试序列包括Car1，Dudek，Walking2，Car2，Singer1和Car4。由图1相关测试序列知，当测试序列发生尺度变化时，所提算法能适应尺度变化，具有较好的鲁棒性。然而4种对比算法均丢失了目标或发生漂移。其中，CT算法缺少尺度更新机制，目标外观模型随着目标尺度变化产生冗余或错误，最终导致跟踪失败。由于笔者提出的算法采用非凸极大极小凹加函数惩罚稀疏矩阵和误差矩阵，以获得目标的无偏估计，因而可获得较好的跟踪精度。

(3)遮挡。由表1知，测试序列包括Faceocc1，Dudek，Walking2，Singer1和Faceocc2。由图1相关测试序列可知，当目标发生遮挡时，4种对比算法均发生不同程度漂移或跟踪目标框与真实目标大小不符。特别是在图1(d)中，当目标被另一人遮挡时，4种对比算法均丢失目标。然而，笔者所提算法仍能稳定跟踪目标，具有较高的跟踪精度和鲁棒性，其可归因于所提算法为解决目标遮挡和噪声等问题而加入了误差项。

(4)背景杂波。由表1可知，测试序列包括Car1，Dudek和Car2。由图1相关测试序列知，当目标处于背景杂波且伴随光照或尺度变化的情况下，4种对比算法均发生不同程度漂移或丢失目标。在图1(a)和图1(e)中，目标驶入阴影区域后外观发生较大变化，且和周围背景有较大的相似性，对比算法受到相似目标影响而发生漂移甚至丢失目标。然而，所提算法能稳定锁定目标，具有较高的跟踪精度和鲁棒性，其原因在于所提算法不仅针对目标学习字典，还考虑目标周围的背景信息，利用所得判别字典可有效减轻相似背景干扰。

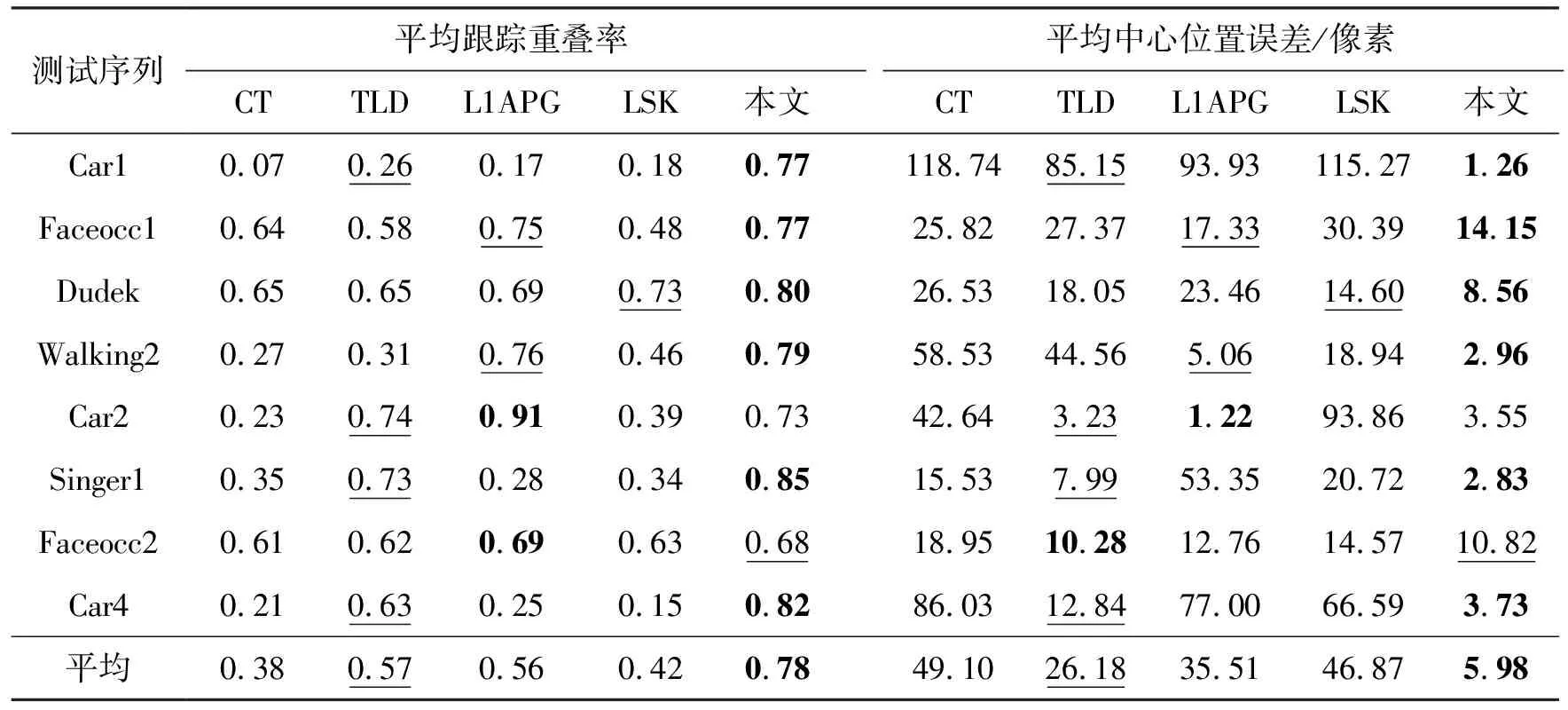
表2 不同跟踪方法的平均跟踪重叠率及平均中心位置误差

由表2可知，所提算法在测试序列Car1，Faceocc1，Dudek，Walking2，Singer1均有较好的表现，其在所有测试序列上的平均跟踪重叠率及平均中心位置误差分别为0.78和5.98。

在目标跟踪问题中，算法运行速度是最重要的性能指标之一。对比5种算法的运行速度，分析所提算法的实时性。表3示出不同跟踪方法在各个测试序列下的平均运行速度(帧/秒)。由表3可知，相较于基于稀疏表示的对比算法，笔者提出的算法及其他对比算法运行速度较高，实时性较好。然而，需要注意的是，虽然其他对比算法比笔者提出的算法运行速度快，但跟踪性能欠佳。

在通常条件下，基于稀疏表示的跟踪算法的计算量与候选粒子数量成正比。基于此，通过合理选择粒子数量，并用复杂度较低的一步局部线性近似方法，可在显著降低算法复杂度的情况下取得较好的跟踪性能。

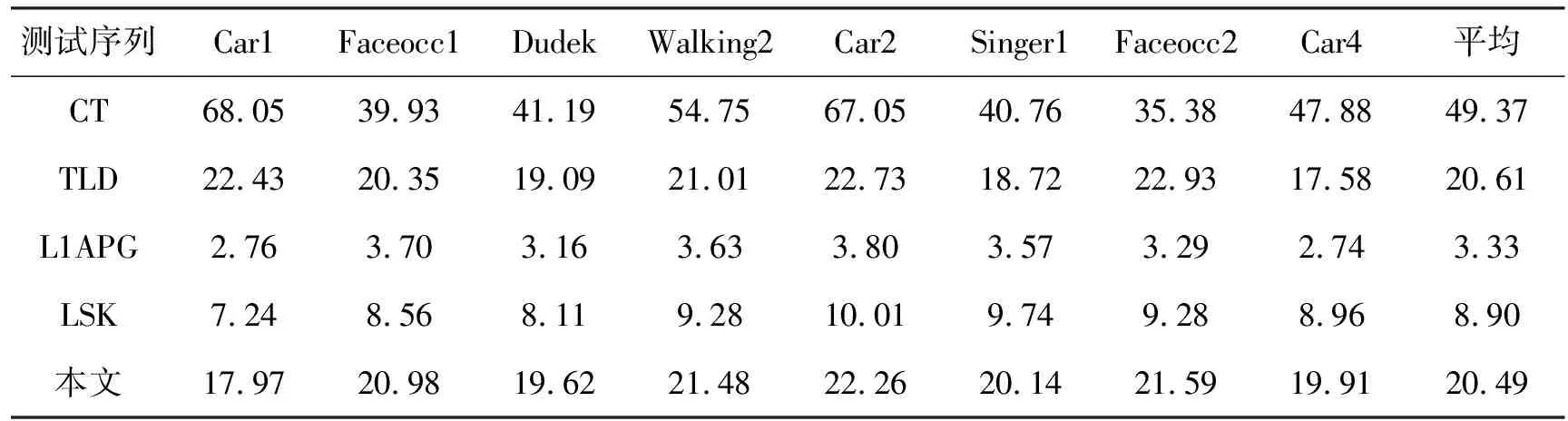
表3 不同跟踪方法在各个测试序列下的平均运行速度 帧/秒

综上所述，与现有的主流跟踪器相比，所提算法具有较好的鲁棒性、精度和时效性。其主要原因归结为：

(1) 所提算法考虑了目标的时空局部相关性，因此不易受背景信息干扰，具有较高的鲁棒性。

(2) 所提算法采用极大极小凹加函数惩罚稀疏和误差矩阵以获得近乎无偏估计，从而获得了更高的跟踪精度。

(3) 所提字典学习模型中字典不一致约束项使目标及背景字典更独立，从而提高了字典的判别能力。

(4) 针对遮挡或噪声等问题，所提算法在字典学习模型中加入误差项以进一步提高算法的鲁棒性和精度。

4 结束语

针对复杂环境下目标跟踪性能显著下降的问题，提出一种视觉跟踪方法。该方法首先根据最近若干帧跟踪结果获取目标样本，并在跟踪结果邻近区域获取背景样本。而后，在字典学习模型中施加不一致约束项使得目标及背景字典更为独立以提高字典的判别能力。同时，针对遮挡或噪声等问题干扰，所提方法利用误差项捕获异常值以改善算法的鲁棒性。此外，该模型使用极大极小凹加函数惩罚稀疏编码矩阵和误差矩阵，以避免l1范数对一些较大变量过度惩罚，从而提高目标跟踪精度。为求解所得非凸判别字典的优化问题，提出基于MM-IALM的求解方法以获得具有较好收敛性的高效求解。最后，根据所获得的最优判别字典构建目标观测模型，并基于贝叶斯推理框架实现目标精确跟踪。仿真结果表明，与现有的主流算法相比，所提方法在光照变化、尺度变化、遮挡及背景杂波等环境下具有较高的跟踪精度及鲁棒性。