上海市典型高层建筑结构基本自振周期测试与回归分析

闫培雷， 孙柏涛

(中国地震局工程力学研究所 中国地震局地震工程与工程震动重点实验室,哈尔滨 150080)

随着经济发展和社会进步，上海市高层建筑从20世纪80年代的121幢已经发展到如今的3万余幢[1]，已成为上海市的主要建筑结构形式之一。上海市一旦遭受破坏性地震或强台风，高层建筑的破坏将造成巨大的经济损失和人员伤亡。高层建筑在风荷载和地震作用下产生振动和变形的大小取决于结构自身动力特性以及外部动力作用的特性。基本自振周期是十分重要的结构动力特性，其可用于反应谱法中估算结构承受的地震作用，计算结构的风压脉动增大系数进而确定结构承受的风荷载，作为控制结构侧移刚度的重要指标并从宏观上判断结构侧移刚度是否合理[2]。

结构基本自振周期可通过理论计算和现场测试两种方法得到。理论计算方法对结构的质量分布、材料实际性能、节点刚度以及施工质量进行了必要简化，计算结果往往大于实际周期，导致采用理论计算周期得到的结构地震作用偏小。现场测试获得的动力特性是建筑物建成后实际性态，其结果准确可靠[3-6]；对比实测周期与理论计算周期，可以验证理论计算中简化方法的合理性；通过对特定结构形式的建筑进行现场测试，归纳总结一定规律，得到其自振周期经验公式，可用于快速估算该结构形式建筑的动力特性及其承受的地震作用[7-10]。

《建筑结构荷载规范》(GB50009—2012)[11]中有关高层建筑的基本自振周期经验公式是基于北京、上海、天津、广州、成都等十几个城市内高度在50 m以下的160 余幢框架结构和80余幢剪力墙结构的实测数据拟合而成的[12]。近年来，上海市新建高层建筑的高度绝大多数都超过50 m，并且高层建筑的结构形式也不局限于框架结构和剪力墙结构，如将文献[12]中的统计规律应用到上海市目前的高层建筑结构设计中，其合理性和精度尚存疑问。本文通过对上海市已建成的9幢典型高层建筑进行现场测试，获得结构动力特性；给出以高宽比为自变量的结构基本自振周期经验公式，供结构设计人员参考使用。本文给出的公式是对我国《建筑结构荷载规范》(GB50009—2012)[11]的补充和完善。

1 结构动力特性测试

1.1 测试结构概况

9幢高层建筑的统计信息如表1所示。结构用途以办公和商业为主；框架-剪力墙结构平面内两个主轴方向的尺寸相差较大，多呈“板式”，框架-核心筒结构平面内两个主轴方向的尺寸接近，多呈“塔式”；结构刚度沿竖向变化基本均匀。

1.2 现场测试方案

1.2.1 测试方法

采用环境激励法(亦称脉动法)对结构进行动力特性测试。环境激励法利用结构对自然环境下微弱干扰的脉动响应来确定其动力特性。环境激励法不采用外部激振设备，对结构无损伤，不影响结构正常使用，在自然环境条件下即可测定结构动力特性。

1.2.2 测试方案

在现场测试前，搜集结构施工图并查找结构高度、长度和宽度等信息，依据结构平面图计算确定结构平面刚度中心和质量中心。

表1 建筑物的基本信息

每栋结构均设置两个测试点，分别位于顶层刚度中心和总高度一半处楼层的刚度中心；每个测点分别测试3次，每次测试的振动响应(速度)数据包含1条水平纵向数据和1条水平横向数据。

1.2.3 仪器及布置

仪器采用中国地震局工程力学研究所研发的G01NET-2通用数据采集器和941-B超低频测振仪。G01NET-2是多通道数据同步高速采集仪(如图1)，主要应用于结构测试中振动信号的采集、分析及处理，其性能在国内处于先进水平。941-B型超低频测振仪是一种用于超低频或低频振动测量的多功能仪器(如图2)，主要用于地面和结构物的脉动测量，仪器具有体积小、重量轻、使用方便、分辨率高、动态范围大等特点。

图1 G01NET-2通用数据采集器

941-B型超低频测振仪的布置原则如下：

(1) 在结构平面内，941-B超低频测振仪尽可能安放在结构的刚度中心处，并按结构水平纵横双向布置，保证测振仪接收到的信号突出平动信号，扭转振动信号尽可能小；

图2 941-B超低频测振仪

(2) 在结构的竖向上，由于结构速度幅值随层数的增加而增大，因而在结构顶层及结构总高度一半处的楼层布置布置941-B超低频测振仪，即可获得可靠准确的数据，不必层层布置测振仪。

1.2.4 数据采集

现场测试时，单次数据采样时间为5 min，采样频率为50 Hz；环境激励包含的频谱非常丰富，可近似为有限带宽白噪声，在保证单次测试时间长度一定的前提下，即可用结构脉动响应的单个样本函数来描述随机过程的所有特征，并明显反映出结构的动力特性。

2 测试数据及处理

2.1 数据处理

将采集得到速度时程数据经过快速傅里叶变换(FFT)得到结构脉动响应功率谱[13-14]，采用峰值法识别结构的基本自振周期，而后将6组结果取平均值，最终获得结构在水平纵横两个方向上的基本自振周期，9幢高层建筑的水平纵横两个方向的基本自振周期结果如表2所示。以上海市黄浦区的来福士广场3号楼为例(如图3和图4)，现场测试数据如图5，数据处理结果如图6。

图3 来福士广场3号楼

图4 结构顶层动力性能测试

图5 水平横向速度时程数据

图6 水平横向功率谱

2.2 测试结果

表2 结构测试结果汇总

3 框架-剪力墙结构的基本自振周期经验公式

《建筑结构荷载规范》(GB50009—2012)[11]中给出的钢筋混凝土框架结构和框架-剪力墙结构的基本自振周期经验公式如下所示：

(1)

依据式(1)对测试的5幢框架-剪力墙结构的基本自振周期进行了计算，并与实测结果进行了对比，结果如表3所示，表3中的误差定义为：

(2)

表3 测试结构自振周期与经验公式对比

Tab.3 Comparison between fundamental vibration period acquired and that calculated by empirical formula

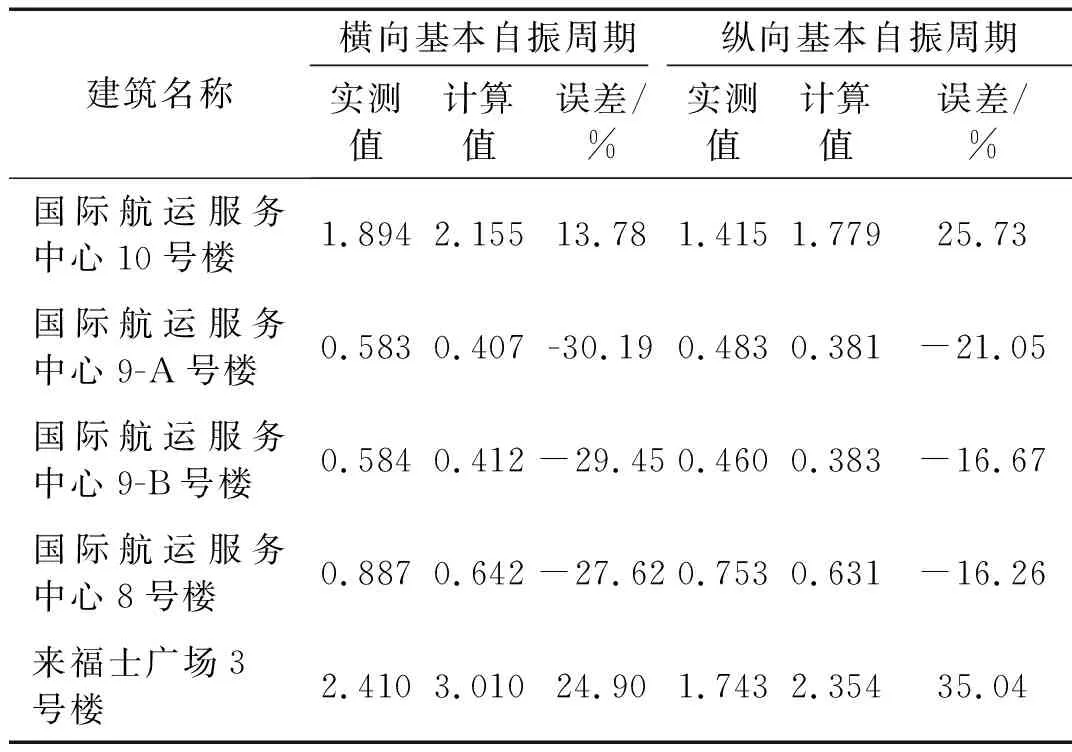
建筑名称横向基本自振周期纵向基本自振周期实测值计算值误差/%实测值计算值误差/%国际航运服务中心10号楼1.894 2.155 13.78 1.415 1.779 25.73 国际航运服务中心9-A号楼0.583 0.407 -30.19 0.483 0.381 -21.05 国际航运服务中心9-B号楼0.584 0.412 -29.45 0.460 0.383 -16.67 国际航运服务中心8号楼0.887 0.642 -27.62 0.753 0.631 -16.26 来福士广场3号楼2.410 3.010 24.90 1.743 2.354 35.04

从表3看出，实测值与式(1)的计算值存在较大误差，其中国际航运服务中心10号楼和来福士广场3号楼为办公楼且高度均超过100 m，为保证结构具有足够侧向刚度和使用功能，平面内布置了较多的钢筋混凝土剪力墙和隔墙，导致结构实测值较计算值小，误差为正；其它3幢结构平面内仅布置了少量的钢筋混凝土剪力墙，且较为空旷，结构整体侧向刚度较弱，导致结构实测值较计算值大，误差为负。因此，判断式(1)对高度超过50 m的框架-剪力墙结构不适用。

环境激励法实测的基本自振周期是结构在微小变形下的性能参数；抗震设计所需的是结构在地震中发生足够强的振动但不进入非线性反应时的基本自振周期，该值大于环境激励法实测的基本自振周期。因此，需将环境激励法实测的基本自振周期乘以修正系数。针对钢筋混凝土框架结构和框架-剪力墙结构，依据王广军等[15]研究，修正系数取1.15。

参考式(1)的形式，同时考虑测试结构平面形状以“板式”为主，对结构基本自振周期和高宽比采用SPSS22.0统计分析软件在水平纵横两个方向分别进行回归分析，其结果如图7和图8所示。

图7 水平横向上的基本自振周期经验公式

Fig.7 Empirical formula of fundamental vibration period in the horizontal direction

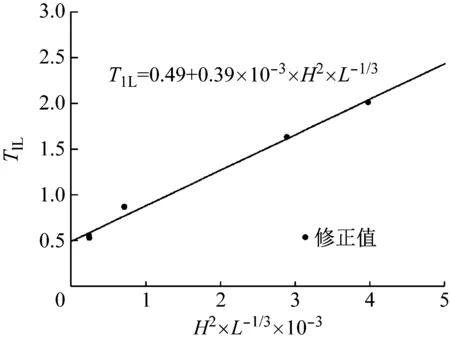
图8 水平纵向上的基本自振周期经验公式

Fig.8 Empirical formula of fundamental vibration period in the longitudinal direction

(3)

式中：T1h为结构水平横向基本自振周期；H为结构高度；B为结构宽度。

该方程的归回分析的决定系数R2=0.994。

(4)

式中：T1l为结构水平纵向基本自振周期；L为结构长度。

该方程的归回分析的决定系数R2=0.992。

拟合结果显示，所得公式的决定系数非常高，说明高层钢筋混凝土框架-剪力墙结构的基本周期与结构高宽比有显著的关系，基本自振周期随着高度的增加而增大。

选择文献[16]中的钢筋混凝土框架-剪力墙结构用于验证式(3)和式(4)的可靠性。该结构的高度为49.5 m，宽度为22.7 m，长度为91.6 m。从表4可以看出,公式误差率控制在17%之内，该精度在结构初始设计阶段能够满足快速估算结构承受水平地震作用和风荷载的需求。

表4 测试结构自振周期与式(3)、(4)对比

Tab.4 Comparison between fundamental vibration period acquired and that calculated by formula (3) and (4)

横向纵向实测值/s式(3)值/s误差/%实测值/s式(4)值/s误差/%0.7250.63712.10.6040.70216.2

4 框架-核心筒结构的基本自振周期经验公式

针对框架-核心筒结构，依据方鄂华等[17]研究，修正系数取1.20。参考式(1)的形式，考虑测试结构平面形状以“塔式”为主且两个主轴方向实测数据存在显著差异，对结构基本自振周期和高宽比采用SPSS22.0统计分析软件在水平纵横两个方向分别进行回归分析，其结果如图9和图10所示。

图9 水平横向上的基本自振周期经验公式

Fig.9 Empirical formula of fundamental vibration period in the horizontal direction

图10 水平纵向上的基本自振周期经验公式

Fig.10 Empirical formula of fundamental vibration period in the longitudinal direction

(5)

该方程的归回分析的决定系数R2=0.956。

(6)

该方程的归回分析的决定系数R2=0.915。

拟合结果显示，所得公式的决定系数非常高，说明高层框架-核心筒结构的基本周期与结构高宽比有显著的关系，基本自振周期随着高度的增加而增大。

选择文献[18]中的钢筋混凝土框架-核心筒结构用于验证式(5)和式(6)的可靠性。该结构的高度为141 m，宽度为41.5 m，长度为44 m。从表5可以看出,公式误差率控制在30%之内，该精度在结构初始设计阶段能够满足快速估算结构承受水平地震作用和风荷载的需求。

表5 测试结构自振周期与式(5)、(6)对比

Tab.5 Comparison between fundamental vibration period acquired and that calculated by formula (5) and (6)

横向纵向实测值/s式(3)值/s误差/%实测值/s式(4)值/s误差/%2.4493.07725.62.0432.62428.4

5 结 论

基于上海市9幢典型高层建筑的动力性能现场测试数据，识别了结构在水平纵横两个方向上的基本自振周期并进行了统计分析，得到了结构在水平纵横两个方向上的基于结构高宽比的基本自振周期经验公式。主要结论如下：

(1) 给出了高度在30～130 m之间的结构在水平纵横两个方向上基本自振周期经验公式，对实测结构的误差为17%之内，该公式是对现行规范中结构基本自振周期经验公式相关规定的补充和完善；

(2) 首次给出了高度在90～190 m之间高层框架-核心筒结构在水平纵横两个方向上基本自振周期经验公式，对实测结构的误差为30%之内；

(3) 在高层建筑的初始设计阶段，可以利用本文拟合的公式，基于结构的总高度、长度和宽度，估算结构的基本自振周期，进而利用反应谱法快速估算结构承受的地震作用以及确定风荷载，最终基于上述分析控制整体结构设计。