风速时间序列模拟的模型有效性验证及代表性风场实例分析

马 赛， 褚福磊

(清华大学 机械工程系， 北京 100084)

风速时间序列分析对于风力资源的评估以及风力发电机组的设计都具有重要的意义。首先，能量密度曲线可以给出一地区的主要风能密度区间，显示出其风力资源水平。为了获得较高的风力转化效率以及并网稳定性，风力发电机组的设计应以符合该地区主要风能密度区的特征为首要目标。而在风力发电机组的设计阶段，为了使叶片以及机械结构(行星齿轮、轴承等)满足设计要求，需要对其在复杂激励环境下的结构响应进行合理地模拟。风速时间序列的模拟就是环境激励模拟的一个重要组成部分，在该模拟过程中，功率谱密度模型的选择对于模拟结果具有直接的影响，合理的模型选择可以产生较为逼真的风速激励形式，进而有效地实现结构设计与改进。

近年来随着可再生能源产业的不断发展，国内外工程技术人员对风力资源评估以及风速时间序列模拟等问题开展了广泛的研究。考虑到基于气象观测数据分析方法的不足[1]，基于风场数据能量密度曲线的风资源评估方法受到了研究人员的关注[2-4]。现有的风场数据分析结果大多面向局部地区风场，缺少大跨度区域风场资源分析结果的对比[5]，因此难以形成对基于中尺度天气预报模式(Weather Research Forecasting，WRF)的风资源评估方法的有力补充与实际验证。

对于风速时间序列模拟这一问题，我国国家标准中仅对风速谱模型的选择给出了建议，但缺少对其建议的实例验证。国内研究人员在对国内风场的风速时间序列模拟问题展开研究时，一般采用首先假定风速谱模型，然后依据模型生成模拟风速时间序列的方式[6-9]。该方式的局限性在于：其仅适用于模拟已验证所选用谱模型适用性的风场。然而对于具体风场，考虑到其地理、大气等因素的影响，具体风速模拟的谱模型选择依据尚需进一步明确。文献[10-12]中虽给出了模型选择结论，但研究仅对某一特定区域风场进行了实例验证，模型的跨区域通用性有待确认。因此针对不同区域的具体风场而言，如何选择风速谱模型对其风速时间序列进行模拟具有重要的工程意义。本文中针对这一实际问题，立足于全国范围内代表性风场的全年监测数据，给出了风场时间序列模拟时的模型选择一般准则，并对该准则进行了我国境内跨区域风场的实例验证与分析。

本文探讨的是在风力发电机组的前期设计过程中，能量密度曲线与功率谱密度模型对于风力发电机组选型与设计所具有的意义。通过计算与对比能量密度曲线，可以明显的观察到目标风场所具有的风力特征；而通过对比功率谱模型与风场实测数据功率谱之间的关系，可以评估经典功率谱模型在模拟过程中的有效性，给出模型的最佳选择。

1 风场的能量密度函数

能量密度定义为每平方米内的风能水平，单位是W/m2。对于具体风场的能量密度函数是通过概率密度函数的形式给出的，风能密度的概率密度水平给出了该风能密度取值的持续时间。良好的风力资源一般同时具有较高的风能密度水平和对应的概率密度水平。式(1)给出了能量密度函数的计算方法：其中x表示风速，ρ为当地空气密度。从式(1)中可见：风能密度函数与风速时间序列的取值呈单调递增的幂指数关系。

(1)

1.1 含参数概率密度估计

考虑到风能密度曲线与风速时间序列取值的关系，为了得到目标风场的能量密度曲线，首先需要对风速时间序列的概率密度函数进行估计，在该概率密度函数的基础上，可以通过一定的数学变换得到能量密度函数的概率密度曲线。这里给出了几种可靠的风速时间序列概率密度函数[13-16]：

1) Weibull分布：

(2)

2) Rayleigh分布：

(3)

3) Gamma分布：

(4)

4) Lognormal分布：

(5)

式(2)～(5)给出的几种概率分布是经典的风速数据分布模型。对于任意的风速时间序列，一般首先假设其服从其中一种概率分布模型，将实测数据对分布参数进行拟合，然后得到较为准确的风速概率分布曲线。

1.2 自变量函数的概率密度函数-变量代换

从式(1)可以看到：风速的能量密度函数与风速呈3次幂单调指数关系，因此可以通过变量函数法计算能量密度的概率密度函数。变量函数法表达式如式(6)所示，其中P(·)表示能量密度函数。

(6)

由式(1)中的风速与能量密度函数关系与式(6)的概率密度函数变换关系就可以计算得到风场能量密度的概率密度函数。

1.3 概率密度函数检验与确认

为了得到风速时间序列的准确概率密度函数，文中采用了最大似然估计法[17](Maximum Likelihood Estimation)与 Kolmogorov-Smirnov检验对各风场数据的概率密度参数进行了估计，并对估计结果进行了统计模型的确认，确定了各风场的有效建模方法，具体结果如表1所示。

如表1所示，除4号风场外，其余1，2，3，5号风场均采用非参数法估计其概率密度函数。因为经过KS检验后发现4号风场服从置信度为95%的Gamma分布。而另外几处风场没有通过KS检验，因此采用了非参数法估计其概率密度函数。

表1 风场编号与相应建模方法

1.4 非参数概率密度估计-核密度估计

核密度估计方法一般用于难以确定其概率密度模型的概率密度估计问题。文中对于未通过KS检验的4处风场(1，2，3，5号)采用了该方法建立概率密度模型。式(7)为核密度估计方法的表达式：

(7)

式中:n表示待拟合的数据点数，h为拟合窗宽度，其取值按照文献[18]确定，K(·)为拟合函数形式。

2 时间序列的功率谱描述

相关函数是在时间域内反映两信号相关程度的指标。在风速时间序列评估体系中，为了评价其相关性时间尺度，需要计算自相关函数，然后通过频域变换得到其功率谱描述。

自相关函数的表达式为：

(8)

式中:f(t)为风速时间序列；当R=0时，表示x(t)和x(t+τ)之间在各时间段上均互不相关；当R=1时，表示x(t)和x(t+τ)之间在各时间段上完全相关。

式(9)、(10)中的Gxx(f)、Gyy(f)分别为输入信号x(f)，输出信号y(f)的单边自功率谱；Gxy(f)为x(f)与y(f)的单边互功率谱：

(9)

(10)

功率谱函数反映了频域上时间序列各时刻之间的相关性，如果功率谱函数的取值主要集中在低频，说明原始时间序列具有长相关性；如果功率谱函数的取值分布在频域上较平坦，则说明原始时间序列随机性较强。

3 风速时间序列模拟方法

为了合理地模拟特定时间序列，首先需要提取其稳定的特征用于重构，而对于风速载荷这样一类随机性较强的时间序列，其稳定的特征包括功率谱函数与概率分布函数两类。由于概率密度函数的估计结果时常产生难以避免的误差，因此工程上一般选用结合功率密度函数的Monte Carlo方法生成风速载荷时间序列[19]。其中常用的风速载荷模拟方法包括：①滤波变换法以及②谐波叠加法，两种方法在应用之前都需要恰当地选取目标时间序列的功率谱模型。

3.1 滤波变换法

滤波变换法的思想是：将白噪声时间序列与一个滤波器或滤波器组做卷积运算，可以得到具有目标特征的风速时间序列。该方法中所采用的滤波器组，其系数是由功率谱模型经过傅里叶反变换得到的，因此可以保证所生成的目标序列与选用的功率谱模型具有相同的统计参数。

图1中给出了生成一维风速时间序列的模拟流程，其中的HL(t)、HH(t)两个变量分别代表了风速时间序列的低频部分与高频部分。

图1 滤波变换法流程图

采用这一类方法生成风速时间序列所选用的模型包括：Dryden谱，von Karman谱[20]，Kaimal谱[21]等。本文中将对其中应用较为广泛的von Karman谱以及Kaimal谱进行对比分析。

3.2 谐波叠加法

谐波叠加法是在目标频段上随机选取频率点，将这些频率点服从均匀分布的三角函数进行叠加以生成目标风速时间序列。该方法属于一种门特卡罗模拟，通过提高叠加频率点的数量可以对随机或长相关时间序列进行有效的逼近。

图2 谐波叠加法流程图

由图2所示，生成的各阶谐波叠加后的结果就是目标风速时间序列的模拟结果：

(11)

式中:ω表示随机选择的频率点，θ为对应的相位。利用该方法将50个以上的谐波函数叠加就可以对风速时间序列进行较准确的模拟。但是与滤波变换法相同的一点是，该方法也依赖于所选择的时间序列功率谱模型。

4 经典功率谱模型

对于风速时间序列而言，经典的功率谱模型包括四种。在国际上，von Karman模型与Kaimal模型较广泛地应用于风速时间序列模拟以及风场评估；Davenport模型[22]与Mann模型[23]在国内应用较多。以下依次对各模型予以介绍说明。

4.1 von Karman模型

von Karman模型的表达式如式(12)所示，其中参数f表示频率，σ表示风速标准差，L表示湍流积分尺度，Vhub表示轮毂高度处的平均风速。

(12)

von Karman模型属于较早期提出的功率谱模型，相对于后期发展的模型而言，其更适用于自由流动场的风速时间序列的模拟。当风场地表的构型存在剧烈变化以及各风力发电机组具有尾迹干扰效应时，该模型的模拟能力存在一定的缺陷。另外，不同方向上的湍流积分尺度L也具有较大的差异，因此在应用该模型时应该对不同流动方向分别予以考察。

4.2 Kaimal模型

式(13)为Kaimal模型的表达式，其中的各参数与von Karman模型定义相同。

(13)

Kaimal模型相对于von Karman模型的改进之处在于假设不同方向上的风速时间序列是独立的，因此在模拟三维风速流场时具有更高的精度。

4.3 Davenport模型

Davenport模型相对于前两种模型的不同之处在于假设湍流积分尺度沿高度不变为常数1 200，并且该模型为各高度下风速功率谱平均值表达式。

(14)

(15)

(16)

式中:参数V10表示10 m高度处的平均风速，K表示地面粗糙度。该模型在早期的风速模拟过程中应用广泛，但粗糙度系数K的取值缺少明确的解析表达式，因此会在风速模拟结果中引入较大的误差，降低了该模型的可用性。

4.4 Mann模型

Mann模型[23]为一种均匀切变湍流模型，其功率谱表达式如式(17)所示：

(17)

σ1=Iref(0.75Vhub+5.6)

(18)

式中:∧1为高度大于70的取值42。Iref为风速在15 m处的湍流期望值，本文中取0.14。Mann模型相对于von Karman模型引入了切变变性参数，使得自身在三个方向上的方差可以随该参数变化[23]。

值得注意的一点是：对于垂直于迎风面的风速时间序列，各模型的不同之处主要来自于表达式中含频率项的指数，该指数决定了功率谱幅值随频率增加的衰减速率。

5 实测风速数据分析

本文所分析的风速数据来源于中国境内的五座风场，其位置分别位于宁夏(代表中西部地区)、黑龙江(代表北部地区)、安徽(代表中东部地区)、甘肃(代表中西部地区)，广东(代表南部地区)等五个省份，具体编号如表1所示。

5.1 风速数据描述

风速时间序列均为表1中五座风场的近五年内某年份的全年风速数据，考虑到气候变化的周期性，风场在各年份间的风力资源较为相似，因此以全年风速数据作为分析对象是合理的。其采集间隔为10 min，测风塔高度为70 m。在分析数据时选择切入风速(风力发电机组启动风速)与切出风速(风力发电机组最高工作风速)分别为3 m/s和20 m/s。

5.2 能量谱对比分析

任意风场能量密度的表达式如式(1)所示，本节中采用本文第一节内容中的含参数概率密度估计方法、非参数概率密度估计方法以及变量变换法分别计算了五处代表性风场的能量密度曲线[25-29]，具体结果如图3所示。图1中的横坐标表示能量密度，单位为W/m2，纵坐标表示概率密度的取值。从该图中可以发现：我国东南沿海地区风场的风力资源最为丰富(5号风场)，其有效风能密度区(200～400 W/m2)的持续时间最长(概率密度取值最高)；北部地区(2号风场)风场的风力资源也较为丰富，且在高风能密度区(>500 W/m2)相对于其他地区具有一定优势；对于主要风力资源集中在低风能密度区(<200 W/m2)的部分地区风场(3号风场)，在风力发电设备选型时应该有针对性的进行结构设计，以期获得较高的转化效率以及并网电力的良好稳定性。

图3 各地区代表性风场的能量密度曲线

5.3 功率谱对比分析

本节中采用前文所述的功率谱模型对五处代表性风场的全年风速时间序列进行了分析与对比。图4～图7给出了表1中五处风场全年风速时间序列的功率谱曲线以及对应的von Karman模型、Kaimal模型、Davenport模型、Mann模型曲线。

图4～图7中各模型均对功率谱函数进行了归一化。从各图中可以看出：相对于实测数据功率谱曲线，Kaimal模型、von Karman模型以及Davenport模型在整个频段上的功率幅值均存在着较大的差别，这一差异会导致所生成的模拟风速时间序列与实际载荷在幅值上的显著差异。

Mann模型相对于另外三种模型较好地模拟了五座风场实际风速时间序列的功率谱。其主要的优势在于功率谱函数随频率增加而衰减的趋势与实测数据保持一致。其中，1、2、4号三座风场数据吻合度高，而3、5号两座风场数据吻合度存在一定的差距，但相对于其它模型而言，该结果仍是可以接受的。

Mann模型的理论基础是湍流模拟中的快速畸变理论，由于假设在高度区间内风速轮廓线保持线性变化，因此使得Navier-Stokes可以被线性化并用于描述湍流的空间二阶结构。在N-S方程求解过程中考虑到风速输送动量以及湍流尺度等因素忽略了非线性项以及粘性项。Mann模型相对于其他功率谱模型的主要区别在于在模型中考虑了“涡寿命时间”，因此在模拟功率谱时具有较为合理的频率衰减系数(功率谱曲线的斜率)，进而可以更好地描述实际风速的功率谱。采用Mann模型在设计阶段模拟风速时间序列可以更准确地给出结构设计需求，提高设计精度，因此对于国内风场的风速时间序列模拟问题是一个较为合理的选择。

另外，从图4～图8中的功率谱曲线可以发现：1号、5号风场具有12小时的周期波动成分，而3号、4号、5号风场具有24小时周期波动的成分，体现出风力资源的短时波动性质，在对风电资源进行调度时应予以考虑。

值得注意的一点是：所采用的四种模型对于5处风场功率谱在低频部分的拟合程度仍存在精度不足的问题，文献[30]对这一问题进行了深入细致的研究和理论推导，对Mann模型的两个重要参数进行了修正，可以有效提高风功率谱低频范围的模拟精度。

从实测风速数据的功率谱曲线以及四种功率谱模型可以看到，风速时间序列属于典型的1/f过程，其功率谱函数的取值随着频率的增加而衰减。不同的1/f过程的差异在于功率谱函数衰减的速率或指数，文中与风场数据衰减较为一致的Mann模型，其衰减速率较高，这一类过程具有长程相关的特征；而其他模型的衰减速率较低，功率谱曲线在频率域上分布较为平坦，因此具有短时相关或者随机过程的特征。

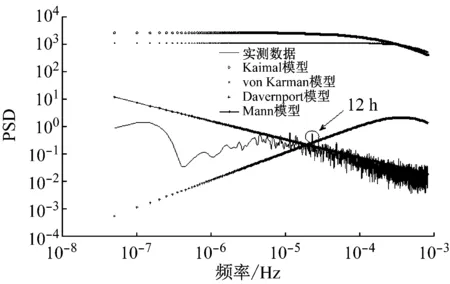
图4 1号风场功率谱曲线与四种模型对比

图5 2号风场功率谱曲线与四种模型对比

图6 3号风场功率谱曲线与四种模型对比

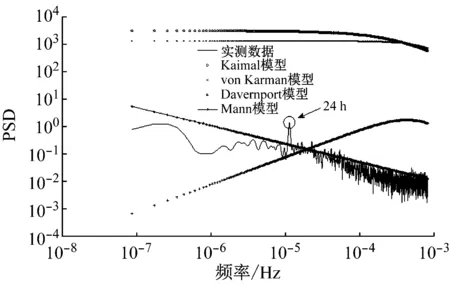
图7 4号风场功率谱曲线与四种模型对比

图8 5号风场功率谱曲线与四种模型对比

6 结 论

本文以国内各地区五处代表性风场的风速时间序列为对象进行了能量谱与功率谱计算，对各风场的能量密度曲线以及四种经典的功率谱模型进行了对比与分析，得出了如下几点结论：

(1) 从各地区代表性风场的能量密度曲线对比结果来看，我国东南沿海以及北部地区风场的风力资源较丰富，而各地区的风场在不同的能量密度区间具有各自的优势。

(2) 采用滤波变换法与谐波合成法对风速时间序列进行模拟时，功率谱模型的选择对模拟结果的精确程度具有直接的影响，应选择与目标风场实测功率谱较为匹配的模型开展风速模拟。

(3) 国内五座风场风速的功率谱曲线与Mann模型吻合较好，而与其他模型存在着较明显的差异，因此应该在模拟风速时间序列时选择Mann模型。

(4) 国内风场风速时间序列在时域上具有长程相关的特征，可以针对这一特点对风速载荷的快速模拟以及预测方法进行进一步的研究。