一类电磁式薄膜振动能量采集器动力学建模与非线性分析
王志霞, 王 炜, 张琪昌
(1.天津大学 机械工程学院,天津 300350;2.天津市非线性动力学与控制重点实验室,天津 300350)
能量采集技术能够将日常生活中广泛存在的机械能、光能和热能加以收集转化形成可供利用的电能并为微传感器供电[1]。作为环境能量的主要形式之一,机械振动不受温度、尺度、地域等条件制约,具备成为可靠电源的基本要素。根据其工作原理的差异,目前的振动能量采集器可分为电磁式、压电式、电容式和磁致伸缩式[2-8],其中电磁式振动能量采集器(Electromagnetic Vibration Energy Harvester,EMH)具有低频性好、输出电流较大、无需驱动电源等优点,拥有广泛的应用前景[9-10]。
EMH由永磁体、感应线圈绕组和弹性元件组成。在外界激励作用下,永磁体与线圈之间产生相对运动,导致穿过线圈的磁通量发生变化,从而产生感应电动势[11]。在EMH的发展过程中,虽然不同学者秉承的设计理念、研究重心不尽相同,但其关心的目标始终是增加带宽、提高输出功率[12]。其间涌现出的比较有代表性的工作包括:Williams等[13]利用薄膜振动原理,设计了最初的EMH模型,在实现了装置小型化的同时,还基于线性振子的思想对结构进行了优化,强调了空气阻尼对于薄膜振子输出功率的影响,但并未对相关问题做进一步的深入分析,整体输出功率只有0.3 μW。考虑到自然环境中激励形势比较复杂,Khan等[14]设计了适合于小幅正弦周期激励和窄带随机激励的薄膜振子模型,采用数值方法对其中的非线性现象进行了分析。同时,Khan等[15-16]还首创了电磁式噪声能量采集器,将基础振动转化为声压变化引发薄膜振动,进而扩展了EMH的应用范围。虽然薄膜类型EMH的研究起步较早并且具备结构小型化的发展空间,但由于振动过程中易受空气阻尼影响且输出功率有限,因此目前应用更为广泛的是悬臂梁结构的EMH。基于线性振子理论,Ei-Hami等[17]较早开展了此类模型的研究,完成了理论模型分析、有限元结构优化在内的工作。Glynne-Jones等[18]通过增加永磁体数量的方式强化了线圈周围的磁场强度,与常规的悬臂梁振子相比,不仅结构更为小巧而且具备更优的低频性能(在52 Hz的激励下,其输出功率为46 μW)。但是悬臂梁线性EMH的工作频带有限,激励频率远离其固有频率时,输出电压将骤然下降[19]。
随着相关工作的不断深入,研究人员意识到了非线性手段能够在扩大带宽、改善输出效果方面发挥积极的作用,并广泛开展了非线性EMH的研究。Soliman等[20-21]利用限位器产生分段非线性效应以增加悬臂梁振子带宽,并且采用谐波平衡法研究了振子的振动特性。Kluger等[22]讨论了曲面非线性刚度对于振子带宽的影响,指出该方式有助于增加结构的工作寿命,改善振子在日常复杂激励环境中的能量采集表现。Lee等[23]使用磁力弹簧结构拓宽样机带宽,增加了线圈绕组的磁通量,提高了样机的能量转化效率,使结构在0.2 g加速度下带宽为9.5~11.5 Hz,输出功率由0.68 mW(线性能量采集器)提高到2.27 mW。Barton等[24]较早提出了双稳态振子模型,振动过程中悬臂梁末端磁铁受右端定磁铁磁力作用,出现了在两个平衡点附近振动的现象,并证明了该现象的存在能够有效地扩大振子的带宽,非常适合于日常的工作环境。
通过上述分析可以发现,虽然国内外研究者广泛讨论了柔性薄膜与磁力弹簧对于振子带宽的影响,但是在已有器件中,薄膜结构EMH依旧以单稳态运动为主,多稳态振动形式的应用及其相关理论背景、设计优化思路仍有待进一步完善。同时,考虑到薄膜振子的结构优势(如:成本低廉、低频性能好、兼容能力强等),如何充分发挥这一优势、释放其结构潜能,就成为EMH研究中亟需解决的科学问题。
有鉴于此,本文将柔性薄膜和磁力弹簧相结合,提出一种了能感应低频小幅振动且具备较宽工作频带的双稳态电磁式振动能量采集器(Bistable Electromagnetic Vibration Energy Harvester,BEMH)。首先,介绍了结构装置示意图及其工作原理;其次,考虑不同的非线性要素建立了薄膜大变形模型,并将其引入样机动力学控制方程;再有,利用数值仿真及实验手段获得了结构的主要物理参数,并从数值及实验两方面对BEMH振子的运动特性进行了深入的分析,验证了本模型相对于传统单稳态薄膜结构在能量转化效率、工作带宽方面的优势。
1 结构装置及振动控制方程
1.1 结构装置及工作原理
图1为设计的双稳态电磁式振动能量采集器的结构示意图。BEMH主要包括薄膜、中间质量块、铁芯线圈绕组、腔体壁。Ø80×0.35 mm3乳胶薄膜通过环氧树脂固结于夹片;中心质量块为NdFeB磁铁(Ø18×2 mm3)吸附于乳胶薄膜两侧;Ø40×20×5 mm3铁芯线圈绕组通过环氧树脂固定于样机的上下端盖,其中线圈绕组由高导电的漆包线组成(N=100圈);样机腔体壁采用非导磁铝材料,防止磁通量泄露导致输出能量的降低。旋转上下端盖可调节磁力弹簧刚度,同时可改变通过线圈绕组的磁通量。上下端盖具有可调扇形阻尼孔,后续可研究空气阻尼对能量输出的影响。
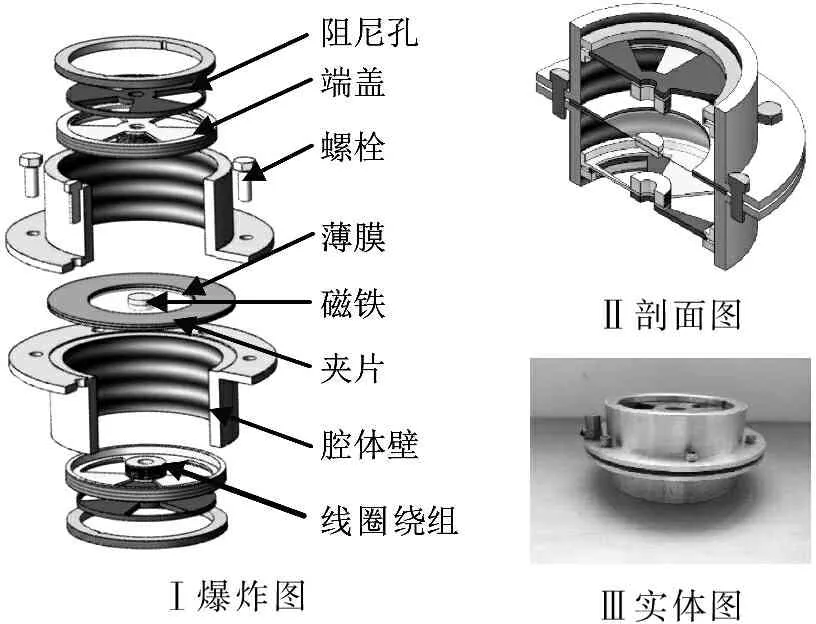
Ⅰ爆炸图Ⅱ剖面图Ⅲ实体图
图1 BEMH结构示意图
Fig.1 The structure of BEMH
样机工作原理:外界振动垂直作用于薄膜平面方向,引发薄膜振动并带动永磁体在采集器腔体内做上下往复运动,使得上下端盖缠绕的导电线圈发生磁通量变化产生感应电动势。若采用压电薄膜替换本模型中的乳胶薄膜,则此能量采集器即变为混合式振动能量采集器。
1.2 薄膜弹性组件模型
此处分析具有中间质量块薄膜振子大变形状态下的强非线性回复力。图2为薄膜弹性元件的简化模型,取元件静平位置O为坐标原点,考虑半径为r处的挠度ω(r,t),由虚功原理可得系统振动控制方程:
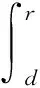
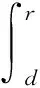
(1)
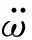
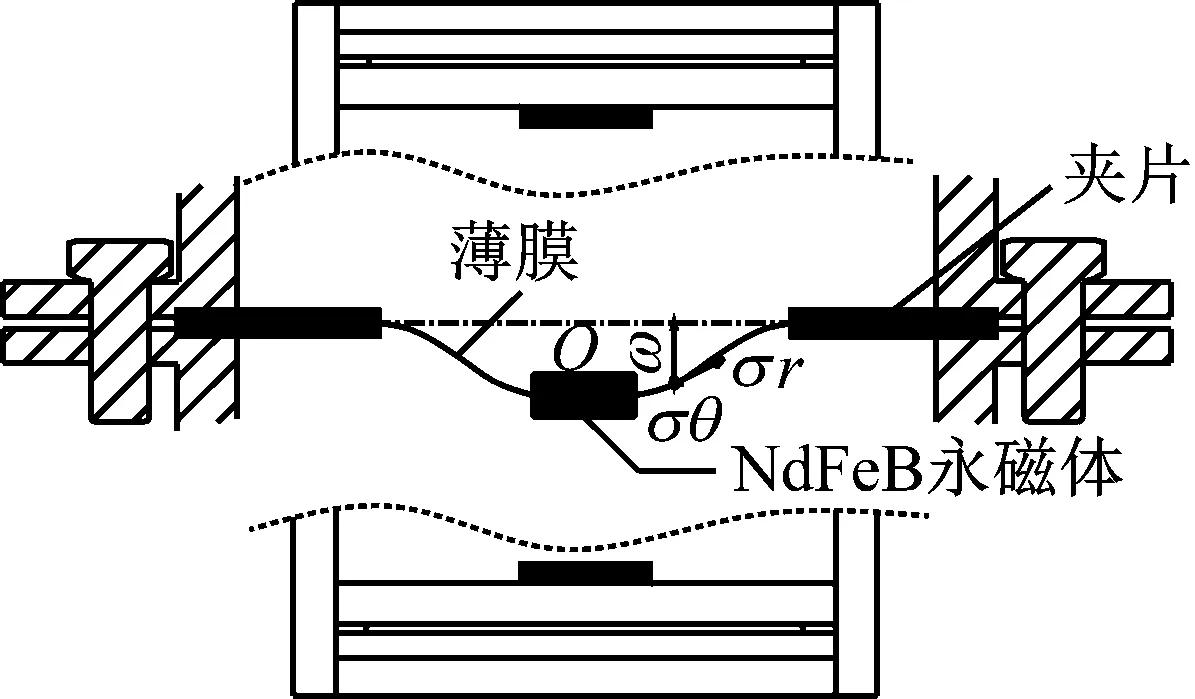
图2 薄膜弹性组件模型
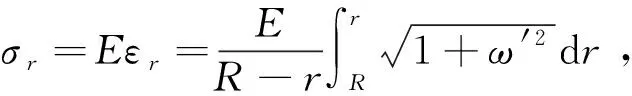
ωr=R=0
(2)
(3)
(4)
式中:R为薄膜半径;E为薄膜弹性模量;ω″为薄膜挠度对径向位置的二阶导数。若仅研究薄膜静态位移,则式(3)和式(4)分别变为:
(5)
(6)
考虑薄膜静挠度:
ω(r)=ω0(r)+εω1(r)+ε2ω2(r)
(7)
联立式(2),(5)~(7),得薄膜回复力表达式为:
Fr(ω,r)=
(8)
1.3 系统动力学模型
取系统静平衡位置O为坐标原点,x轴铅直向下为正方向,由牛顿定律得:
Mg+Fm=Fr
(9)
当薄膜偏离静平位置x时,由达朗贝尔原理得:
(10)
联立式(9)和(10),得系统运动微分方程:
(11)
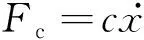
利用无量纲变换:
(12)
式(11)简化为如下的二阶常微分方程:
(13)
其中:
1.3.1 系统静态稳定性分析
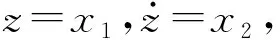
(14)
由势能函数图3所示(其中,xi0为系统的静平衡位置坐标,i=1,2,3):
① 1-μ>0,a=b=0,结构为线性系统,只存在中心点(0,0)。
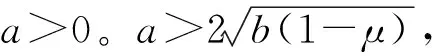
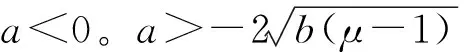
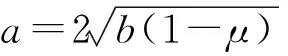
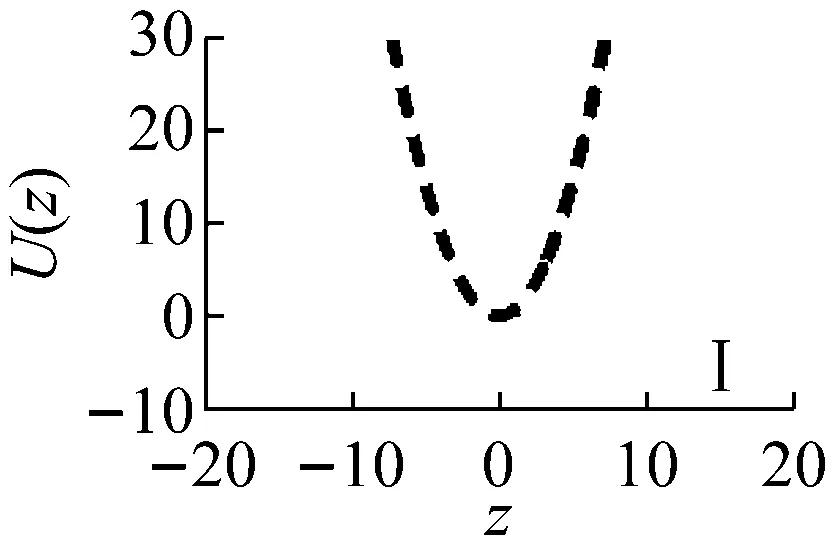
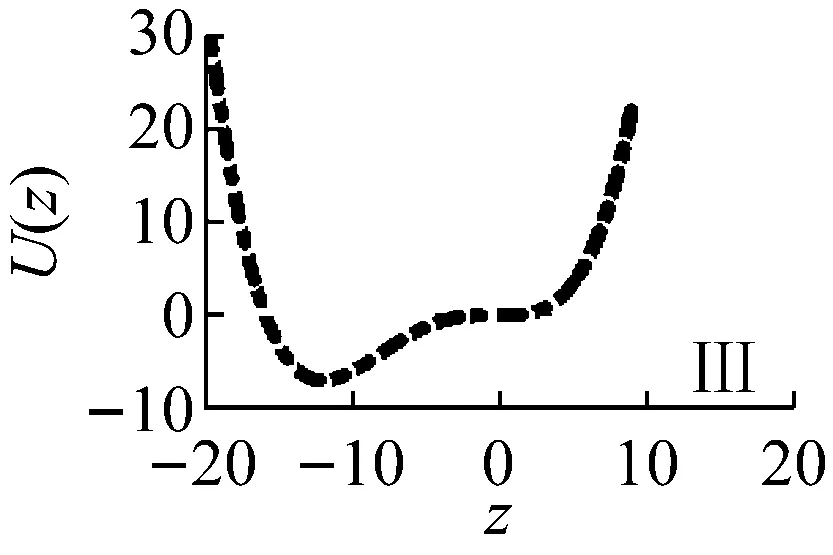
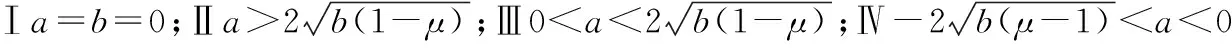
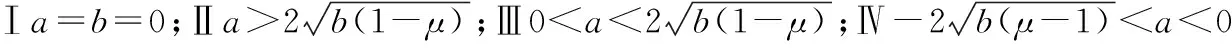
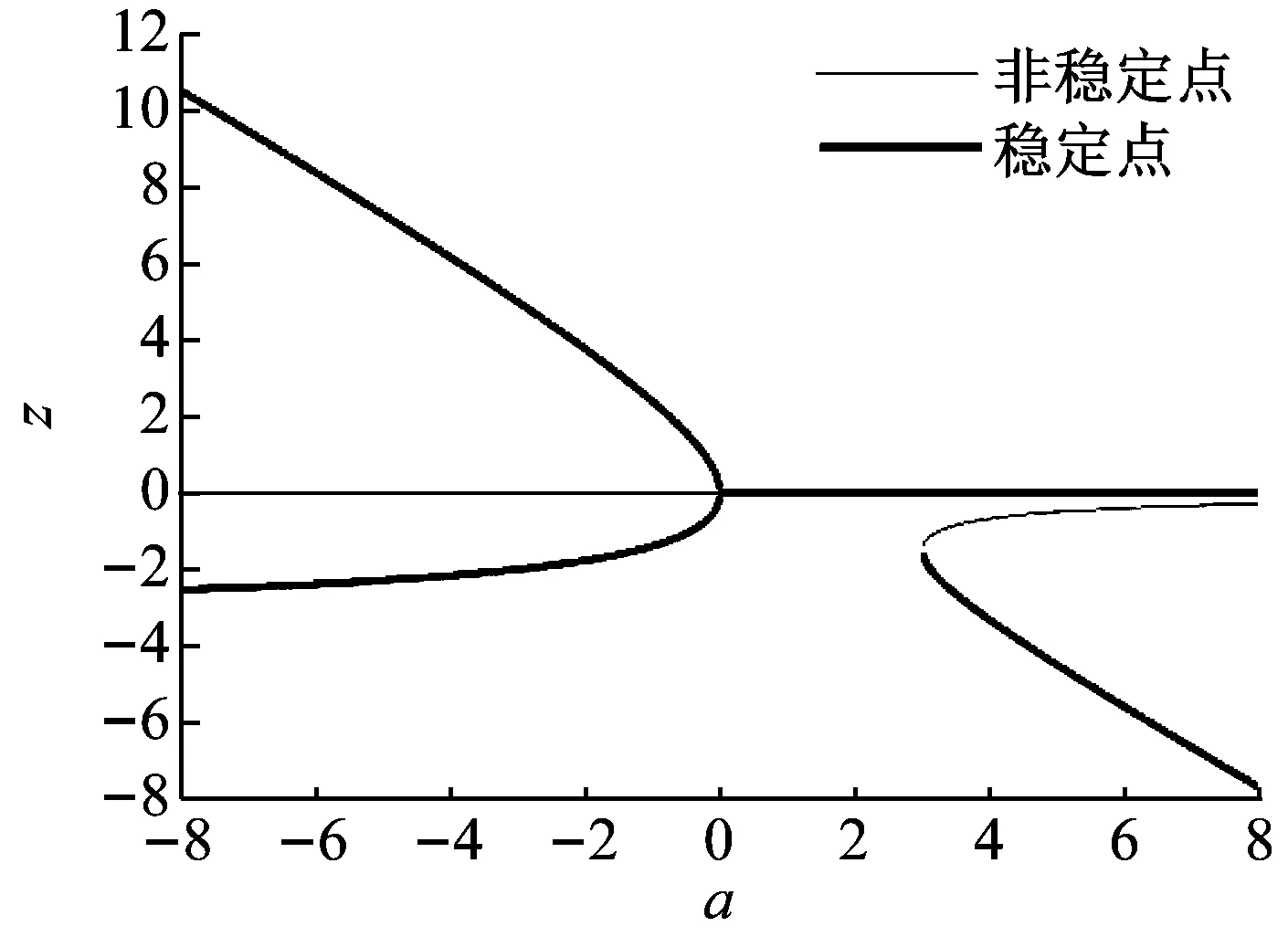
图4 振子静态分岔图
2 系统物理参数
为深入研究系统的非线性运动特性,完善系统振动控制方程,本节将阐述磁力、薄膜回复力、系统等效质量和结构阻尼等物理参数的获取过程。
2.1 磁力仿真
错综复杂的磁场导致两磁体之间缺乏精确的磁力解析式,常规意义下基于磁偶极子磁密度理论的磁力解析式仅适用于磁体能简化为质点的情况[16],而进一步的实验及数值分析都表明:采用该解析式计算BEMH的磁力,所得结果误差较大,进而影响结构势能函数与平衡点位置的分析。为提高准确性,本文采用Ansoft Maxwell进行磁力仿真,此软件是电磁场分析软件,广泛用于工业电磁元件,如传感器,调节器,电动机,变压器,以及其他控制系统的设计,能够真实有效地模拟电磁场,并采用三维瞬态场进行仿真。
根据薄膜振子的振动范围,采用立方非线性磁力表达式为基础进行仿真:
Fm=α1z+α3z3
(15)
式中:α1=0.104 978 6 N/mm,α3=5.654×10-3N/mm3。
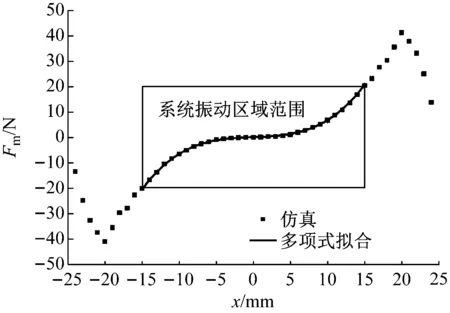
图5 振子磁力曲线
2.2 物理实验
(I) 薄膜回复力分析
将带有薄膜的支撑环垂直固定于实验台(此时y=0,x=z), 为避免重力引起薄膜下垂,测试过程中移除NdFeB磁铁,利用测力计(型号:HP-50)施加、撤除薄膜中心力,同时读取测力计相应位移和力,翻转支撑环,重复上述测试。由图6可知,此薄膜仅存在弹性变形。因曲线始终穿过坐标原点且具有对称性,所以拟合曲线不存在常数项与偶数项,三次多项式很好地拟合了实验数据:
Fr=β1z+β3z3
(16)
式中:β1=0.027 5 N/mm,β3=9.345×10-3N/mm3。
(II) 结构阻尼和线性固有频率分析
为识别系统结构阻尼和线性固有频率,将BEMH垂直固定于实验台(消除重力引起薄膜的初始位移,此时y=0,x=z),对系统施加初始位移,并采用激光位移传感器(型号:KEYENCE IL-065)测量其衰减振动。基于振动基本原理[25]可获得欠阻尼线性系统的响应:
z(t)=Ae-ξωn0tcos(ωdt-φ)
(17)
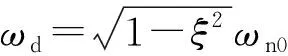
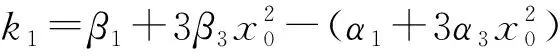

(a) 回复力实验图
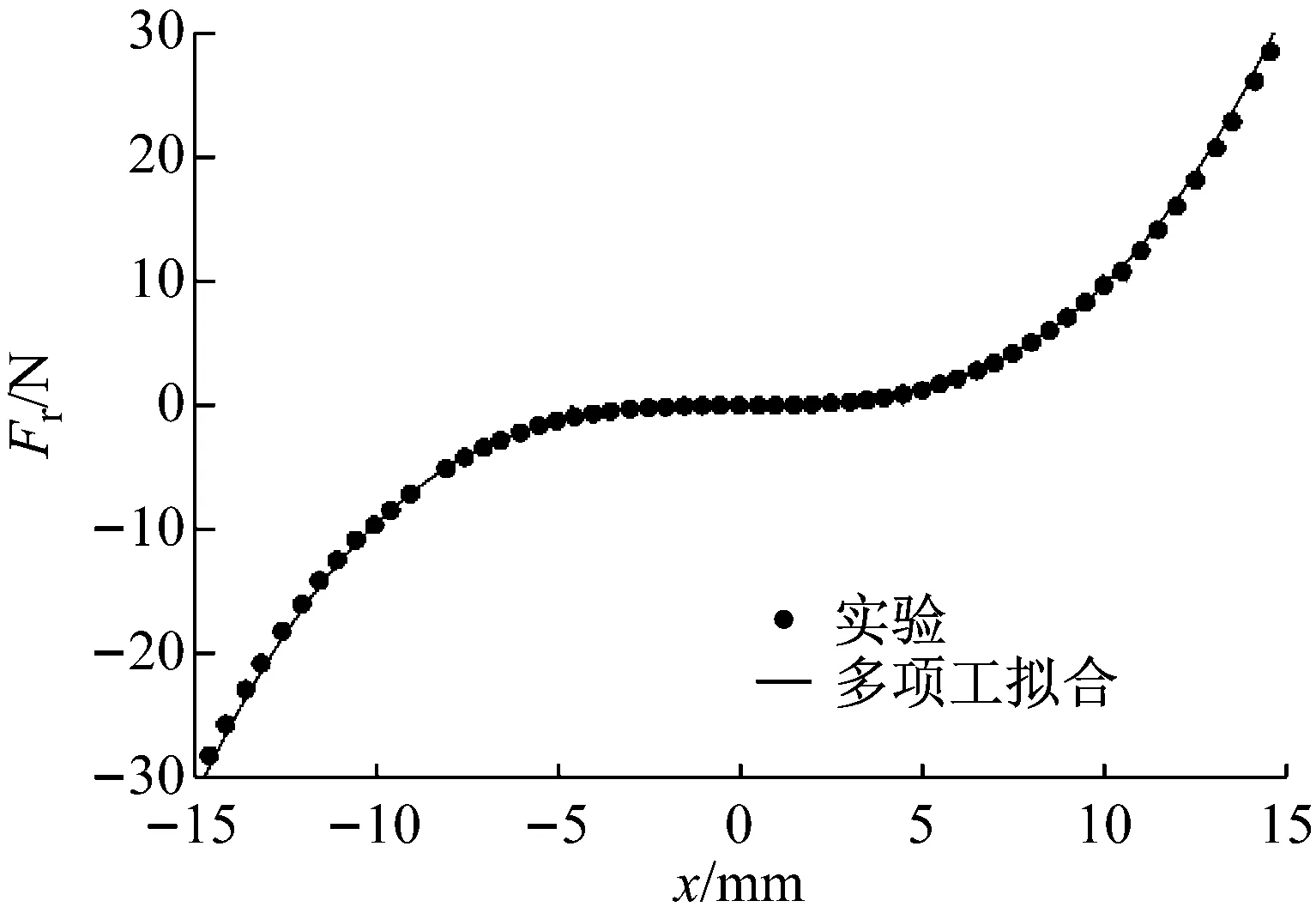
(b) 回复力曲线图
最终可得系统的基本物理参数,见表1。

表1 BEMH物理参数
3 EMH与BEMH模型对比
3.1 势能曲线
去掉样机上下端盖处的氧化铁芯(保留线圈绕组),BEMH将变为传统的单稳态振动能量采集器(EMH)。由图7可知相对于EMH,BEMH存在较浅的能量阱,可以跨越势垒产生大幅阱间运动。因此,BEMH更适用于外界复杂激励环境。
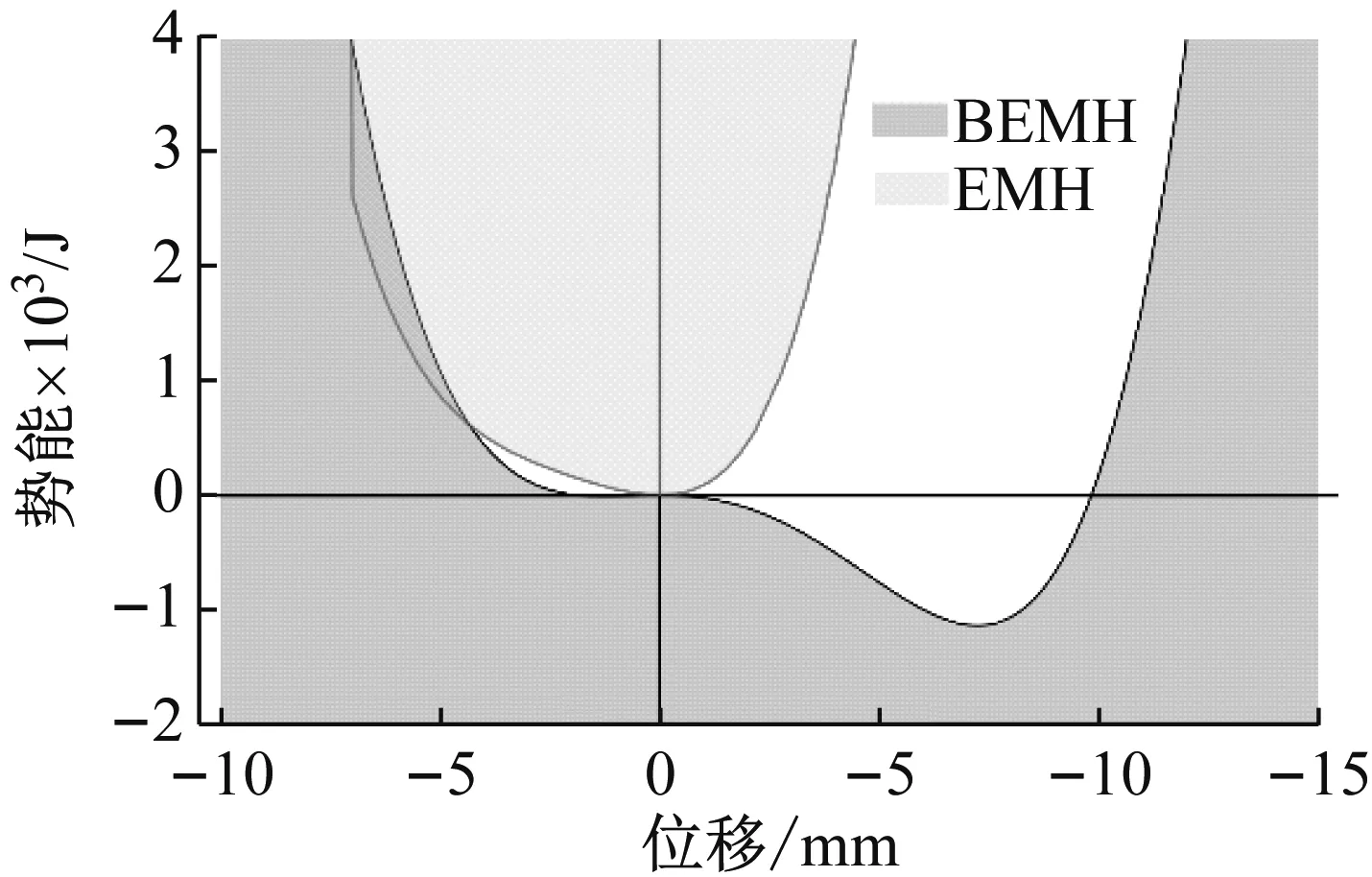
图7 振子势能曲线图
3.2 数值模拟
根据振动控制方程式分析EMH与BEMH处于不同外界加速度条件下,基础激励频率在0.01~25 Hz范围内的位移响应(系统参数取值如表1所示)。图8给出了两种初始条件且不同外界加速激励时,BEMH和EMH的幅频响应图。
(1) 外界加速度为0.16 m/s2时,由图8(a)得EMH的共振频率为8.50 Hz,单稳态的性质决定其幅频曲线只存在稳定且相对较高的峰值(C点),且峰值位置与初始条件无关。因为BEMH没有足够的能量逃离势阱,只能在两个平衡点附近做周期运动(即A,B两点分别对应的曲线),所以BEMH的幅频图存在两个相对较小峰值(A,B点)。虽然EMH的共振幅值优于BEMH,但其有效工作频带低于BEMH。
(2) 外界加速度为4.9 m/s2时,由图8(b)可得BEMH产生阱间运动的频带为5~10 Hz,与此同时EMH的工作频带为5.2~10.3 Hz,由此可见非线性磁力的存在使得BEMH的带宽向低频区域移动。虽然BEMH和EMH的有效频带宽度接近,但BEMH幅值增长速率明显优于EMH。
(3) 外界加速度提高到7.84 m/s2,从图8(c)可以看出,两个能量采集器的工作频带和运动幅值继续增加,但BEMH的有效工作频带拓展的更宽(4.8~12.9 Hz)。
(4) 外界加速度达到11.76 m/s2时, BEMH的频带以固有频率为基点向左右两个方向扩展,左方区域从3.57 Hz开始做大幅阱间运动,右方区域至19.64 Hz结束大幅阱间运动。BEMH的幅值平稳增长最后趋近于定值,这是由于幅值增加导致结构整体回复力增大,限制NdFeB磁铁在两个平衡点之间做阱间运动,即:随外界加速度的增加,BEMH运动幅值将不会进一步增大。
4 实 验
4.1 实验装置
图9显示了实验设备和能量采集器样机。实验仪器主要由信号发生器(型号:Tektronix AFG3102C)、信号功率放大器(型号:ZD-G-800)、激振器(型号:Brüel & Kjr LDSV850)、数字存储示波器(型号:Tektronix DPO2012B)、加速度传感器(型号:Brüel & Kjr 8344)等组成。
信号发生器产生的正弦信号经过功率放大器及激振器作用于样机,迫使样机薄膜振子振动,并利用加速度传感器监测样机加速度信号,同时通过示波器采集样机的输出电压。实验过程中通过移除样机上下铁芯得到EMH,从而进行输出性对比。
4.2 实验结果
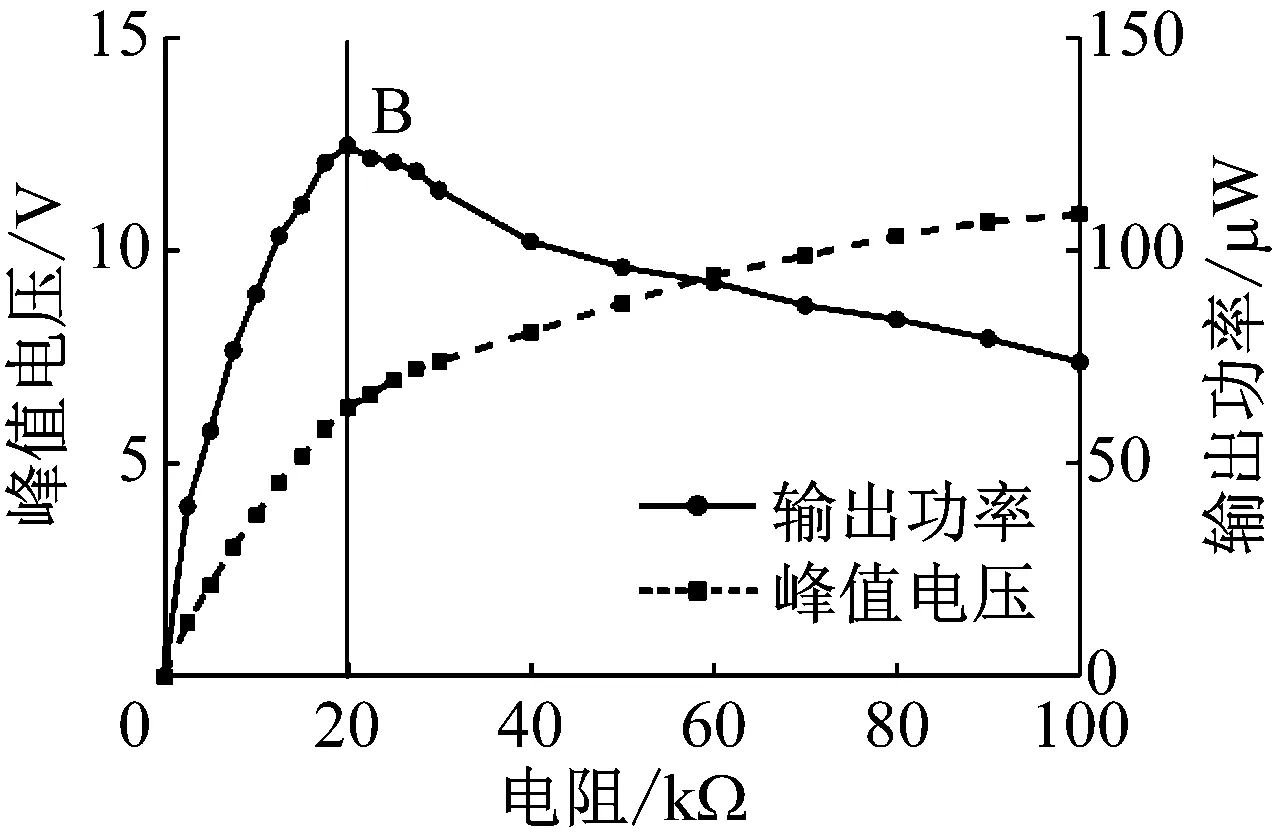
当基础激励加速度为11.76 m/s2,且处于主共振时,EMH和BEMH的峰峰值电压及输出功率与负载电阻之间的关系曲线,如图10所示。在负载电阻初始增加阶段,两个能量采集器的输出电压迅速增大,然后随着负载电阻的继续增加,输出电压增长趋势缓慢,直至出现饱和状态,这是由于负载电阻已经远远超过线圈内阻。与此同时,随着负载电阻的增加,输出功率迅速增大到功率极值(A,B点),对应电阻值7.8 kΩ,20 kΩ,然后迅速减小。
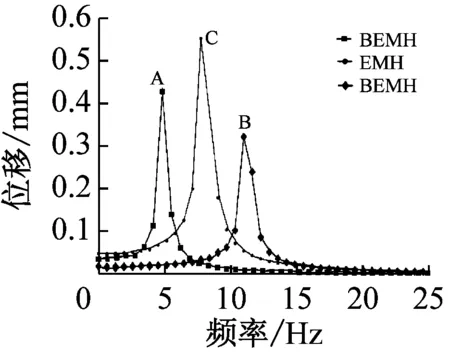
(a) A=0.16 m/s2
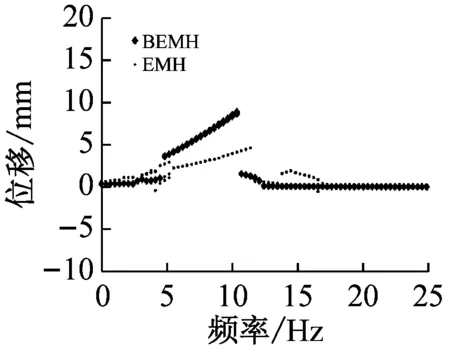
(b) A=4.9 m/s2

(c) A=7.84 m/s2
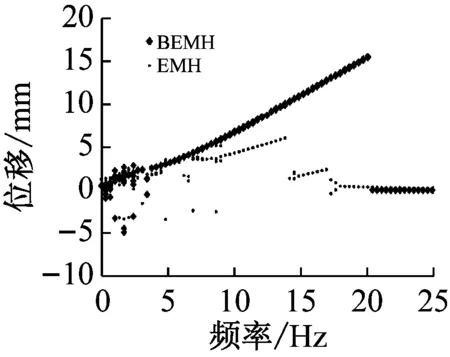
(d) A=11.76 m/s2
图8 BMEH和MEH的幅频响应图
Fig.8 Amplitude-frequency response of the BMEH and the MEH
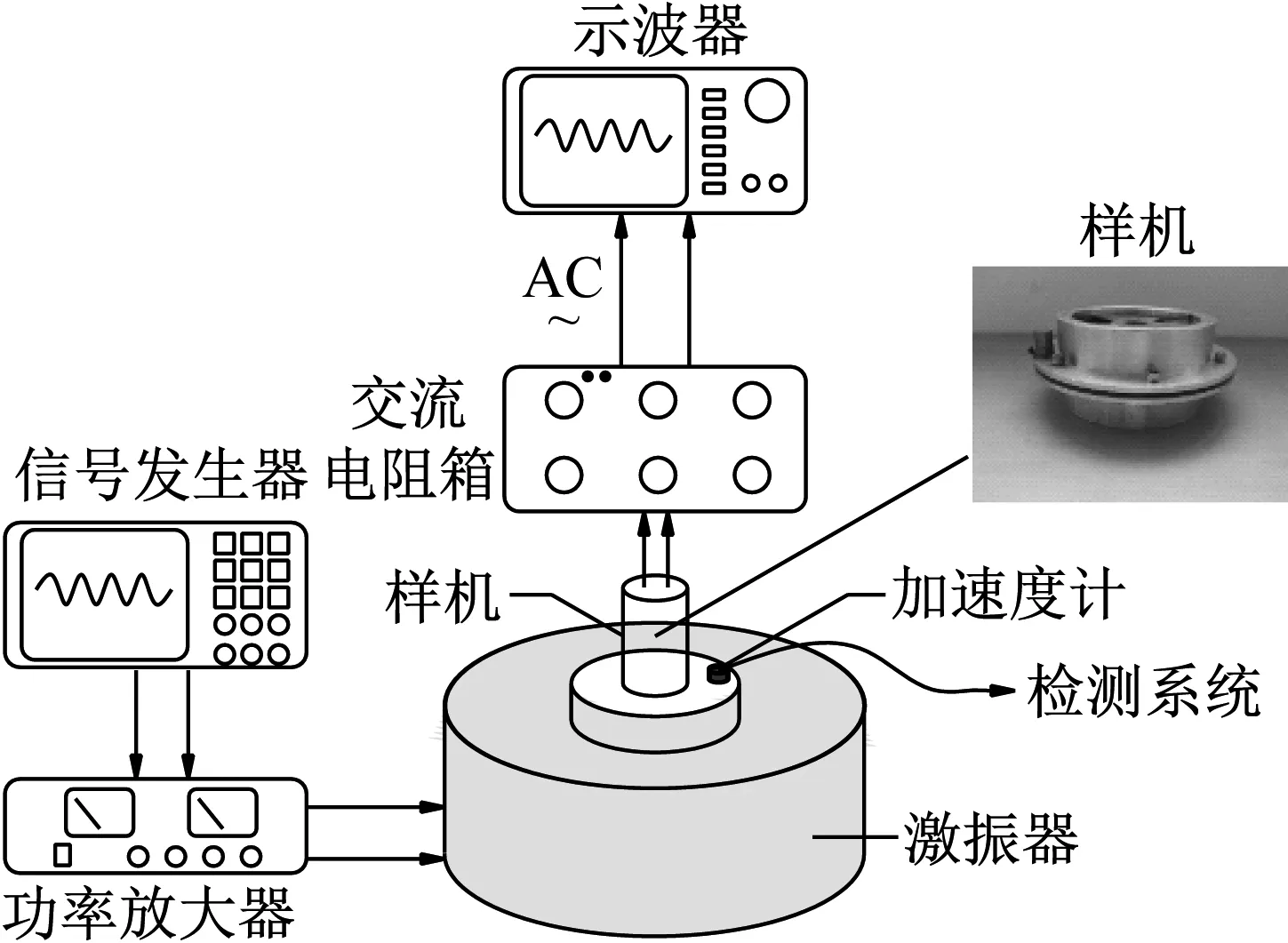
图9 实验装置及流程

(a) EMH
(b) BEMH
图11分别显示了不同基础激励加速度及外接最优电阻条件下,BEMH和EMH在0.01~25 Hz范围内的输出功率。随着激励幅值增加,EMH和BEMH的工作频带逐渐拓宽,薄膜低刚度的特点使得能量采集器灵敏度较高;BEMH结构中包含的磁铁弹簧使其出现双稳态运动形态,有效工作带宽同时向线性固有频率两侧拓宽。在相同外界激励下,BEMH的阱间运动使得其输出功率较高,接近EMH的16倍(外界激励为11.76 m/s2,激励频率为15 Hz)。随着外界加速度值进一步增加,EMH和BEMH的输出功率逐渐提高,BMEH的双稳态特性限制其最终在两个平衡点之间运动,使得BEMH的输出功率逐渐趋于稳定值。
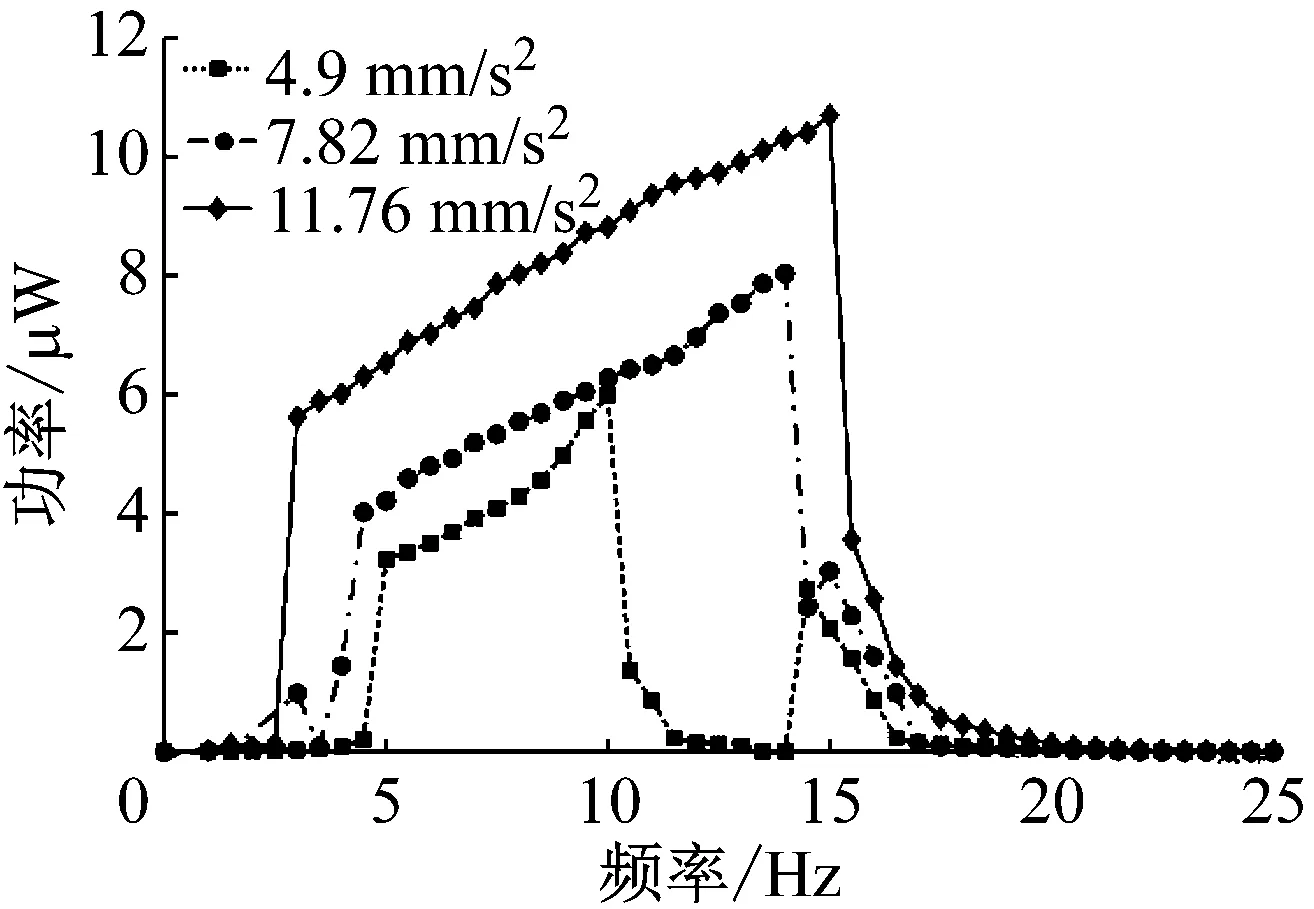
(a) EMH

(b) BEMH
5 结 论
本文提出了一种能感应低频小幅环境振动且具备较宽工作频带的双稳态电磁式薄膜振动能量采集器,并对其进行了理论分析、数值模拟以及实验验证。结果表明:
(1) 建模过程中考虑薄膜大变形回复力表达式是非常必要的,为后续从理论上指导样机改良提供了可供参考的依据。
(2) 双稳态运动相较于单稳态运动,运动幅值较大,相对速度增加,能量采集效率显著提高,工作频带有效扩展。
(3) 磁力弹簧的介入使得薄膜式振动能量采集器整体刚度较小,灵敏度提高,更适用于日常生活中的低频振动环境。

