油浸式自耦变压器振动噪声研究

鲁文波， 曲光磊

(1.上海海基盛元信息科技有限公司，上海 200235； 2.特变电工沈阳变压器集团有限公司，沈阳 110025)

近年来电力变压器的容量等级逐渐提高，产生的振动噪声问题日趋严重，振动噪声已成为电力设备产品和市场需求的重要指标。变压器振动不仅影响电力设备正常运行和使用寿命，也导致了环境噪声污染，科学地解决变压器振动噪声问题已成为变压器生产厂家与使用部门亟需解决的难题。变压器振动噪声模拟涉及磁致伸缩、磁固耦合、流固耦合等建模与计算，考虑磁致伸缩的振动噪声分析一直是行业难点。目前研究手段主要以试验分析[1-3]和工程治理[4-5]为主，在绕组状态监测方面也有较多研究[6-7]，但仿真模拟主要集中在激励力简化计算、振源等效[8-10]与绕组振动分析[11-12]。其中，文献[10]用数组点声源组成的声学系统等效模拟油箱壁振动所辐射的噪声，得到远处测试点的噪声水平与实际基本相符，为后续有源降噪研究提供方便，文献[11]通过对大型变压器绕组有限元建模与分析研究了绕组预紧力与箱壁振动之间的关系，文献[12]基于“磁-机械”耦合场理论实现了变压器运行过程中由电动力激励到绕组振动响应的全过程仿真分析，而考虑铁心磁致伸缩的研究较少，变压器振动噪声问题还有待深入研究。

变压器激振源包含铁心磁致伸缩、绕组洛仑兹力及铁心接缝处的表面电磁力，铁心构件采用斜接缝、步进式、重叠搭接等先进制造工艺，使得铁心内部漏磁很小，电磁力也很小，空载工况下表面电磁力与绕组洛仑磁力引起的振动与磁致伸缩效应产生的振动存在数量级上的差异，可以忽略，变压器本体振动主要由铁心硅钢片磁致伸缩引起[13-15]。变压器铁心硅钢片的磁致伸缩不但与磁场具有复杂的非线性关系、存在各向异性，还受制造工艺、运行状态及环境等多种因素的影响，是一个非常复杂的现象，至今学术界尚未统一建立可准确反映磁致伸缩特性的数学模型。铁心引起的器身振动经过紧固件、垫脚以及变压器油传递至油箱，进而辐射噪声。目前多采用调节夹紧力、改变油箱结构等经验措施进行降噪，为了从机理上进行分析，探索科学有效的降噪方法，考虑磁致伸缩效应的变压器振动噪声分析是必要的。

本文针对某大型油浸式自耦变压器振动噪声超标问题，利用商用有限元软件建立变压器三维电磁场模型，求解瞬态场得到不同时刻铁心硅钢片各节点处的磁通密度；再将磁致伸缩与热效应相比拟，通过等效处理相关物理量建立磁致伸缩等效模型，实现铁心磁致伸缩位移计算，以此作为激励计算器身振动；考虑变压器油的传递，建立器身-变压器油-油箱的流固耦合模型，计算变压器整机振动，进而计算辐射噪声，并与实测值相比；同时还分析了油箱加筋与油箱壁厚度变化，以及油箱底部约束方式对振动噪声的影响，为变压器降噪提供了参考。

1 理论基础与计算流程

1.1 电磁场理论基础

基于Maxwell方程，忽略铁心涡流效应，变压器铁心区域瞬态电磁场方程可表述为：

(1)

1.2 振动理论基础

通过三维瞬态电磁场求解，可得到铁心不同时刻铁心硅钢片各节点处的磁通密度，再结合磁致伸缩等效模型得到铁心磁致伸缩位移，以此作为激励源可进行器身强迫振动分析，满足如下动力学方程：

(2)

1.3 声学理论基础

采用声学有限元法求解声学Helmholtz方程来计算声场。通过声波的连续方程、运动方程和物态方程可推导得到Helmholtz波动方程[16]，通过傅里叶变换可得均匀流体中传播的基本声学方程频域形式为：

(3)

式中:k为波数，k=ω/c=2πf/c，m-1，其中，c为声波在流体中的速度，m/s；ρ0为流体密度，kg/m3；q0为外部作用于流体的质量源。

1.4 变压器振动噪声计算流程

空载工况下变压器的振动噪声研究主要考虑由磁致伸缩现象引起的铁心振动，相关仿真计算涉及电磁、流体、结构、振动、声学等多个学科，特别是铁心磁致伸缩计算与磁固耦合、流固耦合的多物理场建模计算，计算流程包含瞬态电磁场计算、铁心磁致伸缩计算、器身与整机电磁振动计算、整机噪声计算等。如不考虑冷却系统产生的噪声，油浸式变压器振动噪声计算流程，如图1所示。

图1 油浸式变压器振动噪声计算流程

2 电磁场建模与计算

2.1 分析工况

电磁仿真主要是通过有限元方法求解Maxwell方程组，得到所需的磁通密度、电磁力和电流密度等参数的分布和大小。变压器电磁场仿真分为空载和短路工况，在空载状态下，主要是铁心励磁，此时振动噪声主要由铁心磁致伸缩产生；在短路状态下，振动噪声主要由绕组短路电磁力产生。大量试验证明，空载状态下铁心振动产生的噪声远高于短路状态下绕组振动产生的噪声[17-18]，故本文以空载状态为分析工况，对铁心磁致伸缩所产生的振动噪声进行分析研究。采用Ansys软件实现电磁场与电磁振动的仿真计算，采用Virtual.Lab Acoustics软件实现辐射噪声的仿真计算。

2.2 电磁场建模

本文对某自耦变压器(型号：ODFPS-334500-500)进行电磁振动噪声的详细建模计算与分析，其三维几何模型如图2。

图2 自耦变压器三维几何模型

为提高计算精确度，需根据不同部位精细化程度分区域进行剖分，完成三维实体有限元建模。其中，铁心建模需根据铁心截面形状尽量分级，保证截面积一致；绕组建模需根据绕组位置及具体内外径进行等效建模(本文等效为圆柱筒)。考虑后续磁固耦合计算的便捷性与数据传递的准确性，铁心建模时考虑了器身垫脚(由工字钢、层压木与胶垫构成)与夹件等约束结构。在铁心及绕组外面包围空气包，尺度为器身大小的5倍，由于器身沿长轴方向完全对称，故采用1/2对称分析。电磁场分析中主要材料属性设定，如表1所示。

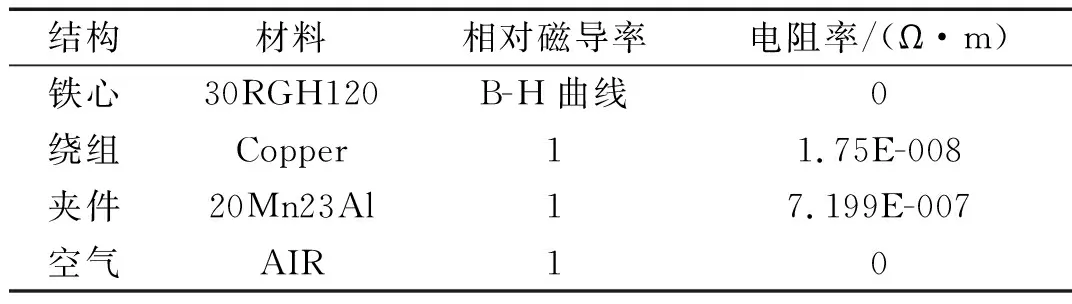
表1 主要材料属性(20 ℃)

电磁场有限元建模时，绕组采用六面体网格，铁心采用四面体网格，网格划分需根据模型尺寸大小来确定疏密，保证网格渐进与平滑，节点总数为559 090，单元总数为356 188。施加激励为电流密度，在高压绕组上加载额定电流为1 101.9 A的励磁电流，串联匝数为424，励磁电流比例为0.09%，线电压525 000 V，相电压303 109 V。设置计算时间步为0.04 s，选择空气包的6个外表面，施加磁力线平行边界条件。

2.3 电磁场计算结果

求解三维瞬态电磁场得到磁场分布，其中磁通密度矢量分布如图3所示，铁心中心磁通密度约为1.74 T，计算单设计值为1.76 T，验证了磁场仿真的准确性。铁轭上某点处的磁通密度时域曲线如图4(a)所示，平顶波形表明该处磁场出现饱和，经FFT后得到频域曲线如图4(b)所示，可以看出主要能量集中在50 Hz处。

施加电流频率为50 Hz，电磁力频率则变为100 Hz，即加载电流的2倍；在仅有励磁电流的情况下，铁心中的电磁力很小，可忽略不计，变压器空载下的振动噪声主要由铁心磁致伸缩引起。

图3 磁通密度矢量分布(t=0.005 s)

(a) 时域曲线

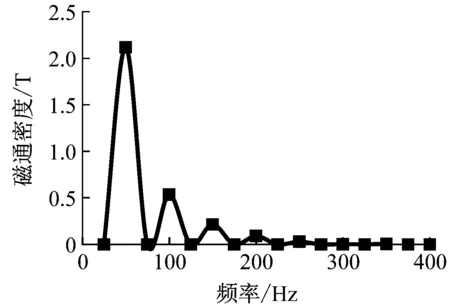
(b) 频域曲线

3 铁心磁致伸缩计算

3.1 磁致伸缩等效模型

变压器铁心励磁在宏观上表现为硅钢片在沿着磁力线方向的尺寸增加，而垂直于该方向的尺寸缩小，即磁致伸缩现象，磁致伸缩大小常用其长度相对变化量表示，即磁致伸缩系数或磁致伸缩率：λ=ΔL/L，L为原始尺寸，ΔL为最大形变量。磁致伸缩率受诸多因素影响，很难完整地建立一个合理描述的理论模型，一般借助实验手段使用激光位移计来测量铁磁材料的磁致伸缩率。通过对不同磁场作用下的磁致伸缩进行测量[19-20]，得到一系列磁通密度与磁致伸缩率之间的对应关系，将这些数据绘制成曲线即得到磁致伸缩特性曲线，典型磁致伸缩特性曲线如图5所示。测量表明，硅钢片铁心磁致伸缩是非线性的[20-21]，因此变压器铁心产生的振动噪声与磁通密度之间也呈现一种非线性关系。

图5 典型磁致伸缩特性曲线

铁心结构处于复杂的交变磁场环境，不仅受到磁场本身及磁致伸缩效应的影响，同时也影响所处的磁场以及材料本身的磁化，由此引起复杂的磁固耦合问题。本文借助商用有限元软件，基于耦合场分析将磁致伸缩效应与热效应相比拟，通过铁心节点磁通密度插值磁致伸缩特性曲线，应用于磁固耦合模型，实现铁心硅钢片磁致伸缩的数值计算。

热弹性力学物理方程可表述如下：

(4)

式中，σx、σy、σz为正应力分量；τxy、τyz、τzx为剪应力分量；εx、εy、εz为正应变分量；γxy、γyz、γzx为剪应变分量；E为弹性模量；μ为泊松比；α为热膨胀系数；T为温度；下标x、y、z表示笛卡尔坐标方向；下标xy、yz、zx表示笛卡尔坐标平面。

磁弹性力学物理方程可表述如下：

(5)

式中:Hx、Hy、Hz表示磁场强度H的三个方向。

比较式(4)与式(5)可知，磁致伸缩效应与热效应在物理方程上形式相似，若将两式中的相应参数与物理量作如下等效处理：

(6)

即将磁弹性力学中的磁致伸缩率系数与磁场强度分别比拟为热弹性力学中的热膨胀系数与温度，则两个方程所描述的物理问题转化为同一形式的数学方程，从而有限元控制方程也具有相同表现形式。所以，将磁致伸缩效应与热效应相比拟，在物理现象本质和物理方程上是可行的，其推导简捷，物理意义明确，输入输出变量可参考耦合分析处理方法。

3.2 磁固耦合与磁致伸缩位移计算

为了便于磁固耦合计算与数据传递，铁心结构有限元模型直接来自磁场模型。考虑铁心构件的各向异性属性，通过模态计算与测试分析得到铁心构件力学参数，铁心模态测试,如图6所示。

图6 铁心模态测试

将计算到的磁通密度经FFT后得到频域下的磁通密度分布，通过有限元单元上的节点插值到磁致伸缩特性曲线，得到对应节点上的应变数值，采用等效模型将应变作为比拟法计算的基础参数，取假定的热膨胀系数和初始参考温度(本文分别取1.1E-5/℃和20 ℃)，得到硅钢片区域各节点上的最终温度，并以此结果作为热分析的节点温度载荷，通过热比拟计算即可得到节点位移，实现铁心磁固耦合计算。得到各频率处的铁心磁致伸缩位移如图7所示(以50 Hz为例，磁致伸缩后频率变为100 Hz)，图(a)～(c)分别表示100 Hz、200 Hz、300 Hz处振动，其中，100 Hz处振动最明显，最大振幅值为5.05 μm，200 Hz、300 Hz处最大振幅值分别为0.076 9 μm、0.003 38 μm，随着频率增大其振动能量依次降低，与磁通密度结果一致。

4 变压器振动计算分析

4.1 器身振动计算

采用插值方法通过APDL命令流将铁心振动位移加载到器身模型的铁心上，计算得到器身整体振动，振动云图如图8所示，图(a)～(c)分别表示100 Hz、200 Hz、300 Hz处振动(单位：mm)。

提取主要频率处器身振动的最大值如表2所示，振动形态与铁心类似，基频100 Hz处的振动远大于其

图7 铁心磁致伸缩振动

Fig.7 Magnetostriction vibration of iron core

(a) (b) (c)

表2 各频率处器身振动值比较

他频率，最大振幅值为5.05 μm，主要振动位于上下铁轭、旁柱、上下铁轭接缝处。由于激励频率与器身某些模态频率接近，也存在局部频率振动，整体振动重点关注100 Hz即可。

4.2 流固耦合与整机振动计算

油浸式变压器振动分析需考虑变压器油的能量传递，通过建立器身-变压器油-油箱的流固耦合模型，将器身振动能量通过变压器油传递到油箱上。流固耦合建模时将器身结构与流体单独划分网格，在二者交界面上通过APDL命令流方式建立流体与结构网格的接触连接。该方法不需要器身结构与流体共节点，大大简化了网格划分的工作量与难度。设定声音在油中的传播速度为1 400 m/s，油的密度为900 kg/m3。将铁心振动结果通过节点坐标插值到该流固耦合模型中，计算得到变压器整体振动情况如图9所示，图(a)～(c)分别表示100 Hz、200 Hz、300 Hz处振动，单位：mm。与铁心、器身振动情况类似，100 Hz处振动最大，其最大振幅为0.016 79 mm，200 Hz、300 Hz处最大振幅分别为0.067 5 μm、0.028 18 μm，随着频率增大变压器振动依次降低。

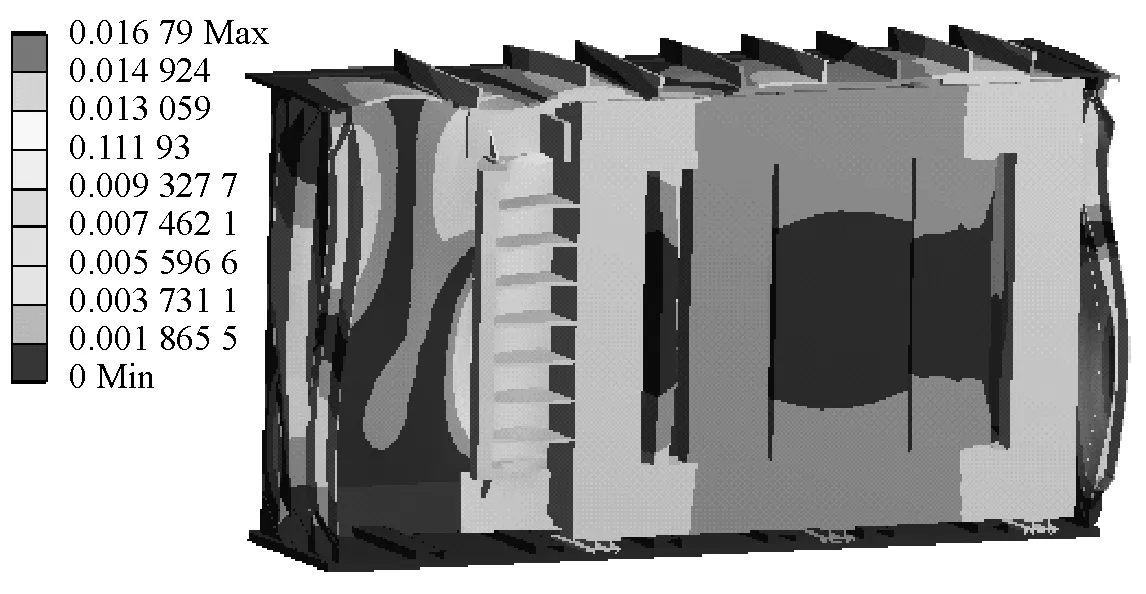
(a)

(b)

(c)

从整机振动结果分析可知，该自耦变压器在空载工况下主要表现为100 Hz处的振动，振动形态为铁心振动带动器身振动，再通过变压器油与器身连接构件的传递，引起油箱整体振动，同时由于油箱局部模态与激励频率接近出现局部较大振动，另外，高次谐波产生的振动很小，后续进一步考核噪声结果。

5 变压器噪声计算分析

以油箱壁的振动计算结果作为噪声计算的输入，在外场进行变压器的声辐射计算。噪声模型的网格可从振动分析中的油箱结构网格导出，提取油箱振动结果，加载到油箱表面(声场网格)，建立噪声计算模型，进行声辐射计算。测量基准面距离油箱壁为0.3 m，通过插入场点模型的方式建立场点网格，计算得到噪声分布如图10所示(单位：dB，以100 Hz为例)，主要频率处噪声最大值如表3所示，高次谐波产生的噪声相比100 Hz处要小10 dB以上，可忽略不计。

图10 变压器噪声分布

Tab.3 Noise comparison of transformer at various frequencies

参数数值频率/Hz 100200300声压级/dB70.144.546.2

在变压器高度的1/3与2/3位置每隔1 m取一个噪声监测点，共22个监测点，各测点在100 Hz处的噪声计算值,如表4所示。

表4 各监测点处变压器噪声计算值

(7)

式中:Lpi为各测点噪声值；i=1,2,…,22，为测点编号。经试验站测试，该台变压器产品的实测噪声平均值为60 dB，仿真计算与实测结果吻合较好，验证了本文所建立的磁致伸缩等效模型的合理性与振动噪声模型的正确性。产生误差的原因主要有：振动计算的约束边界难以与实际情况一致、铁心材料与绕组模型存在等效误差等。

6 变压器降噪措施

6.1 油箱结构改进

改变油箱结构是变压器企业常用的降噪措施，根据实际工程经验，油箱壁加强筋的布置及箱壁厚度对噪声均存在一定影响，目前改进措施主要依据工程经验做定性评估。本文结合所建立的振动噪声计算流程，对油箱结构改进的影响进行定量计算与分析，分别在原油箱结构上增加1道筋、2道筋、3道筋(几何模型如图11所示)和5道筋，加强筋间距分别为1.86 m、1.24 m、0.93 m和0.62 m，得到加筋数量与变压器振动噪声的关系曲线,如图12所示(显示结果为振动噪声最大幅值)。

图11 加3道筋时的油箱结构(1/2模型)

图12 油箱加筋数量与变压器振动噪声的关系曲线

Fig.12 Relation curve between the number of reinforcement rib of tank and the vibration and noise of transformer

可看出，油箱结构差异对变压器振动噪声影响较大，从整体趋势看随着油箱刚度增大，最大幅值先增大后减小。主要原因是加2道筋后油箱固有频率与激励频率接近，引起局部过大振动。加3道筋时局部模态与激励频率也较为接近，但油箱整体刚度增大，相比加2道筋的情况最大振幅有所降低。其中，加2道筋与加3道筋时的含油油箱模态频率如表5所示。随着加筋数量增多，油箱频率增大，远离激励频率，最大振幅逐渐减小。根据油箱振动结果计算得到变压器噪声，其变化规律与动基本一致。根据分析可知，从降噪角度考虑，设计油箱结构时要么“软”一些，布置较少加强筋，要么“硬”一些，布置较多加强筋。

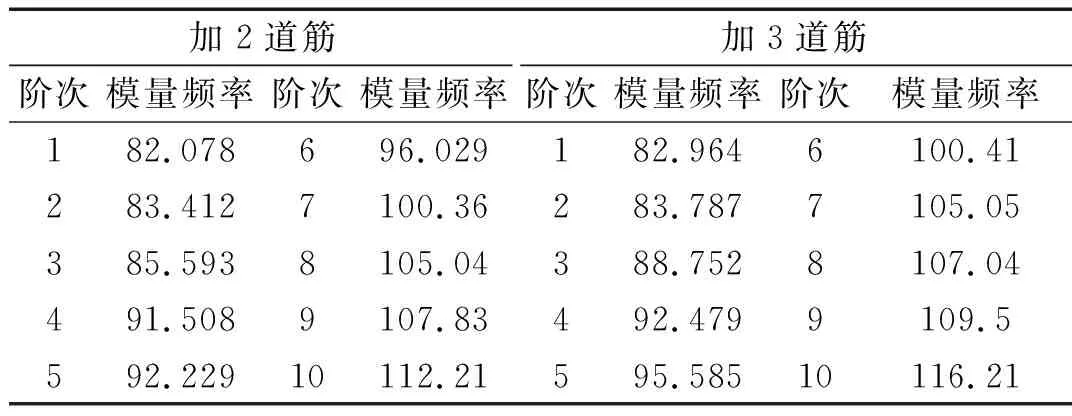
表5 含油油箱模态频率

另外，分析了油箱箱壁厚度与变压器振动噪声的关系，取厚度分别为10 mm、12 mm、14 mm、16 mm和20 mm时的振动噪声计算结果,如图13所示。

图13 不同箱壁厚度与变压器振动噪声的关系曲线

经分析可知，随着箱壁厚度增大，振幅逐渐减小，且油箱振动形态基本一致，但并非线性变化；从趋势上看，随着油箱厚度的进一步增大，振动降低的幅度逐渐变小。箱壁厚度增大则整体噪声也逐渐降低，基本呈线性变化。厚度从10 mm增加至16 mm时噪声最大值降低约2.4 dB(与实际工程经验一致)，从10 mm增加至20 mm时噪声最大值降低约4.4 dB。

6.2 箱底约束方式改进

根据实际经验，变压器安装时箱底约束方式也会对整体噪声造成较大影响，可产生3～5 dB的差异，本文计算分析了三种约束情况下的变压器振动噪声情况：①箱底全约束；②箱底按实际安装情况约束，如图14所示；③改进约束位置，将变压器支撑点(水泥条块)移至器身垫脚正下方。

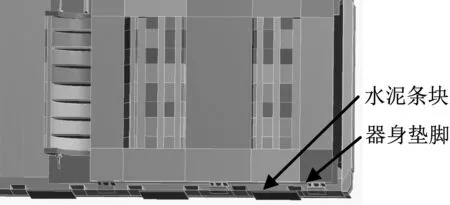
图14 油箱底部实际约束(水泥条块与垫脚未对齐)

经计算分析可知，底部全约束比实际约束情况噪声高约2.3 dB，大量振动能量从箱壁上释放出来，增大了辐射噪声，可见箱底约束并非越多越好。改进后将约束位置调至垫脚正下方，对箱壁内的器身整体起到了较好支撑作用，器身振动得到了有效抑制，整机最大噪声降低近5 dB。

7 结 论

本文建立了油浸式变压器振动噪声的详细分析流程，采用等效模型计算铁心磁致伸缩位移，以此激励计算变压器振动噪声，得出结论如下：

(1) 将磁致伸缩效应与热效应进行比拟，等效相关物理参数，实现铁心磁致伸缩的数值计算是可行的，得到的铁心位移可作为整机振动计算的激励。

(2) 在磁固耦合计算中采用一套铁心模型更为便捷，保证了数据传递的正确性；器身-变压器油-油箱的流固耦合模型充分考虑了振动传递路径，变压器噪声计算值与实测值吻合较好，平均噪声误差为1.5 dB，验证了方法流程的有效性和正确性。

(3) 油箱壁厚度并非越厚越好，要么设计的“软”一些，布置较少加强筋，要么“硬”一些，布置较多加强筋；箱底约束也并非越多越好，容易增大箱壁辐射噪声；将整机约束位置放至垫脚正下方可有效降低噪声。

本文方法流程同样适用于其他油浸式变压器和干式变压器，为深入分析变压器振动噪声问题提供了参考，后续将进一步分析磁通密度、夹紧力、硅钢片材料等对振动噪声的影响。