基于深度图像分析的细粒度矿石分级测定方法

卢才武， 齐 凡， 阮顺领

西安建筑科技大学管理学院，西安710055

矿石粒度大小在碎矿、磨矿、矿物浸出、粉矿焙烧中都是一项重要的参数指标[1].传统的矿石粒度检测主要采用人工采样−机械筛分法、沉降法、电阻法等，但这些方法往往费时费力，且其准确性直接取决于设备质量和操作人员的技术水平，难以满足当前实时高精度的矿石粒度测定需求[2].

近年来，随着图像处理与识别技术的快速发展与应用，已有学者将计算机视觉与图像处理技术引入矿石粒度检测应用.文献[3]将原本利用二维图像计算粒度分布的软件(WipFrag©)加以改进，通过加入表面均匀性特征建立了反向传播(back propagation,BP)神经网络学习下的粒度检测软传感器，可对粒度在50∼90 mm 范围内的矿石颗粒进行识别分类；文献[2]利用矿石表面3D 数据和筛下物的质量建立粒度分类器，该方法对粒度在20∼90 mm 范围内的矿石颗粒有良好的分类效果；文献[4]通过Flashsizer 3D(FS3D)和主成分分析(principal component analysis, PCA)进行矿石粒度分布计算，该方法在40∼70 mm 与20∼40 mm 的粒度检测中的精确率比传统筛分方法分别提高10%与25%.文献[5-8]对矿石图像进行分割和边缘检测，分别提出了不同的改进分割算法与统计算法，以此提取矿石的粒度特征和分布特征进行测量与统计.结果表明：上述方法可以准确测量粒度均匀、颗粒分散、易于分割的矿石颗粒，但对粒度小于10 mm 的细粒度矿石测定误差较大.以上方法主要通过直接获取矿石粒度信息进行分类测定，而没有考虑矿石颗粒之间的强堆叠、强粘连等特点[2]，因此很难通过二维图像直接提取细粒度信息和分布特征，更不能对矿石粒度进行有效测定和分级.有些学者尝试将纹理特征识别用于矿石粒度的分级测定，如文献[9]使用纹理基元算法(texton)、易操纵金字塔算法(steerable pyramid, SP)以及灰度共生矩阵(gray-level co-occurrence matrix, GLCM)这3 种纹理提取算法对煤矿颗粒进行分类测定，但实验的最小矿石颗粒尺寸不小于6 mm.文献[10]首次将纹理特征分析引入5 mm 以下的细粒度矿石检测，采用金字塔算法提取出水力旋流中潜流样本图像的纹理特征，并通过纹理特征结合统计校正模型建立分类器，实现了对进入矿浆的细微颗粒的粒度分类，但该方法仅对矿浆纹理进行识别分类，并未成功应用于矿石颗粒的分级测定.

综上所述，本文综合考虑细粒度矿石颗粒的强堆叠、强粘连等特点，依据自适应灰度共生矩阵提取细粒度矿石颗粒纹理特征，采用最大线性离散度算法确定GLCM 中的生成距离和灰度等级，通过建立基于支持向量机(support vector machine, SVM)的优化分类模型提出一种基于深度图像分析的矿石粒度分级测定方法.实验结果表明，相比于局部二值模式(local binary patterns, LBP)算法以及快速鲁棒性特征(speeded up robust features, SURF)算法，自适应GLCM 具有更高的精确度，能有效反映细粒度矿石颗粒信息.

1 矿石粒度特征提取优化模型

鉴于矿石颗粒的特征提取是粒度分级测定的基础，本文将采用自适应GLCM 进行矿石颗粒的特征提取.为了检验该算法的有效性，将本文方法与LBP 特征[11]、SURF 特征[12]、原始图像特征的分级测定效果进行了对比.

1.1 灰度共生矩阵特征提取

GLCM 算法根据矿石图像中颗粒与缝隙的局部结构，通过选择合适的统计特征量表达不同粒级间的纹理特征[13]，实现粒度信息的间接描述.

假定矿石颗粒图像的矩阵大小为M ×N，定义g(x,y)为图像矩阵(x,y)点处的灰度值，令i = g(x,y)，j = g(x+dx,y+dy)，其中(dx, dy)表示点对的偏移（由生成距离和偏移方向决定），则灰度共生矩阵为

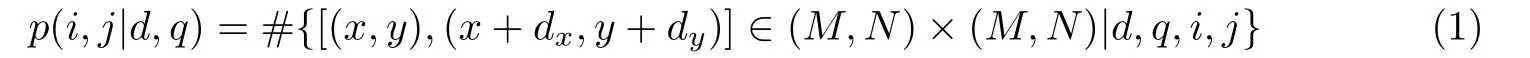
式中，#代表集合中元素的数目；θ 代表偏移角度，通常选取0◦、45◦、90◦、135◦.

生成GLCM 后选取二阶统计量来描述图像特征.本文的特征值如下：

1）能量可用αASM表示为

2）熵可用αENT表示为

3）自相关性可用αCOR表示为

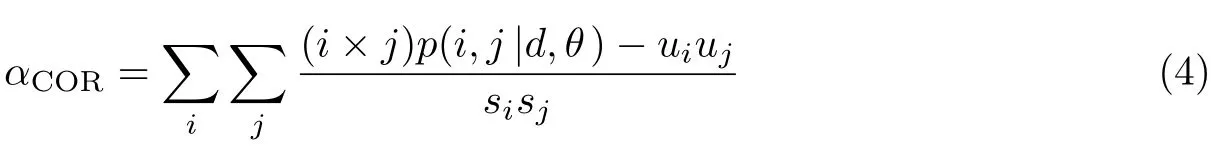
4）对比度可用αCON表示为

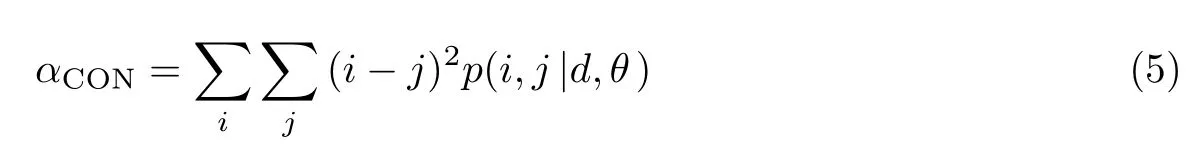
能量、对比度，熵和自相关性是4 种常用的特征值，分别从图像均匀性、粗糙程度、分布差异以及局部模式方面描述粒度信息.因为各特征值互不相干，所以能较全面地分析图像信息[14].

1.2 最大线性离散度自适应优化

数字图像的灰度大小通常为256 个等级，灰度等级越大形成的灰度共生矩阵也就越大，通常采用灰度等级压缩的方法来缩小计算量[15]，而压缩后的图像会失去一些有用信息.因此，在灰度共生矩阵中，生成距离d 和灰度压缩等级m 直接影响图像特征值的区分度和后续分级测定的效果[16-17].传统的灰度共生矩阵通常根据人为经验确定m 与d，但细粒度矿石图像间的特征相似度高，如图3 中不同d 与m 情况下的特征值差异较大，因此人工选择的方法无法保证测定的精度[14,18].若遍历d 与m 的搜索空间提取特征值后再训练不同的分类器，则又非常耗时.

为提高灰度共生矩阵对细粒度矿石颗粒的特征描述能力，本文改进了传统方法中生成距离d 和灰度压缩等级m 的人工选取过程，提出了最大线性离散度自适应选取方法.

假设有N 个粒度等级，i,j ∈N，则各特征值在不同粒度矿石间的线性离散度可以表示为

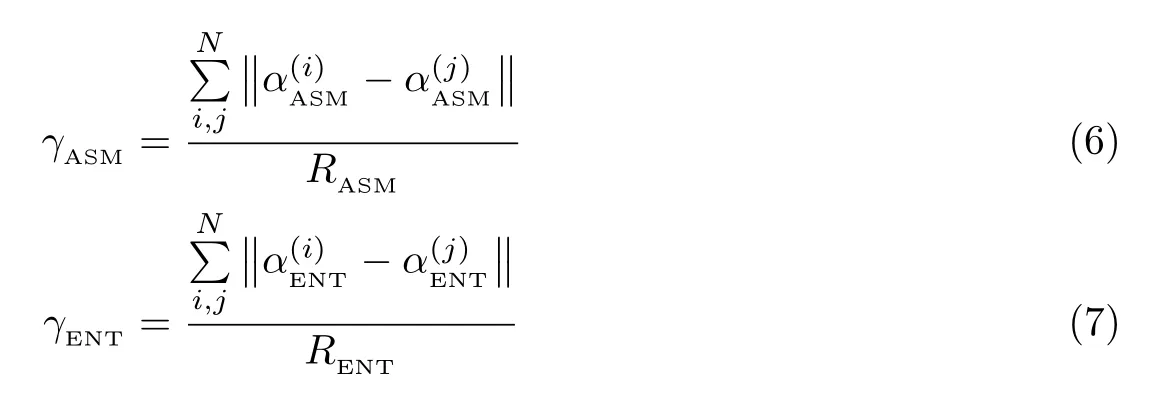
在式(6)∼(9)中，RASM、RENT、RCOR、RCON分别代表不同粒度等级下4 种特征值的极差，αASM、αENT、αCOR、αCON分别代表样本特征值在不同方向上的均值.可以看出，线性离散度是不同粒度等级特征值的曼哈顿距离与类间特征极差的比值，具有最大离散度的数据组在训练特征时收敛速度更快[18]

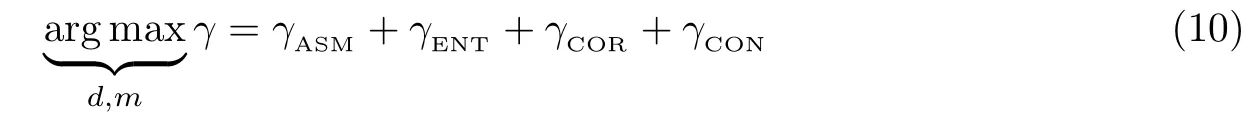
根据矿石图像特征差异程度，根据式(6)∼(10)遍历d 与m 的搜索空间，选取具有最大线性离散度的特征值，实现特性自适应提取.为了便于计算，选取d ∈{1,2,3,4,5,6,7,8}，m ∈{3,8,16,32}，并将每种类别样本的均值作为计算数据.

2 基于GLCM-SVM 的矿石粒度测定方法

支持向量机通过构建最优分割超平面进行样本分类，对小样本分类的精确度很高.采用不同粒度的矿石图片作为训练集，提取GLCM 特征统计量作为SVM 训练集的输入进行训练，算法模型如图1 所示：

具体流程如下：

步骤1输入不同粒级矿石图像并编号.

步骤2将原始图像转化为灰度图，在上述范围中选择不同的d 与m 分别计算0◦、45◦、90◦、135◦这4 个方向的GLCM 和4 种特征值.

步骤3计算4 个方向的特征值均值与标准差并进行归一化处理.

步骤4代入式(6)∼(10)得到最优灰度压缩等级m 与生成距离d 情况下的特征值均值与标准差.

步骤5构建高斯核函数SVM 分类器，每次通过网格搜索法改变参数c 与g 的值.

步骤6使用k 折交叉验证的方法计算正确率，如果正确率大于90%执行步骤7，否则返回步骤5.

步骤7测定测试集样本.

3 实验结果与分析

3.1 实验准备

本文采用煤矿颗粒作为实验对象，根据粒度直径分为4 个等级：0∼0.9 mm，0.9∼3.0 mm，3.0∼5.0 mm，5.0∼7.0 mm.将煤矿颗粒放置于白纸上均匀铺开，采用Canon EOS 80 d 相机进行图像采样，拍摄距离高度为30 cm.实验采样图像大小为1 500×2 000，各粒度级别分别拍摄100 幅共计400 幅图像作为训练集，图2 为采样图像的训练集示例图.实验平台基本配置为i7-6 700HQ，主频为2.6 GHz，内存为8 G；实验软件为Matab 2014a.

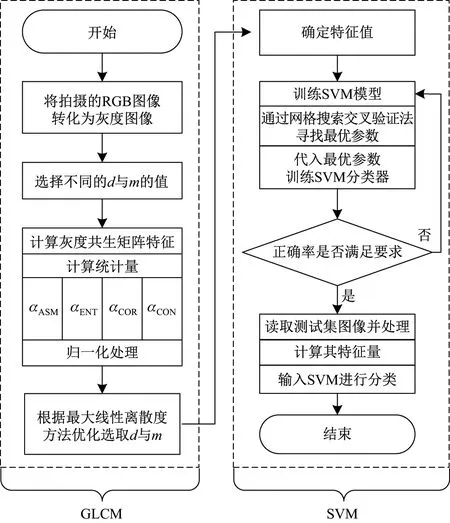
图1 GLCM-SVM 模型图Figure 1 Flowchart of GLCM-SVM model

图2 训练集部分图像Figure 2 Part of pictures on training set

3.2 最优生成距离和灰度压缩等级选取

将不同d 与m 组合下的αASM、αENT、αCON、αCOR代入式(6)∼(11)，求得具有最大线性离散度的d 与m，分别为5 和8.

图3 展示了特征值随d 与m 的变化情况，其中蓝色、红色、黄色、绿色丝带分别代表0∼0.9 mm、0.9∼3.0 mm、3.0∼5.0 mm、5.0∼7.0 mm 这4 种级别矿石颗粒.αASM在m 为8 时与其他灰度等级区分最明显，d 的选取对区分4 种矿石粒度没有太大影响.αENT对m 与d 的变化并不敏感，当m 为8、d 为5 时可以完全区别出4 种矿石粒度.αCON的值大体上随着m 的增大而变小，区分程度也越来越差.当m = 32 时几乎无法区分，当m 为8、d 为5 时可以清晰地区分这4 种粒度.αCOR的变化比较规律，随着m 与d 的增大区分程度逐渐明显.综合看来，当m=8、d=5 时4 项特征值都有很高的区分度，可以充分描述细粒度信息.

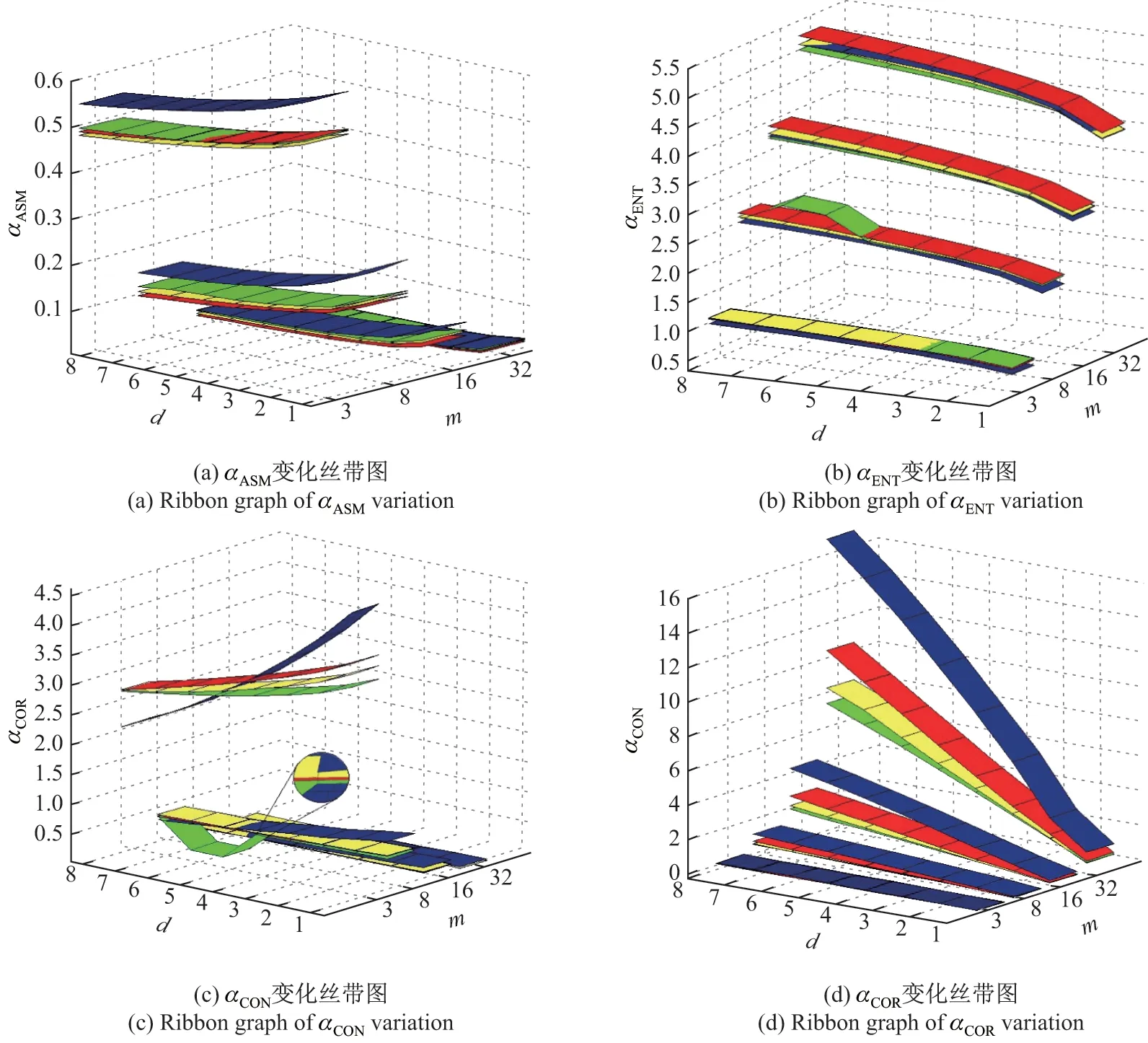
图3 4 项特征值随d 与m 变化的丝带图Figure 3 Ribbon graph of four eigenvalues changing with d and m

传统的灰度共生矩阵主要针对纹理差异图像，人工选定m 的值较大.由图3 可知：当m ∈{3,32}时，特征值中有重合数据，在一定程度上干扰分类测定[14,18]，而最大线性离散度优化算法可以针对细粒度矿石的特性选取最优特征，有效避免数据重合以提高分类精度.

在优化过程中所用数据都是训练集中各粒度等级特征值的均值，而对具体的图像并不能简单地依靠线性离散度进行分类[16].下面依据得到的d 与m 提取特征向量，建立SVM 分类器以实现粒度的精确分级.

3.3 RBF-SVM 特征分类测定结果分析

径向基函数支持向量机（radial basis function-support vector machine, RBF-SVM）对建立非线性软间隔超平面具有良好的适应性，且不依赖大量样本.在RBF-SVM 中，c 的选取会影响分类器的泛化能力，g 的值体现了核函数对样本进行高维映射的有效性[19].为解决c 与g 的选取问题，本文选择网格搜索(grid search)和k(k = 5)折交叉检验算法，在[2−10,210]区间对c 与g 进行寻优[20].

为对比不同特征提取方法的实际效果，分别为原始图像、LBP 特征、SURF 特征和自适应GLCM 特征建立RBF-SVM 进行分类测定实验.不同特征提取方法得到的特征维数相差极大，其中原始图像和LBP 图像均为3×106(1 500×2 000)维，SURF 为500 维，GLCM 为8（2×4）维.为保证分类的时效性，实验时采用PCA 方法将原始图像、LBP、SURF 的特征降低到20 维，然后将分类测定结果与自适应GLCM 进行对比.

4 种特征提取方法经过PCA 降维后的分类超平面可视化效果如图4∼6 所示.

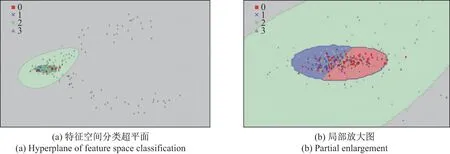
图4 原始图像二维特征分类超平面Figure 4 Hyperplane of 2D feature classification of original image

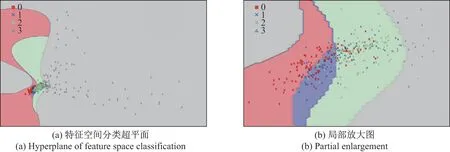
图5 LBP 图像二维特征分类超平面可视化Figure 5 Hyperplane visualization of 2D feature classification of LBP image

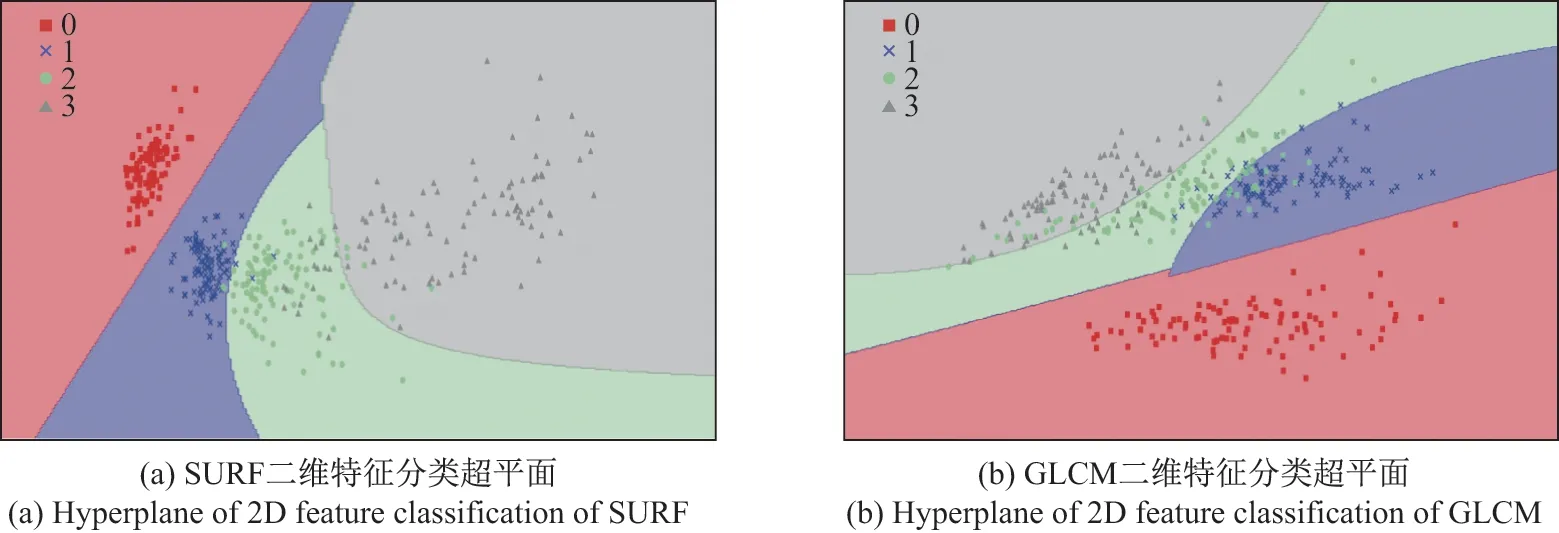
图6 SURF 与GLCM 二维特征分类超平面Figure 6 Hyperplane of SURF and GLCM of 2D feature classification

从图4∼6 中可以看出，原始图像4 种粒度特征相互混合，无法找到一个准确的超平面进行分类；LBP 图像的二维特征聚集在同一尺度范围，超平面的建立同样困难.由此可知，这两种单纯使用图像像素点作为特征值进行分类测定的方法并不可取.在SURF 与GLCM 的可视化结果中，0∼0.9 mm（红色点集）可以清晰地与其他类别区分开，只有少数3.0∼5.0 mm（绿色点集）同0.9∼3.0 mm（蓝色点集）与5.0∼7.0 mm（灰色点集）混合.从二维特征的分类效果可以初步判断原始图像和LBP 图像的分类效果并不理想，这说明SURF 与本文算法更适合细粒度矿石测定.

为进一步分析比对，选取每种粒度等级矿石图像各50 幅共计200 幅进行分类检测，结果如表1 所示.

精确度（precision）可用P 表示为

召回率（recall）可用R 表示为

F1 分数（F1-score）可用F1表示为

式中，TP表示分类正确的正例数目（ture positive），FN表示分类错误的负例数目（false negative），FP表示分类错误的正例数目（false positive），TN表示分类正确的反例数目（true negative）.

从表1 来看，定量分析同先前可视化得到的结果一致，原始图像以及LBP 特征图像的分级测定精度很低，而SURF 与GLCM 特征在分级测定中表现良好.原始图像与LBP 图像对细粒度颗粒图像的分类效果很差，当粒度相近时(0.9∼3.0 mm、3.0∼5.0 mm)F1均小于0.4.进一步分析可知，原始图像的全局像素点特征为二维像素点的像素值与排列信息，而这两者很难表征粒度信息.LBP 图像获取全局纹理信息虽然突出了边缘与纹理特征，但细粒度矿石的粒度信息不仅包括边缘纹理等信息还有一些统计特征，所以LBP 图像分类精确度反而比原始图像下降了37%.原始图像与LBP 图像的信息量虽然多，但难以表征细粒度矿石的粒度特征.SURF 算法通过提取矿石图像中的角点信息来描述粒度，粗粒度矿石的角点主要由矿粒边缘组成，数量少而清晰；细粒度矿石的角点主要是由矿粒表面的反射点组成，数量多而模糊.

表1 4 种算法的定量测试结果Table 1 Quantitative test results by four algorithms

GLCM 算法选取了从不同层面和角度描述纹理的特征值，在GLCM 上进行二次提取，可以在分类前清晰地描述图像的局部和全局纹理特征，多层次反映细粒度信息.虽然SURF 算法与自适应GLCM 算法都可以在一定程度上区分细粒度矿石颗粒的粒径大小，但后者在0∼0.9 mm、0.9∼3.0 mm 这种细小的矿石分类测定上更精确，且测定精度不会随着粒度的变小而下降.从平均水平来看，自适应GLCM 算法的精确度和召回率分别为92.37%与91.34%，F1为0.93，均优于其他算法.

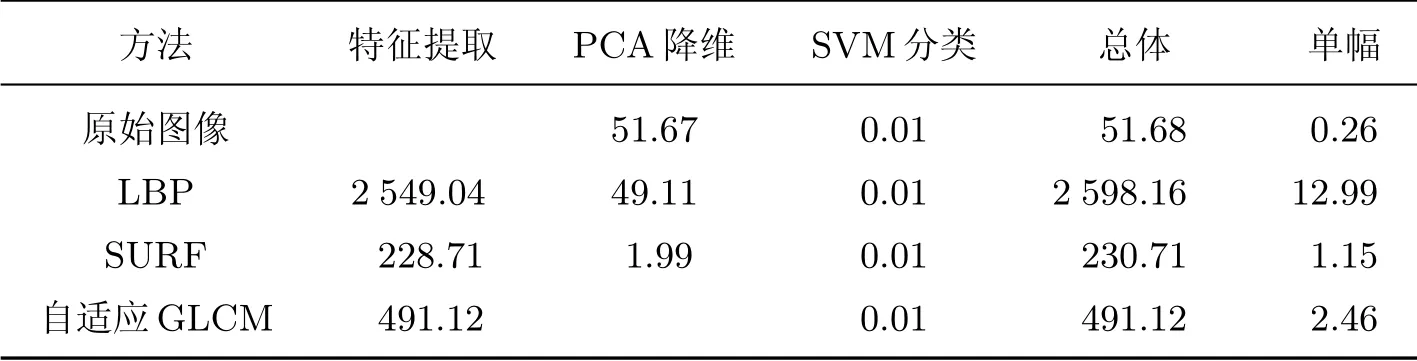
表2 不同算法在测试集上的计算时长Table 2 Calculation time on test set by different algorithmss

由表2 给出的计算时长可以知道，测定时间主要集中在特征提取方面.对于像素大小为1 500×2 000 的矿石图像，SURF 算法和自适应GLCM 算法均有不错的时效性.由于自适应GLCM 需要计算不同生成距离和灰度压缩等级情况下的特征值，在测定时间上略多于SURF 算法，但每幅图像的计算所用时间小于2.5 s，基本满足了实时检测的要求.

4 结 语

针对细粒度矿石分级测定时精度不足的问题，本文提出一种基于深度图像分析的细粒度矿石分级测定方法.该方法在传统GLCM 基础上，通过最大线性离散度优化算法改进点对生成距离和灰度压缩等级的选取过程，实现对矿石粒度信息的自适应提取；然后构建RBF-SVM 分类模型，并使用网格搜索与交叉验证方法优化核函数参数，实现细粒度矿石的准确分级测定.实验结果表明，本文方法对粒度在0∼7.0 mm 区间内的煤矿颗粒分级测定准确率可达92%以上，并且测定精度不会随着粒度下降而降低，能较好地适用于细粒度矿石分级测定.然而，该算法在时效性和光照鲁棒性方面还有待提高，这也将成为下一步研究的重点.