基于相位敏感光时域反射技术的导线舞动状态监测

郝伟博， 赵衍双， 李卓枢， 谢 凯， 邢 键，张建中， 苑立波

1.东北林业大学机电工程学院，哈尔滨150040

2.国网河南省电力科学研究院输电线路舞动防治技术实验室，郑州450000

3.哈尔滨工程大学纤维集成光学教育部重点实验室，哈尔滨150001

输电线路作为电网系统中的重要设施，其稳定性是确保电网安全运行的重中之重.然而，大风、覆冰等极端天气状况极易引发输电线路的舞动，严重时引起输电线路断裂以及输电杆塔倒塌等线路故障，导致供电系统停运而出现大面积停电现象，对社会造成极大的经济损失[1-2].鉴于此，本文建立一种新型的输电线路监测系统，能立刻检测出输电线路故障点并进行排查检修以提高电力系统的安全性、实时性、可靠性，这对于提高中国电网的安全性具有重要的理论和工程意义.

在1955年至今的半个多世纪里，中国发生了上千起电路系统故障，造成供电系统故障的主要原因是雨雪冰冻天气下输电导线发生覆冰和舞动灾害[3].其中，覆冰灾害引起的中国高压输电设备损坏达1 000 多起，35 kV 及以上的输电网发生的覆冰灾害高达87 起[4].随着中国电力设备的不断发展，覆冰、舞动灾害的发生频率也随之提高[5]，从2000年到2010年舞动引发的事故增至740 余例[6].仅以河南地区2003年为例，因导线舞动而造成的线路故障波及范围高达13 个地级市，在河南南部、东部地区造成10 kV 中压线路198 条、110 kV 及以上高压线路32条跳闸[7].因此，如何有效监测输电线路，提前预警供电系统故障已经成为世界各国维护电网安全稳定的首要工作[8]，为此各国进行了大量实验研究，也取得了一些行之有效且可供借鉴的经验[9].

自从Taylor 等人提出相位敏感光时域反射（phase-sensitive optical time-domain reflectometer, Φ-OTDR）以来[10]，该技术得到了不断发展[11]，传感距离和空间分辨率不断提高[12].Φ-OTDR 与传统OTDR 最大的不同在于Φ-OTDR 采用了具有窄线宽和低频率漂移特性的相干光源[13]，极大地提高了空间分辨率和振动强度分辨率[14].因为采用了先进的解调算法，所以Φ-OTDR 具有测量信噪比和准确率更高[15]、传感距离更长、实时性更好等优势，非常适合输电线路振动的监测[16].此外，Φ-OTDR 应用于输电线路的监测，可使单根光纤同时监测输电线路的振动、温度、应变等多种参量，从而减少输电系统不必要的设备，减轻输电线路不必要的重量，实现输电线路减负及运维管理简便的目的，大大增强电网感知的深度和广度，提升电网交互性、自动化和信息化[17].因此，本文利用舞动试验机系统测试不同激振频率下OPPC 的振动状态，通过对比激振频率和Φ-OTDR 测量信号，为Φ-OTDR 系统应用于输电线路的舞动监测提供实验基础.

1 试验系统组成

1.1 Φ-OTDR 系统

Φ-OTDR 系统是利用散射光的相干性设计出的相位敏感型光时域反射系统.光纤本身既是传输媒质又是感知元件，即光纤上任意一点都是传感单元，是一种真正意义上的全分布式光纤传感器.当光缆某位置发生振动时，该位置的光纤发生形变，从而改变该处折射率，最终导致该处光的相位发生改变.因此，返回的发生干涉的瑞利后向散射光光强会因相位的改变而发生改变.通过与未发生振动检测到的信号进行比较，最终找出光强变化的时间对应振动的确切位置.基于瑞利后向散射的Φ-OTDR 原理如图1 所示.

窄线宽激光器发出的激光，经过声光调制器（acousto-optic modulator, AOM）的脉冲，调制成重复频率为f、脉宽为W 的脉冲序列，由光功率放大器放大后经过环形器注入传感光纤.当前向脉冲光遍历传感光纤时，后向瑞利散射光逆着光传播方向经环形器进入光纤迈克尔逊干涉仪.经过干涉仪的干涉调制，干涉信号进入3×3 耦合器，由光电探测器探测光强以及数据采集卡采集数据后，根据相应的解调算法解调出传感光纤处的振动信息.

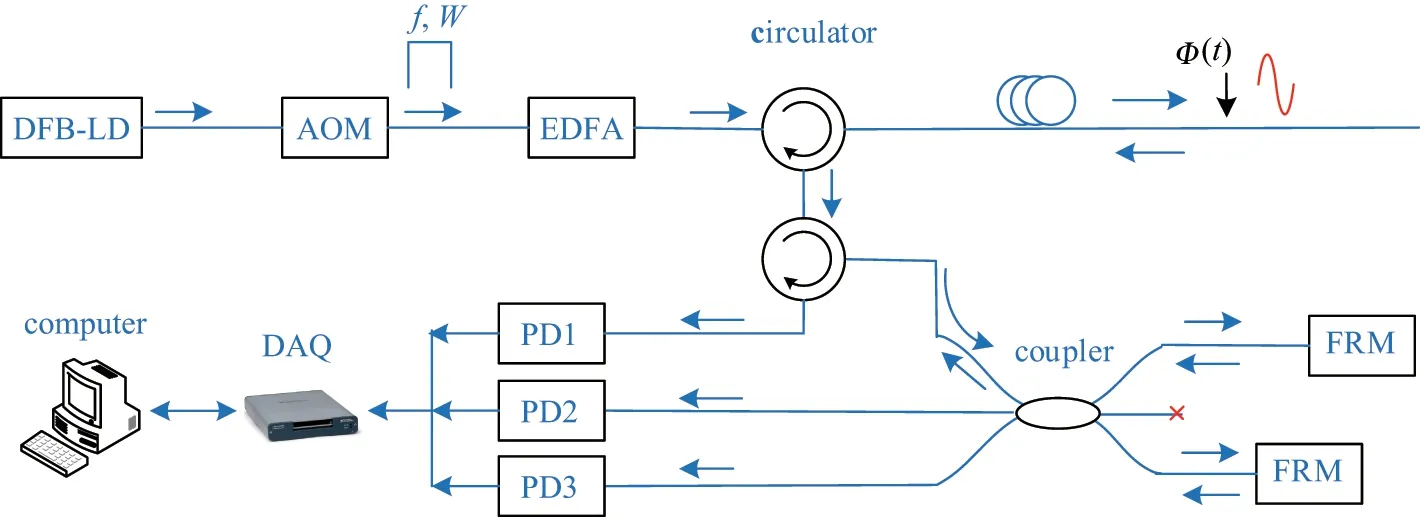
图1 Φ-OTDR 系统原理Figure 1 Principle of Φ-OTDR system

本次试验搭建的Φ-OTDR 系统性能指标如表1 所示.

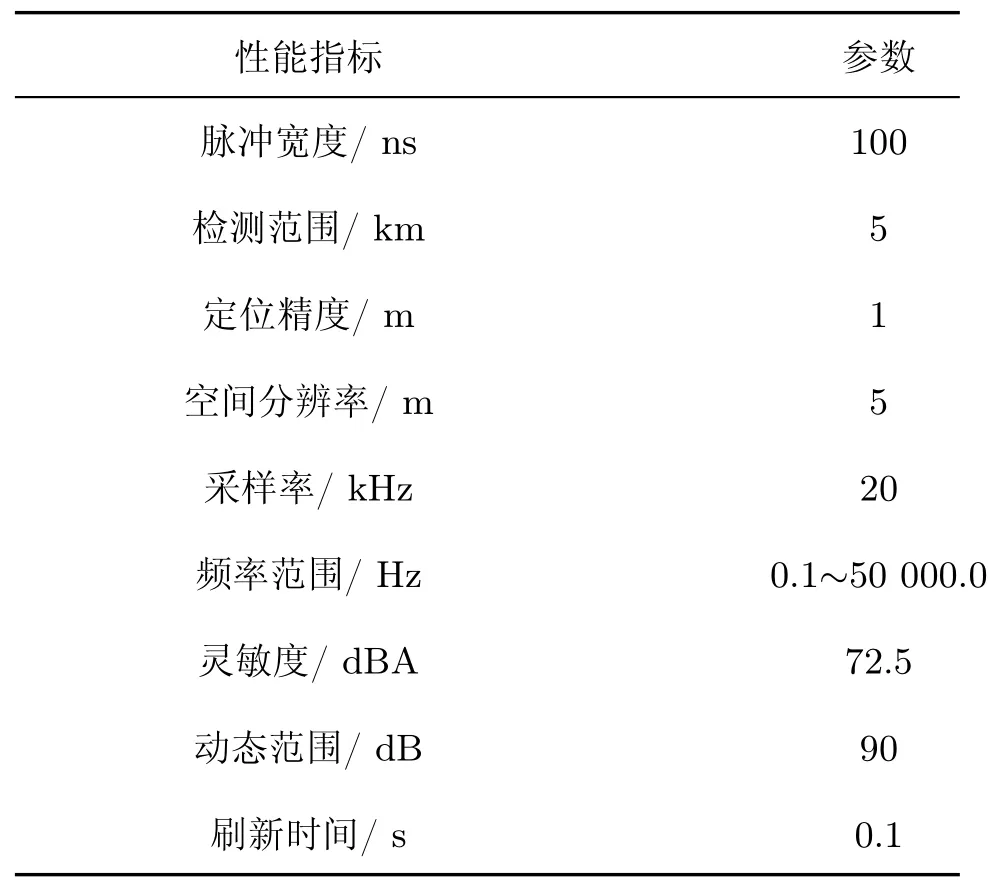
表1 Φ-OTDR 系统性能指标Table 1 Performance of Φ-OTDR system

1.2 舞动试验机系统

舞动试验机实物如图2 中的(a)所示，各组成部分位置分布如图2 中的(b)所示.悬挂点A 与B 的间距为61 m，激振器位于两悬挂点之间，与悬挂点A 和B 的距离分别为55.5 m 和5.5 m；光纤复合相线(optical phase conductor, OPPC)两端由预绞丝固定到悬挂点上，其中一端悬挂点A 的位置固定，另外一端悬挂点B 与耐张拉力机连接，两悬挂点之间的OPPC 长度约为61 m；利用耐张拉力机可以调整两悬挂点之间OPPC 的拉力，最大拉力可达105N；OPPC 与激振器连接，并由激振器施加不同频率的激振信号.

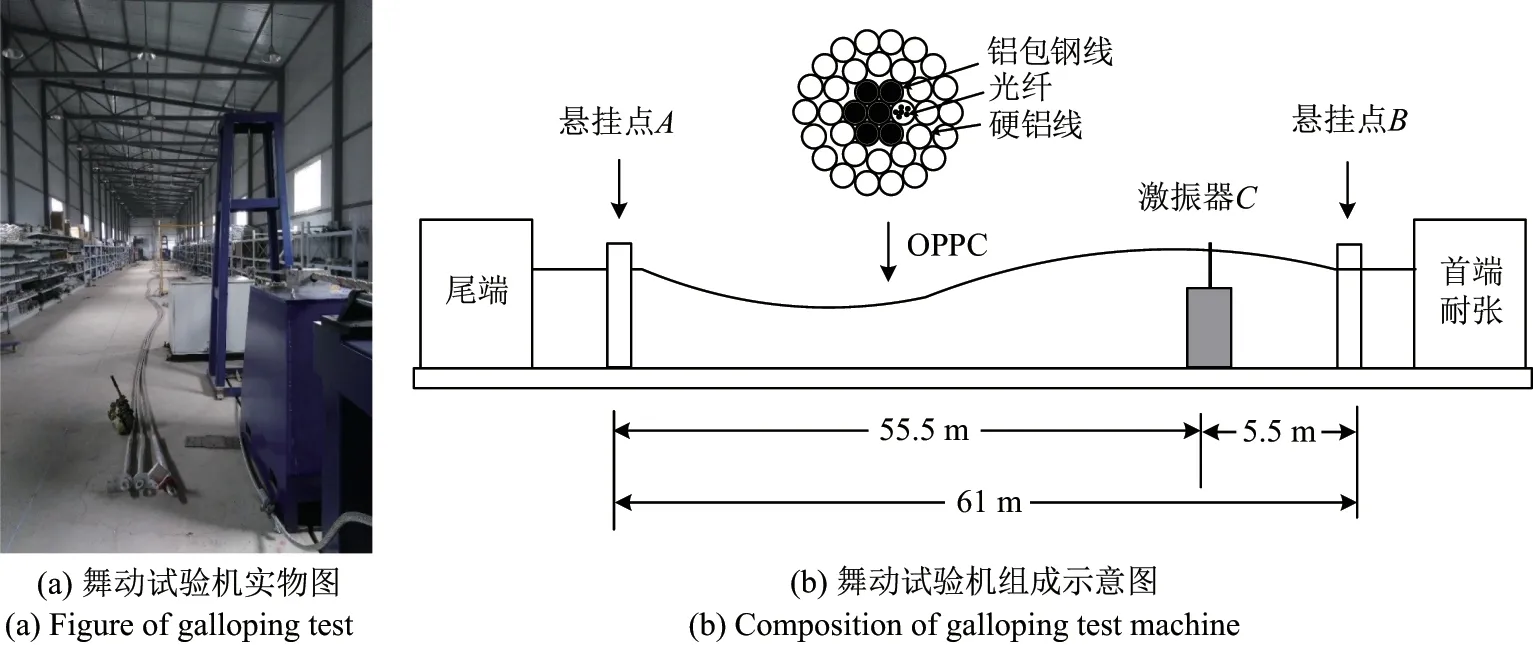
图2 舞动试验机Figure 2 Galloping test machine

悬挂点A、悬挂点B、耐张拉力机、激振器如图3 所示.

图3 舞动试验机各部分结构Figure 3 Structures of galloping test machine

试验中采用的OPPC 型号为OPPC-24B1-400/50，其外观和尺寸与常规LGJ-400/50 导线一致，内含24 根单模光纤.在舞动试验机尾端将OPPC 末端任意两根光纤熔接，并在舞动试验机首端处接入Φ-OTDR 系统.

2 舞动试验机OPPC应变仿真分析

如图4 所示，当激振器对OPPC 施加不同频率的激振时，OPPC 不同位置发生的应变变化可采用Comsol Multiphysics 有限元仿真软件进行模拟分析.OPPC 简化为铝线、填充物的两层结构.OPPC 直径设为36 mm，密度设为3 346 kg/m3，杨氏模量设为6.8×1010Pa，泊松比设为0.29；填充部分直径设为6 mm，密度设为2 540 kg/m3，杨氏模量设为7×109Pa，泊松比设为0.17.两悬挂点固定，其间距为6.6 m，激振器就位于两悬挂点之间.

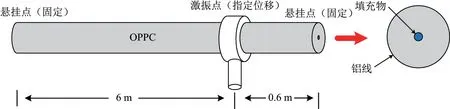
图4 OPPC 有限元方法的仿真模型Figure 4 Simulation model of OPPC by finite element method

在激振点位置施加幅值为0.5 m、频率为0.8 Hz 的激振，幅值随时间的变化为0.5cos(1.6πt)，经仿真得到OPPC 在10 s 时刻的应变和变形如图5 所示.

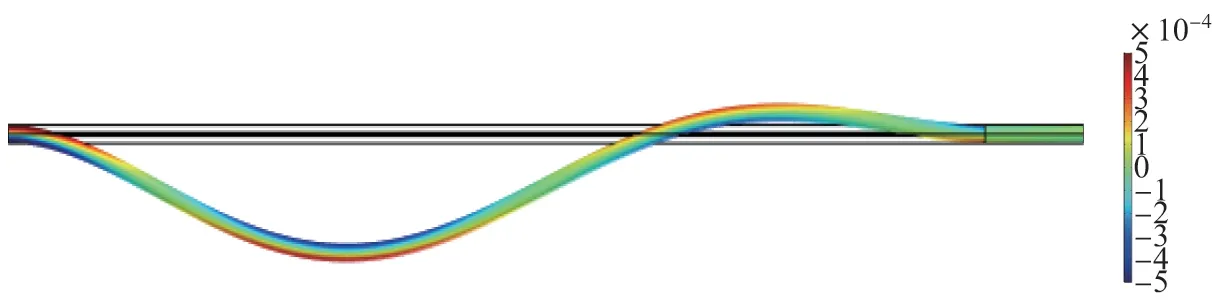
图5 OPPC 应变和变形的仿真结果Figure 5 Simulation results of strain and deformation of OPPC

提取OPPC 所有位置的应变在10 s 内随时间的变化如图6 中的(a)所示，激振器和悬挂点位置的应变幅值变化明显大于它们各自附近位置的应变幅值变化，这是由两个位置点的应力集中造成的.经傅里叶变换得到频域信号如图6 中的(b)所示，频域信号中出现对应激振频率0.8 Hz 的频率峰值信号.光纤位于填充物中心且相对于填充物较细，因此认为填充物中心的应变为光纤的应变.提取填充物中心位置的应变变化如图6 中的(c)和(d)所示，各个位置的OPPC 外表面应变均传递到填充物中心，可见应变衰减一致，因此光纤的应变可以充分反映OPPC 外表面的应变变化.

3 舞动模拟试验及测试结果分析

利用激振器对OPPC 施加不同的激振频率，模拟OPPC 覆冰后在风力作用下的舞动状态.当舞动试验机处于稳定状态即激振器未对OPPC 施加激振信号时，测试60 s 内的OPPC信号，测得时域信号后进行傅里叶变换，得到频域信号如图7 所示.OPPC 位于180∼270 m以及290∼380 m 位置.图7 中的(a)仅画出0∼1 s 内的时域信号.

由三维时域信号图7 中的(a)可以看出：当OPPC 处于稳定状态时，时域信号幅值较小且变化不大，说明OPPC 各个位置的应变较稳定.由三维频域信号图7 中的(b)可以看出：频域信号峰值较高的位置集中于0.1 Hz 以下，说明OPPC 中光纤应变变化缓慢，可能由外界环境缓变因素如温度波动所引起.

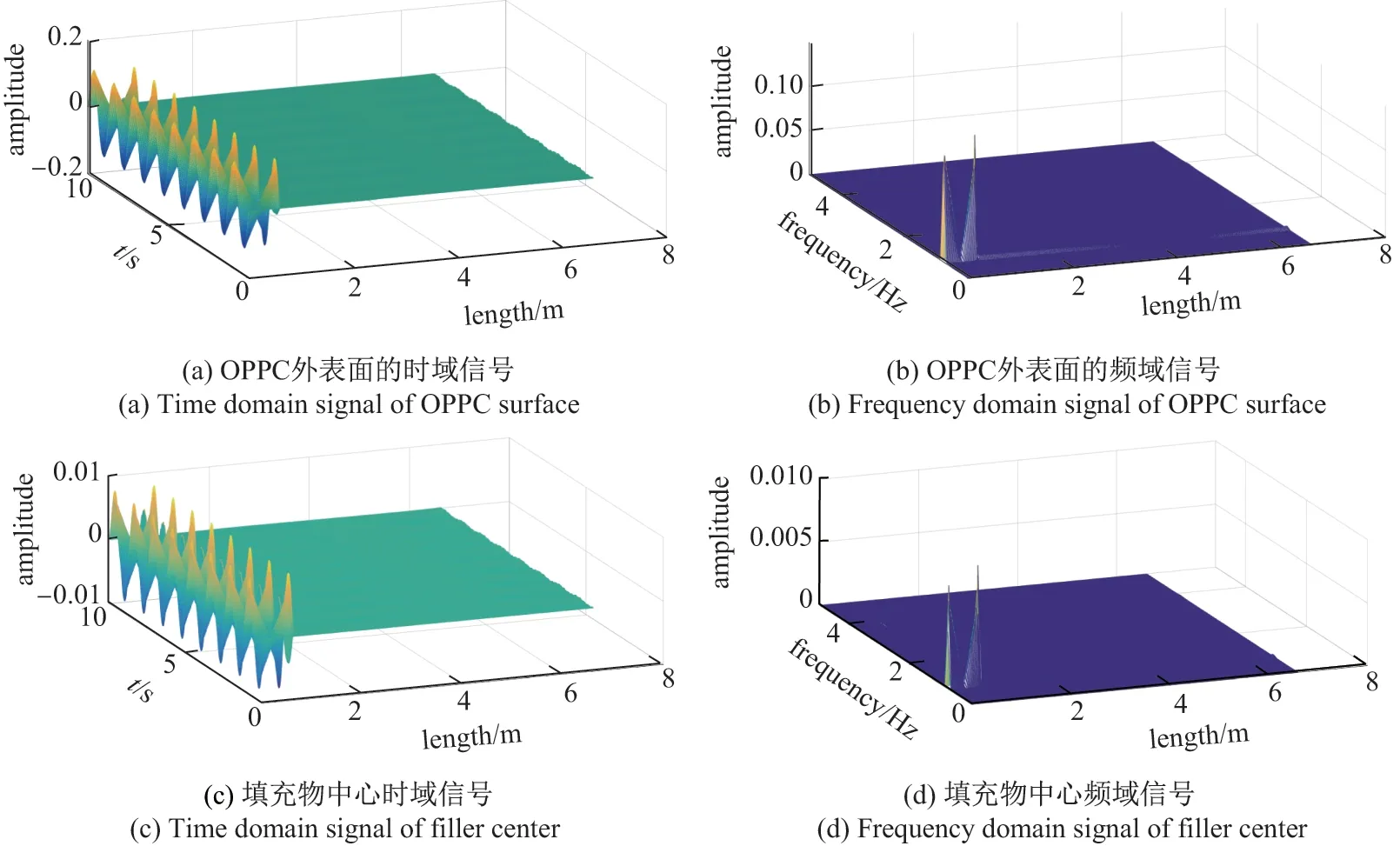
图6 激振频率为0.8 Hz 时OPPC 外表面和填充物中心的应变变化Figure 6 Strain changes of OPPC surface and filler center with 0.8 Hz excitation frequency

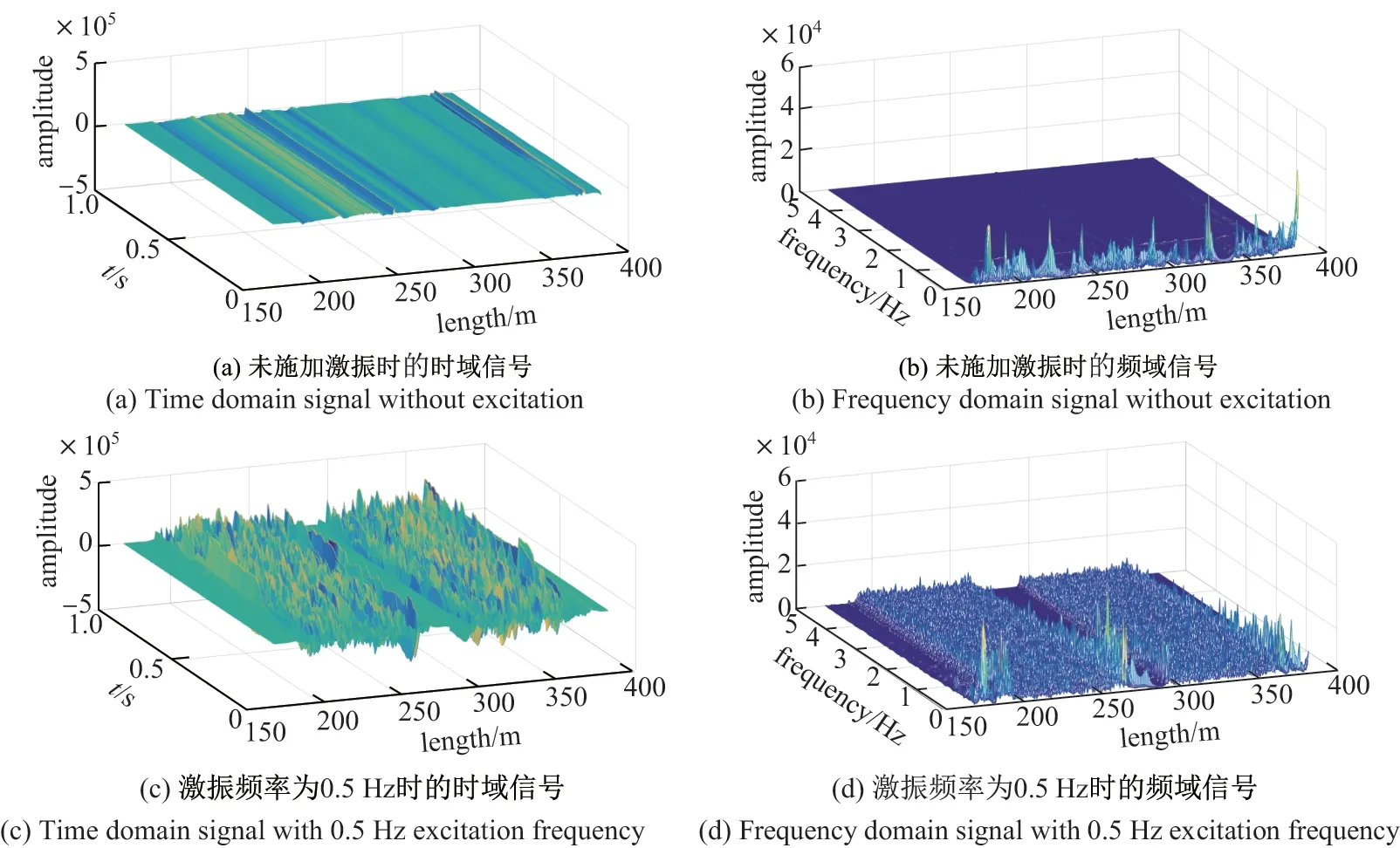
图7 是否施加激振时由Φ-OTDR 测得的信号Figure 7 Signal measured by Φ-OTDR with and without excitation frequency

控制激振器对OPPC 施加频率为0.5 Hz 的激振信号，测得时域信号并进行傅里叶变换,得到频域信号如图7 中的(c)和(d)所示.因为OPPC 中的光纤在尾端处连接，所以测量信号关于光纤长度280 m 处为基本对称的两部分，其差异性是由光纤在OPPC 中的位置不同以及光纤内光的偏振态变化所引起的.

与未施加激振时相比，施加激振后的时域信号幅值显著增大，OPPC 应变变化剧烈，出现了OPPC 悬挂点频率信号强而其他位置频率信号弱的现象.在OPPC 悬挂点位置出现与激振频率值相同的较高的频率峰值，同时在悬挂点A 和B 之间的OPPC 位置出现与激振频率一致即0.5 Hz 的频率峰值.

随着所施加的激振频率的升高，OPPC 舞动幅值总体上逐渐增大，最大出现在共振频率1 Hz 附近.控制激振器对OPPC 施加频率为1 Hz 的激振信号，测得时域信号并对其进行傅里叶变换，得到频域信号如图8 所示.在OPPC 各个位置的振动中，出现与施加激振频率相等的1 Hz频率峰值.与图7 中的(c)和(d)施加0.5 Hz 激振的信号相比，激振对应的频率在OPPC各个位置明显高于其他频率，而OPPC 中的其他振动频率被显著抑制.

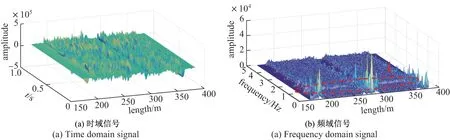
图8 施加频率为1 Hz 的激振时由Φ-OTDR 测得的信号Figure 8 Signal measured by Φ-OTDR with 1 Hz excitation frequency

将仿真结果图6 与施加激振的实验结果图7 和8 进行对比，悬挂点位置的应变变化高于各悬挂点附近的应变变化.在仿真图中仅出现与施加激振频率相对应的频率峰，而在实验结果中出现多个杂散频率峰，造成这种差异的原因如下：激振器施加的频率不是绝对单一频率，而是混杂有其他频率；施加激振后，整个舞动试验机结构产生其他频率，一旦传递到OPPC上，就会混杂到测量信号中.

取OPPC 所有位置点与激振频率一致的频率信号强度，如图9 所示.在OPPC 悬挂点A、B 和激振器C 的位置附近，激振频率值对应的频率信号强度高于其他位置的信号强度，这是因为悬挂点和激振器位置附近出现应力集中，导致应变变化剧烈.在OPPC 除悬挂点A、B和激振器C 外的其他位置，当激振频率较低时，频率信号强度在光纤长度方向上抖动剧烈.

取图9 中OPPC 除悬挂点A、B 和激振器C 外其他位置与激振频率一致的频率信号强度总体值，如图中红色线所示，得到强度总体值随激振频率的变化如图10 所示.随着激振频率的不断升高，激振频率值对应的频率信号的强度总体上呈上升趋势.当激振频率为1.0 Hz 时,信号强度达到最大，其值为1.06×104；当激振频率继续增大至1.1 Hz 时，激振频率值对应的频率信号的强度迅速减小至0.3×104.当激振频率较低时，OPPC 中被激起的频率较多；当激振频率越来越高并接近固有频率1.0 Hz 时，其他频率的信号被抑制；当激振频率为1.1 Hz 时，激振远离固有频率，信号强度变低.

4 结 语

本文利用Φ-OTDR 系统，通过激振器对舞动试验机上的OPPC 施加不同的激振频率，提取不同振动状态下Φ-OTDR 系统测量信号的特征.对于同一激振频率，导线悬挂点和施力点等应力集中位置采集到的信号明显高于整根导线其他位置的信号；对于不同的激振频率，当接近1.0 Hz 固有频率时，整根导线信号明显大于其他激振频率下的信号.实验结果证明了以Φ-OTDR 系统监测输电线路导线舞动信息的可行性，这对于利用Φ-OTDR 技术实现真实输电线路舞动状态监测奠定了实验基础.

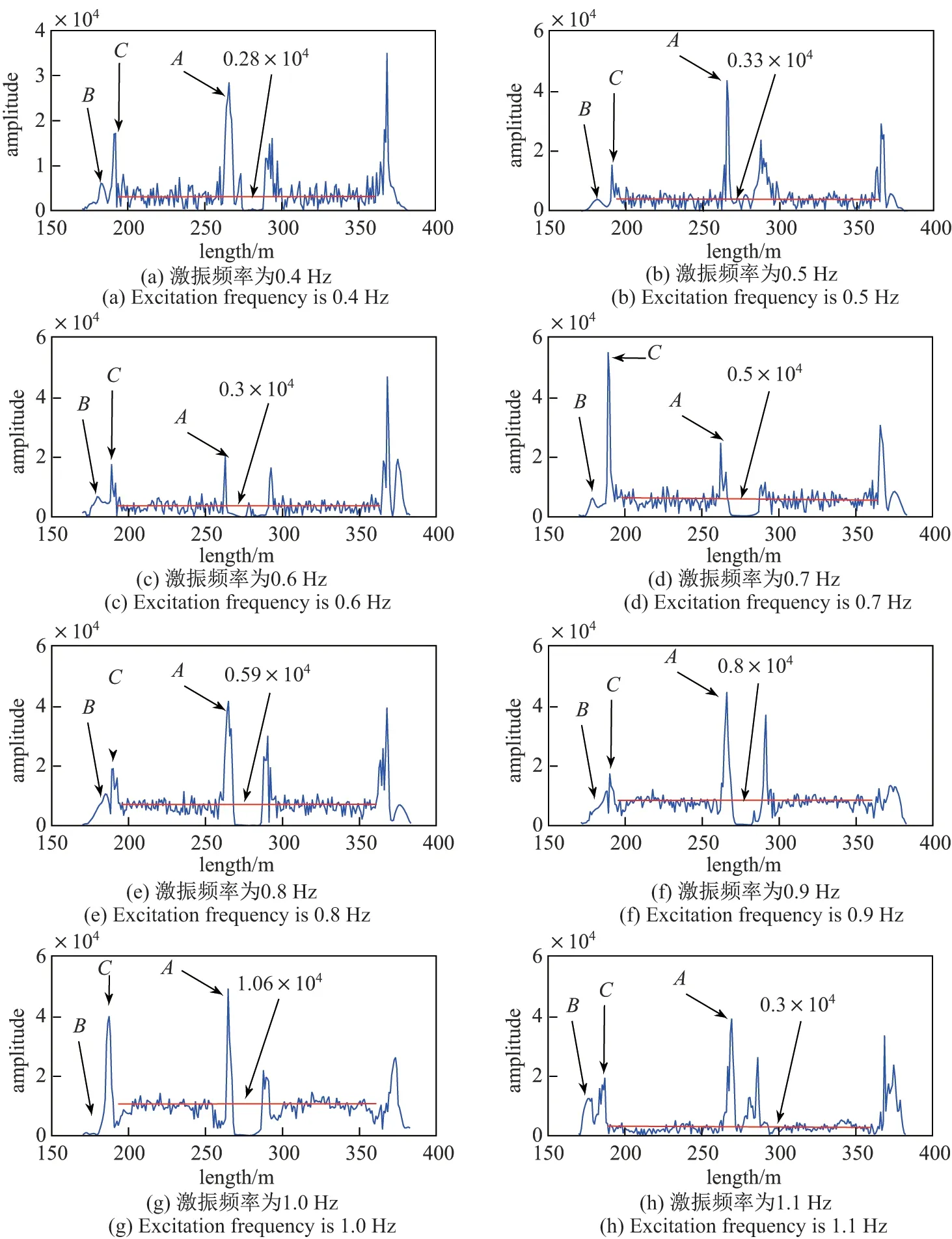
图9 施加不同频率的激振时由Φ-OTDR 测得的相应频率的信号Figure 9 Signal of corresponding frequency measured by Φ-DTDR when excitation of different frequencies is applied

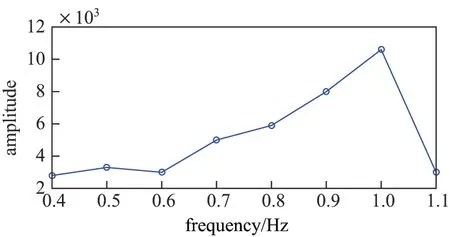
图10 激振频率与相应频率的信号强度关系Figure 10 Relationship between excitation frequency and signal amplitude of corresponding frequency