基于LCL 滤波器的复合控制策略

玄兆燕， 贾万泳， 陈学斌， 景会成， 赵 欣， 马振宇

1.华北理工大学机械工程学院，河北唐山063210

2.华北理工大学理学院，河北唐山063210

3.华北理工大学电气工程学院，河北唐山063210

4.唐山市拓又达科技有限公司，河北唐山063020

现今，能源枯竭和环境污染问题日益严重，以太阳能、风能、地热能等可再生能源的开发和利用成为研究热点[1].分布式发电系统的加入进一步促进了可再生能源的利用，并通过逆变器接入电网，但非线性元件的使用产生了大量谐波[2].LCL 滤波器因其体积小、成本低、滤波效果好等优点而得以广泛应用.但因为LCL 滤波器是三阶系统，所以存在谐振尖峰及相位跳变，导致系统不稳定.

为保证系统稳定运行，并网逆变器通常采用比例积分(proportional-integral, PI)控制、比例谐振(proportional resonance, PR)控制、重复控制、准比例谐振(quasi-proportional resonance,QPR)控制、无差拍控制等策略.PI 控制结构简单，动态响应速度快，稳态精度低；PR 控制利用基频处的谐振得到基频处的增益，能完全消除稳态误差，但无法消除非基频处的谐波；QPR 控制既保留了PR 控制优点又解决了PR 控制非基频处谐波无法消除的问题；重复控制动态响应慢，稳态精度高；无差拍控制精度高，动态响应好却过于依赖精确电路模型.

随着用电要求的提高，单一的控制策略越来越不能满足高精度的并网标准，于是将多种控制策略进行整合，这样有利于优势互补，达到了最佳的并网效果.文献[3-5]将PI 与重复控制并联或者串联成复合控制，提高了动态性能和稳态精度.然而，PI和重复控制之间存在控制耦合，导致动态时并网电流发生部分畸变.文献[6-8]提出PI+QPR 解耦控制，由PI 控制器负责系统稳定，由QPR 负责降低系统谐波干扰，虽然提高了动态性能，但不可避免地产生稳态误差.文献[9-10]将QPR+重复控制用于电压控制，降低了冲击性负载对电压的扰动，但对扰动频繁的系统调节速度较慢.基于以上分析，本文提出将重复控制与QPR 并联再串联PI 的复合控制策略，既保证了动态性能，又提高了稳态精度，还减少了控制耦合.

1 单相并网逆变器拓扑结构

图1 为单相并网逆变器主拓扑结构，逆变器直流侧输入电压为400 V，交流侧通过LCL 滤波器滤波后并入电网.其中：L1和L2分别为逆变侧电感和电网侧电感；C 为滤波电容，可以分流谐波电流；RC为电容串联电阻；r 为滤波器电感与系统阻尼的综合等效电阻[11]；Ug为电网电压.

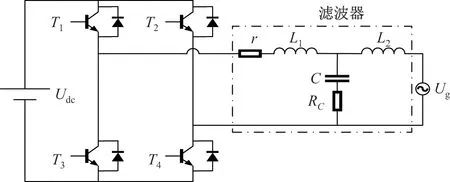
图1 并网逆变器的主拓扑结构Figure 1 Main topology structure of grid-connected inverter

由基尔霍夫电流和电压定律可得滤波器传递函数为

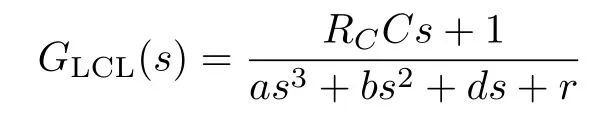
式中

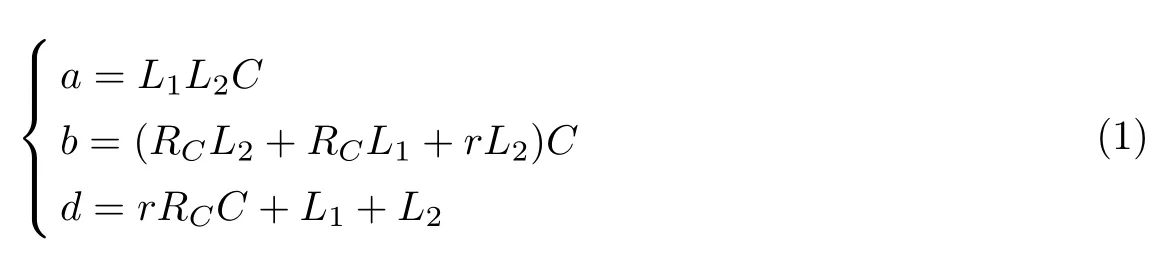
当忽略LCL 等效电阻和电网内阻时，被控对象幅频曲线有无限高的谐振峰值，而考虑电阻时的谐振明显降低[12]，其被控对象的伯德图见图2.

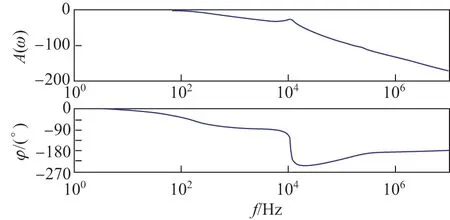
图2 被控对象的伯德图Figure 2 Bode diagram of controlled object

由图2 可知：在高频段幅值迅速衰减，抑制了进网电流中由开关频率引起的高频谐波，但在低频段及谐振频率处出现了相位剧变和幅值干扰的现象，导致系统不稳定，以致增加了控制难度[13].

在数字控制系统中，当正弦脉宽调制(sinusoidal pulse width modulation, SPWM)信号发生变化时，逆变器输出电压需延时到下一个周期才发生变化.因此，逆变器可看成是一个滞后环节[14]，其逆变传递函数为

式中，KPWM为直流输入到交流输出的传递函数.现将G1进行泰勒展开，所得传递函数的分式形式为

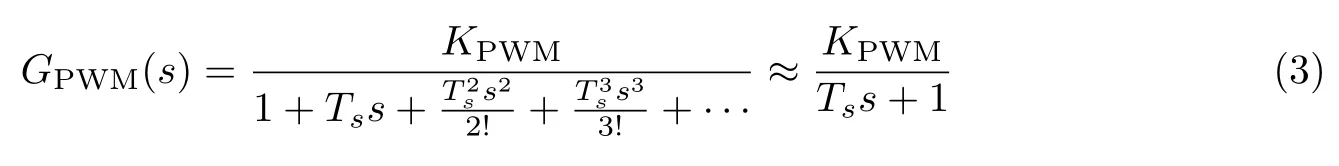
式中，Ts为逆变桥开关周期.现选择开关频率为10 kHz，此时Tss+1 ≈1，即逆变桥传递函数为KPWM.

2 控制器设计

2.1 PI 控制器设计

PI 控制器对截止频率以下的谐波都具有一定的抑制能力，通常可与电网电压前馈控制策略相结合以实现无静差跟踪，保证电网运行得安全稳定.

2.1.1 简化被控对象模型

定义等效被控对象模型[15]为

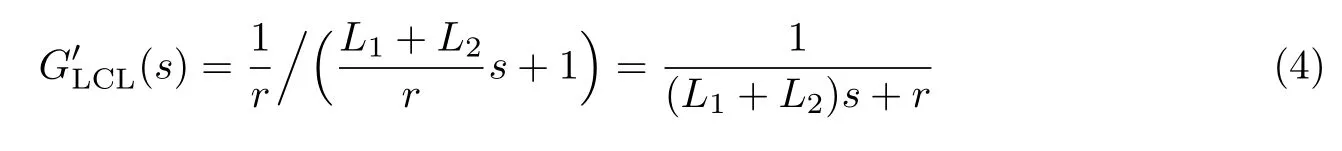
原传递函数与等效传递函数的伯德图如图3 所示.

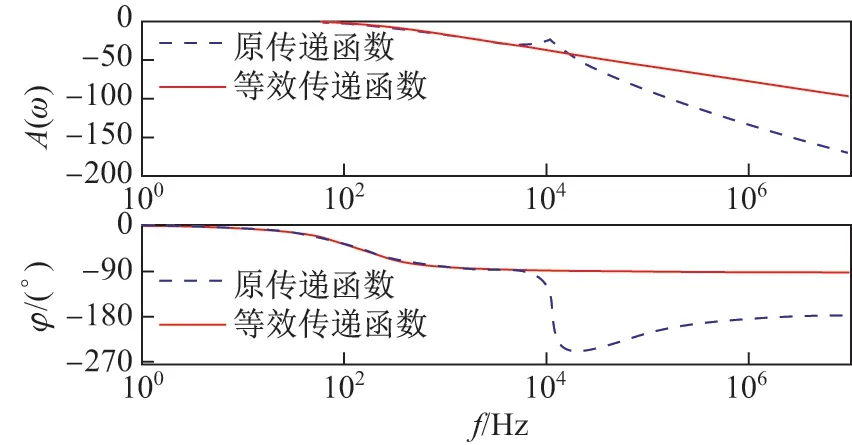
图3 传递函数对比图Figure 3 Comparison chart of transfer function

由图3 可知，被控对象伯德图与等效被控对象伯德图在低频段完全重合，故可用等效被控对象传递函数设计PI 控制器，以简化计算过程.

2.1.2 PI 控制器设计

PI 控制器的基本形式为

式中，Ti表示积分时间.系统用PI 调节时的开环传递函数为

为保证稳态效应，消除低频段相移和谐波干扰，式(6)在谐振频率处的增益为1，由此可以得到

式中，ωres为滤波器谐振频率.取积分时间Ti=0.01，并将表1 中的数据代入可得KPI=0.372，则电流内环PI 调节器的计算公式为

2.2 重复控制器设计

根据控制理论可以将复合控制看成两个分控制的叠加.当突然加载或卸载时，参考电流与反馈电流之间的差值增大，但重复控制器由于相位滞后不能及时进行调整.在初始阶段，由PI 和QPR 调节输出的误差值，以便快速调整指令电流.随着指令电流的逐渐减小，PI 和QPR 控制器慢慢失去调节作用，转而由重复控制器取代，直至系统重新达到稳定[16].

2.2.1 重复控制器模型

重复控制器拥有良好的抑制基波与谐波扰动的能力，可以有效提高并网电流质量，其离散域内膜为

式中，N 为一基波周期内的采样点数，且N = fs/f0；Q(z)的取值与系统的收敛速度、收敛程度息息相关.对于理想重复控制系统，跟踪参考信号的频率范围应为无穷大，但实际上跟踪所有频率的信号是不可能实现的.因此，Q(z)应具备低通特性，抑制周期性干扰[17].当Q(z) = 1 时，系统对输入信号实现无静差跟踪，此时系统处于临界稳定状态.在通常情况下，以牺牲系统极小的跟踪精度来确保稳态裕度.综合以上分析，选取Q(z)=0.98.

2.2.2 补偿器设计

由图2 可知被控对象在谐振频率附近，相位滞后，幅值衰减.为使系统稳定，设计补偿器对其相位进行超前补偿，使其在低频段实现0 增益和0 相移.

因为电容值远远小于电感值与电阻值，所以被控对象传递函数近似为

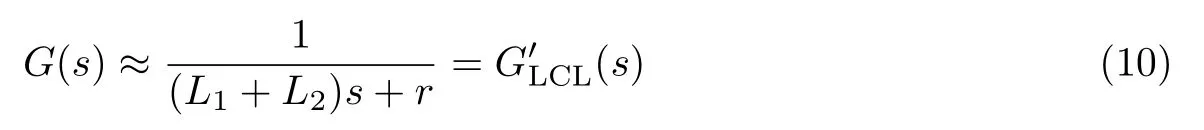
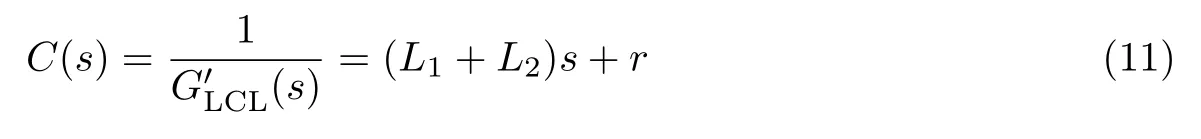
采用双线性变换法离散化得

2.2.3 陷波器设计

应用C(z)补偿前后的伯德图如图4 所示

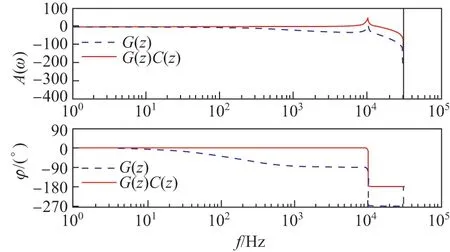
图4 应用C(z)补偿前后的伯德图Figure 4 Bode diagram by applying C(z) before and after compensation

由图4 可知，通过补偿器进行补偿只能保持低频段幅值和相位基本不变，但谐振处尖峰还未消除.现通过零相移陷波器来抑制尖峰的产生，这种方法可以在不影响其他频段幅值的情况下对特定频率的幅值进行迅速衰减，故不必进行相位补偿[18]，其传递函数基本形式为

式中，m 为陷波器阶数，影响陷波频率.在z 域中，z =ejwTs=ejθ，即

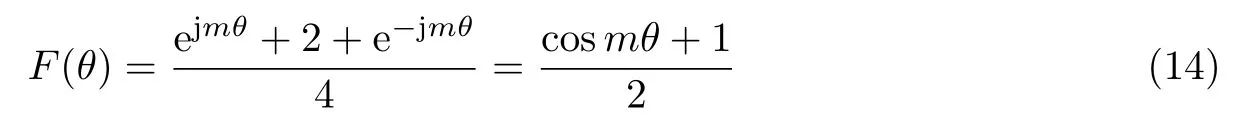
由式(14)可知，F(θ)有无限多个陷波频率.补偿时通常只补偿第1 个陷波频率，即在滤波器谐振频率ωres处，F(θ) = 0.已知θ = ωTs，代入式(14)可得代入参数可得m1=2.8，对m1取整后可得m1=3，则

由文献[12]可知，单一的陷波器不足以产生足够的高频衰减.文献[19]在消除陷波频率时又引入二阶滤波器对高频谐波进行衰减，其函数表达式为

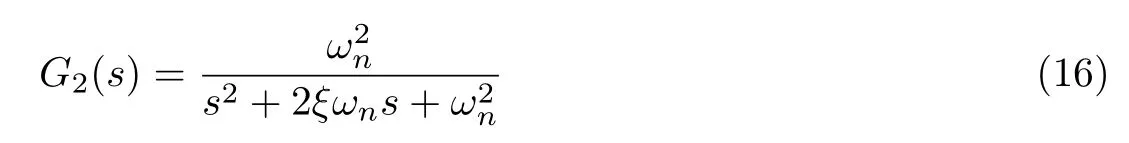
式中，取最佳阻尼比ξ =0.707，ωn为固有频率.

采用双线性离散化可得

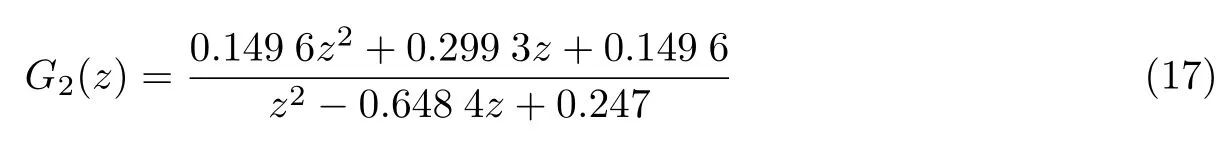
在此采用陷波器组的形式来消除谐振，衰减高频信号.选取m2=2, m3=4，则表达式为

令陷波器组为F(z)=F1(z)F2(z)F3(z)，图5 为不同补偿情况下的频率特性图

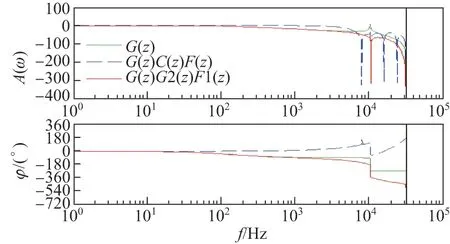
图5 被控对象与不同补偿器的频率特性Figure 5 Frequency characteristics of controlled objects and different compensators

由图5 可知，因为采用陷波器组的补偿，所以在低频段时系统更加稳定且在谐振频率及高频段幅值迅速衰减，有效抑制了谐波干扰.此外，陷波器组设计的灵活性更能对特定的高频谐波进行衰减，保证了系统的稳定性.

2.3 QPR 控制器设计

基于QPR 控制器良好的无静差跟踪特性，应用QPR 对PI 重复控制器进行补偿能提高系统的抗干扰能力，其传递函数为

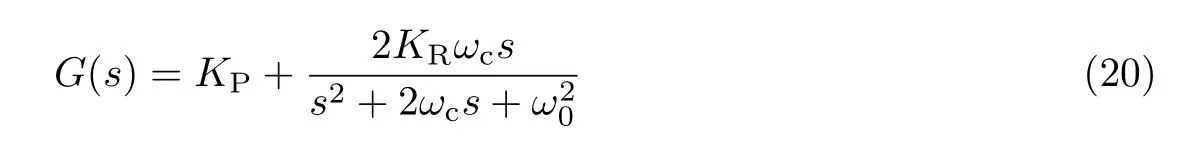
式中，KP综合考虑了系统抗干扰能力和系统震荡频率，此处选取KP= 7.KR与系统误差和谐波含量有关，为降低谐波含量，减小系统误差，选取KR= 400.ω0为基波频率，ωc为系统截止频率.

3 控制系统模型及稳定性分析

根据各控制器的特点，为保证更好的动态和稳态特性，先将QPR 与重复控制器并联，再与PI 控制器串联，其控制系统如图6 所示.

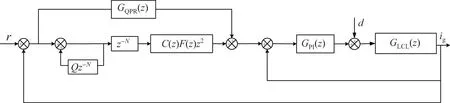
图6 系统控制策略Figure 6 Control strategy of system

当系统稳定运行时，反馈电流与给定电流误差小，整个系统主要由重复控制器起作用，其传递函数为

式中

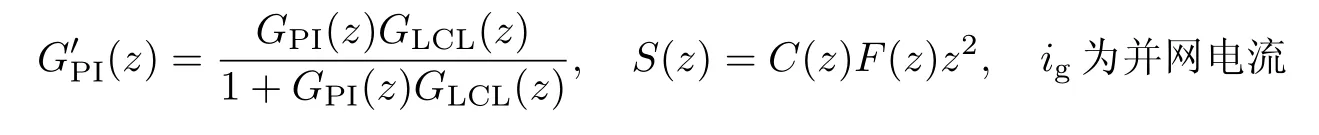
发生扰动时，反馈电流与给定参考电流之间误差突增.由于重复控制器存在相位延迟，此时PI 控制器和QPR 控制器迅速调节误差.经过一个基波周期后，重复控制器开始工作，调节反馈电流，精确跟踪给定电流，误差逐渐减小，致使PI 控制器输出减小，系统逐渐被重复控制器取代，直至系统稳定运行，其传递函数为

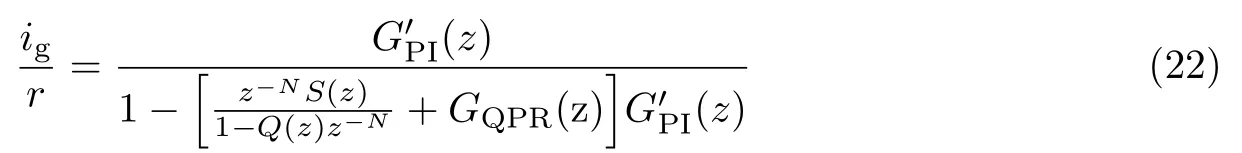
其复合控制传递函数为

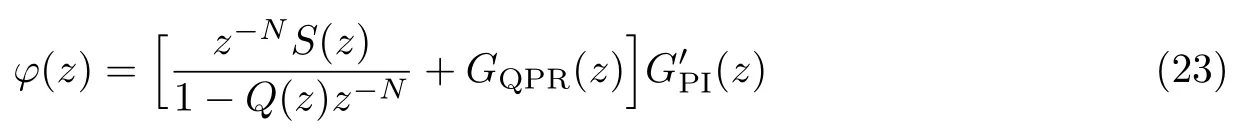
由开环系统传递函数可得其特征方程为

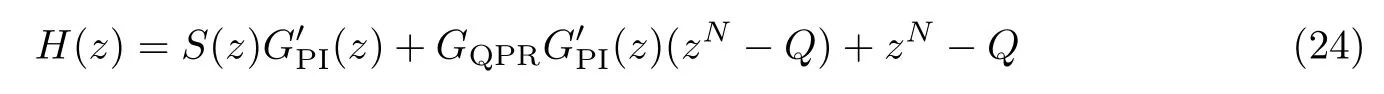
图7 给出了特征方程的根分布，从图中可以看出系统特征根均在单位圆内，因此采用串并联复合控制策略时系统具有良好的稳定性.

图7 特征方程根分布图Figure 7 Distribution map of feature equation root

4 仿真验证

为验证所提出的串并联复合控制策略的优越性，搭建了不同控制器的Matlab 仿真模型，其控制参数如表1 所示.

表1 逆变器系统参数Table 1 Parameters of inverter system

图8（a）和图9（a）分别给出了稳态控制时PI控制器、PI+重复控制器的电流波形，由局部放大图可以清楚地看出，图9（a）相较于图8（a）中的跟踪误差更小.在PI+重复控制中，随着控制时间的增加，电流跟踪误差越来越小，跟踪电流与给定电流基本重合.与单独采用PI控制器相比，输出电流更稳定，更可靠.

采用PI 控制时，输出的并网电流FFT 分析结果如图8（b）所示，从图中可以看出，电流有效值为15.42 A，存在0.13 A 的稳态误差，且衡量总谐波失真情况的THD 为0.51%；图9（b）给出了PI+重复控制的电流FFT 分析结果，电流有效值为15.43 A，存在0.12 A 的稳态误差，总谐波失真THD 为2.32%.

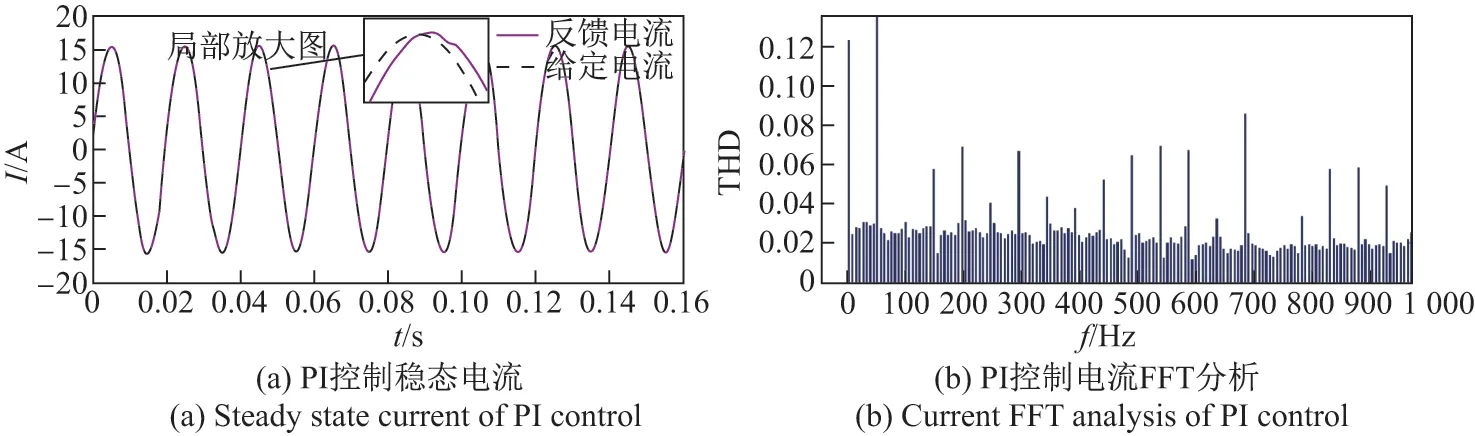
图8 PI 控制稳态电流分析Figure 8 Steady state current analysis of PI control

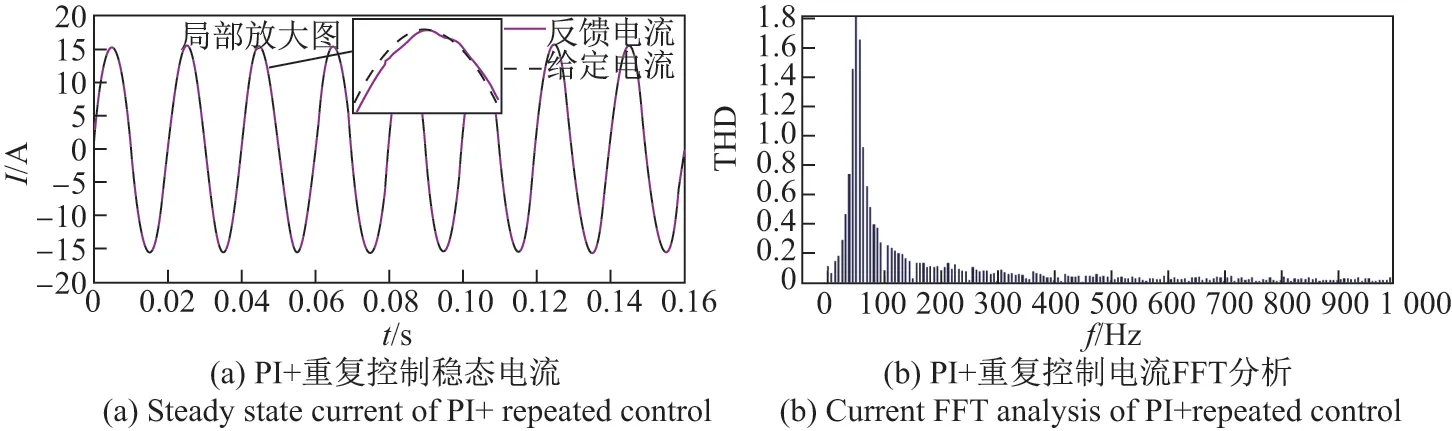
图9 PI+重复控制稳态电流分析Figure 9 Steady state current analysis of PI+repeated control

稳态时复合控制器电流波形如图10 所示，由图可知电流有效值为15.55 A，总谐波失真THD 为0.81%，且基频处谐波控制在0.15%以内，反馈电流跟踪给定电流的误差比PI 和PI+重复控制的误差更小，基本实现了零误差控制.在各个控制策略下，指令电流与反馈电流的实时误差如图11 所示，由图可知复合控制精度高，指令电流与反馈电流误差收敛在−0.5∼0.5 A 的极小范围内.

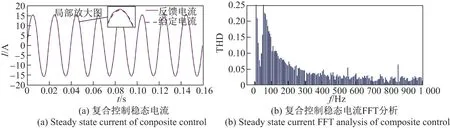
图10 复合控制稳态电流波形图Figure 10 Steady-state current waveform of composite control

图11 指令电流与反馈电流的误差Figure 11 Error of command current and feedback current

在不同控制策略下，稳态电流误差分析如表2 所示.%

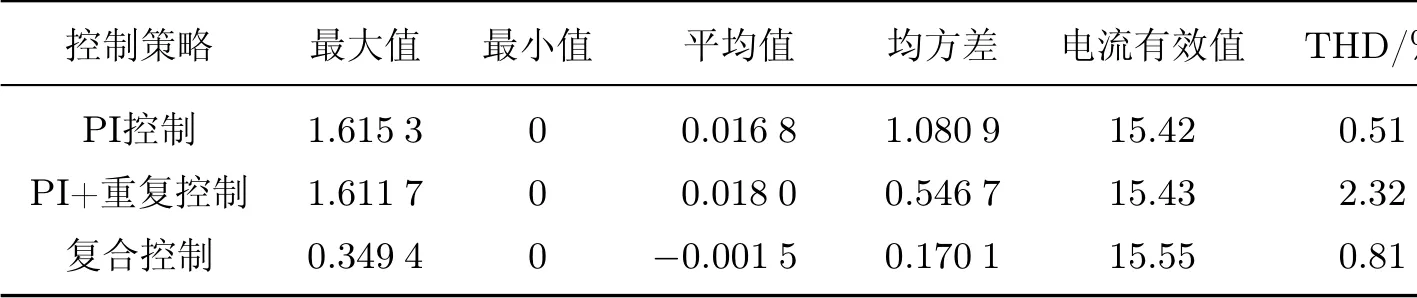
表2 在不同控制策略下的稳态电流误差分析Table 2 Steady-state current error analysis under different control strategies

在不同的控制策略下，电流THD 均小于国家标准的5%.在复合控制策略下，反馈电流与给定电流之间的误差最大值、最小值、均方差以及平均值的绝对值均小于PI 控制和PI+重复控制策略下的误差值，由此可知复合控制策略的稳态精度最高.由电流有效值可知，复合控制策略误差为0，基本实现了零稳态误差控制.

在不同的控制策略下，电压实时误差分析如表3 所示.由表3 的4 项指标可以看出，在复合控制策略下，电压波动较小，满足国家电网规定的±10%的误差标准.动非常明显，反馈电压与给定电压之间误差增大；采用复合串并联控制策略时，反馈电压实时跟踪指令电压，有利于公共电网的稳定运行.

表3 在不同控制策略下的动态电压误差分析Table 3 Dynamic voltage error analysis under different control strategies

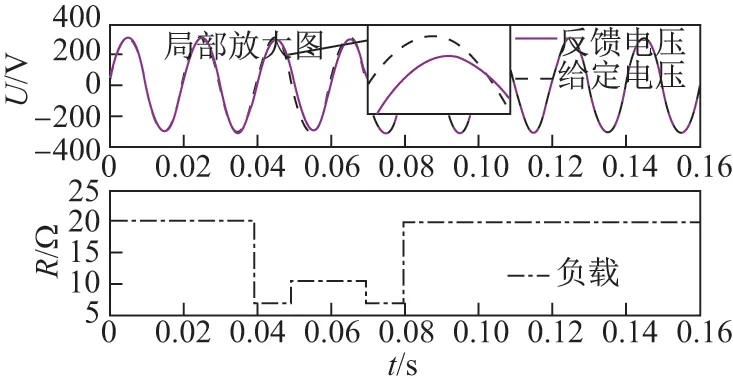
图12 PI+重复控制动态电压波形Figure 12 Dynamic voltage waveform of PI and repeated control

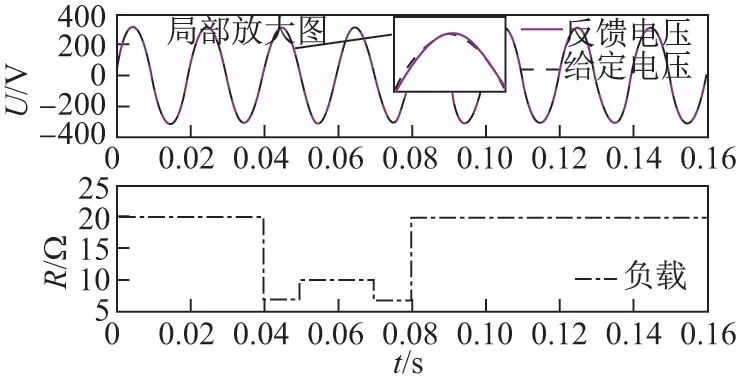
图13 复合控制动态电压波形Figure 13 Dynamic voltage waveform of composite control

5 结 语

串并联复合控制结构具有比PI更好的稳定性，比PI+重复控制更优的抗干扰能力，且输出电流误差更小.稳态时，重复控制可以降低稳态误差，提高系统的稳态精度；动态时，PI 控制可以迅速调节输出电流，使其快速跟踪给定电流；QPR 控制提高了系统的抗干扰能力，即使在负载的扰动情况下也能保证电网电压的稳定性，有利于实现大规模并网.