基于异或解密的标记视觉密码方案
徐梦琦, 吕东辉, 任艳丽,2,3
1.上海大学通信与信息工程学院,上海200444
2.上海先进通信与数据科学研究院,上海200444
3.上海交通大学可扩展计算与系统重点实验室,上海200240
随着信息技术的不断发展,互联网应用已成为生活当中不可或缺的重要角色.海量的数据信息需要通过互联网传输,因此数据信息分发中的安全性日益突出.在这些信息中,图像信息在信息交流中占有相当大的比例,可见其安全性更加重要.目前,图像加密是保护传输图像中数据和信息安全的方法之一,它是一种利用密码学保护图像数据的技术.当前比较成熟的技术有基于空间域的像素置乱、基于混沌的加密、基于变换域的加密等[1].这些技术均采用复杂的算法对信息进行加密和解密,显然在时间和计算资源方面产生浪费,因此迫切需要一种简单、计算量小且能达到应用需求的新算法.
视觉密码方案这一概念最初由Shamir 和Naor[2]提出,是一种简单又安全的密钥方案,具有恢复的简单性和一次一密的安全性.该方案将秘密图像编码成多个分享份,其中每个分享份均为噪声无意义图像,这样就不会泄露秘密图像信息;同时将生成的分享份分发给不同参与者,只有一定数量以上的分享份子集叠加才可以恢复秘密图像,而其他子集是无法恢复秘密图像的.在传统视觉密码方案中,最初将分享份复印在透明胶片上,通过叠加透明胶片能够可视地恢复秘密图像.这种方法操作简单,但存在像素扩展和设计加密矩阵等问题.
Kafri 等人于1987年首次提出(2, 2)随机网格方案[3],避免了设计加密矩阵等问题.文献[4]在此基础上将(2, 2)随机网格方案拓展到(k, n)的情况,即一幅秘密图像产生n 幅分享份,其中每幅分享份均为噪声无意义图像,只有将任意k 幅或大于k 幅分享份叠加才可以恢复秘密图像信息.文献[5]基于随机网格的方法提出了能够加密灰度图像的方案;随后文献[6]根据用户重要性的不同产生优先级不同的分享份,以防止秘密信息泄露.然而,在传统视觉密码方案中,一般用1 表示黑像素,以0 表示白像素,这与现在计算机的色彩表示正好相反,不利于计算机处理.为此,文献[7-8]提出了与计算机色彩表示方式相同的方案.若无小型计算设备,则该方案可以通过叠加解密恢复秘密图像;若有小型计算设备,则该方案通过异或解密恢复秘密图像,因此恢复秘密图像的视觉质量更好.
传统视觉密码方案产生的分享份均为噪声无意义图像,不利于区分并管理分享份.文献[9]提出了一种基于随机网格的标记视觉密码方案,只是恢复的秘密图像比较模糊,且恢复图像的视觉质量无法调节,不具有灵活性.文献[10]则拓展了现有的概率型视觉密码方案,有助于灵活调节恢复图像的视觉质量,但也存在像素扩展和设计加密矩阵的问题.
针对以上问题,本文提出一种基于异或解密的标记视觉密码方案.该方案采用与计算机相同的颜色表示方式以便计算机处理;通过随机网格不但能够避免像素扩展和设计加密矩阵的问题,而且可以灵活调节标记信息的嵌入比例;在解密过程中使用异或解密,提高了恢复的秘密图像和标记图像的视觉质量.
1 视觉密码现有方案介绍
1.1 (k,n)随机网格视觉密码方案
文献[11-15]研究并改进了随机网格视觉密码,下面简要介绍文献[15]是如何通过改变随机像素产生的方式提高恢复秘密图像视觉质量的,其加密流程如下:
输入大小为M ×N 的二值秘密图像S;
输出n 幅分享份R1,R2,···,Rn;
步骤1对于秘密图像中的像素s(i,j),1iM,1jN,重复执行步骤2 ∼5;
步骤2随机产生k −1 个布尔向量bv,1vk −1;
步骤3令第k 个像素bk=s(i,j)⊕b1⊕...⊕bk−1,其中⊕表示异或运算;
步骤4令bk+1=bk,bk+2=bk,··· ,bn=bk;
步骤5将生成的n 个像素b1,b2,··· ,bn随机分配到n 幅随机网格R1,R2,··· ,Rn的相同位置上,即R1(i,j),R2(i,j),··· ,Rn(i,j);
步骤6生成n 幅分享份R1,R2,··· ,Rn.
该方案改进了基于随机网格的视觉密码方案,但因为生成的分享份是无意义的噪声图像,所以容易与其他分享份混淆,不利于识别和管理.
1.2 视觉密码相关定义
定义1对于M ×N 的二值秘密图像S,其平均光通量D(S)为

式中,白像素光通量为1,黑像素光通量为0,由此可知秘密图像S 的平均光通量等价于白像素在秘密图像中出现的概率.
定义2解密后恢复图像的对比度可表示为
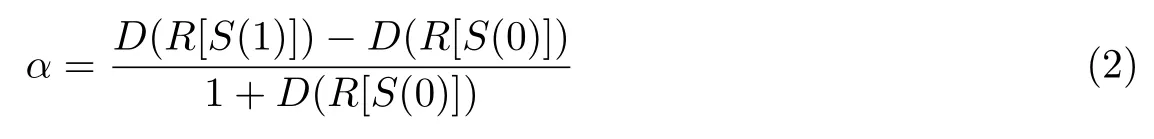
式中,S(1) 表示二值秘密图像S 中白像素的区域,S(0) 表示黑像素的区域,S = S(0)∪S(1),S(0)∩S(1)=∅.R[S(0)]、R[S(1)]分别表示解密后的恢复图像R 中与S(0)、S(1)处于相同位置的区域.
定义3当对比度α = 0、D(RS[S(1)]) = D(RS[S(0)])时,解密后白像素概率等于黑像素概率,此时不能恢复秘密图像信息;当对比度α>0、D(RS[S(1)])>D(RS[S(0)])时,解密后图像就能恢复秘密图像信息.
定理1由定义2 可得,有效的标记视觉密码方案需符合以下3 种条件:
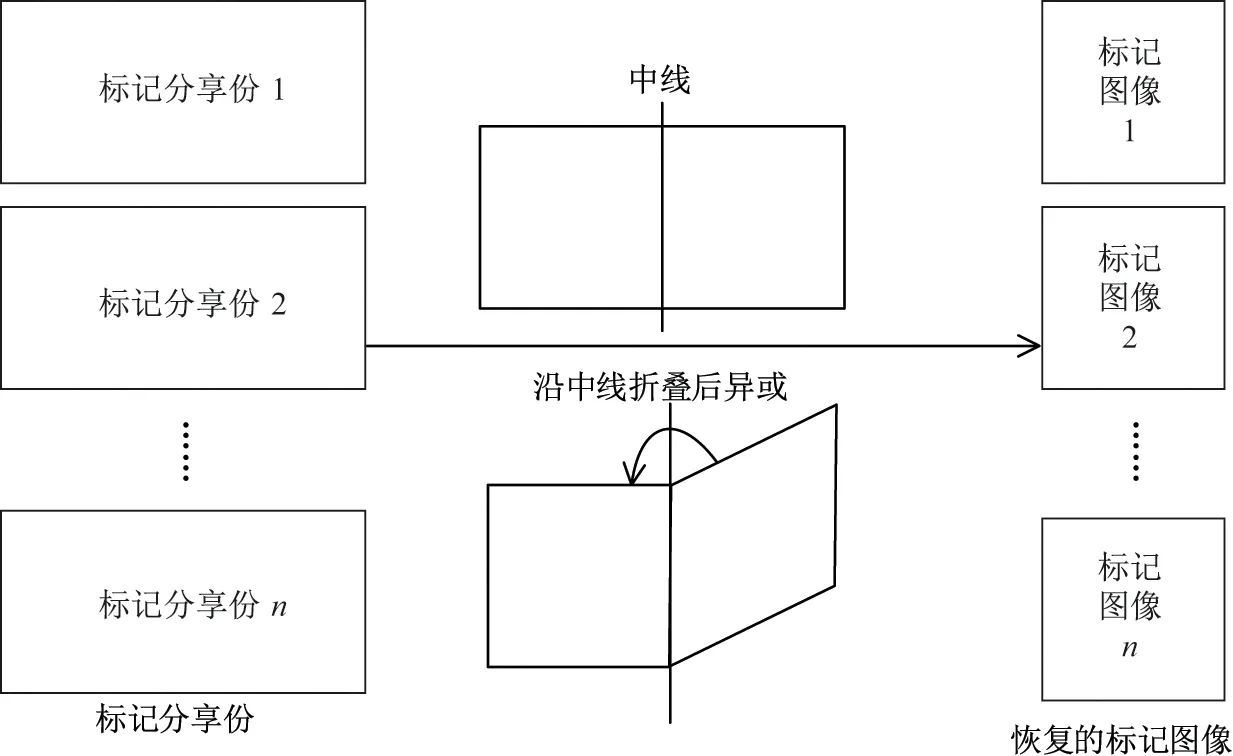
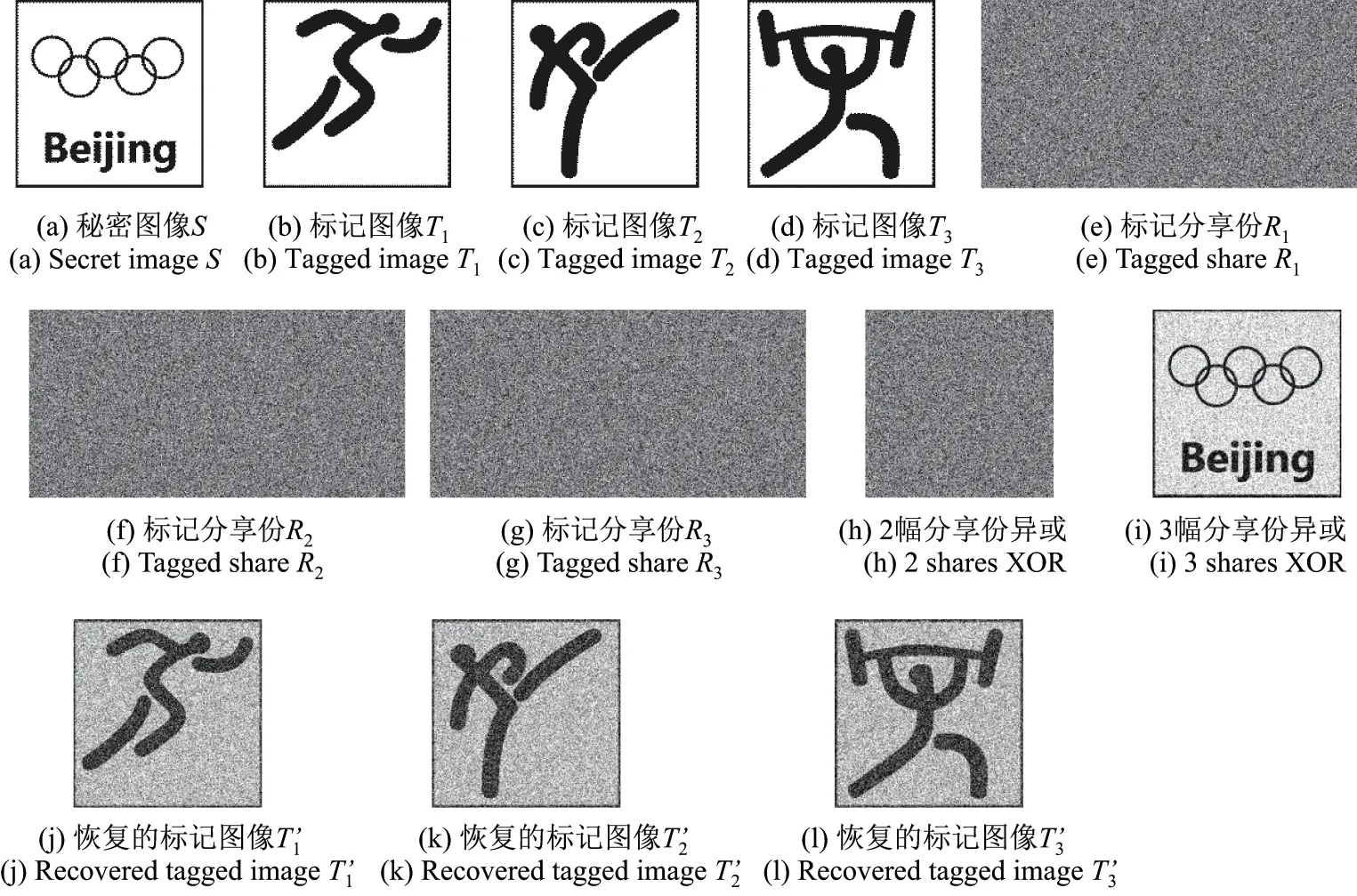
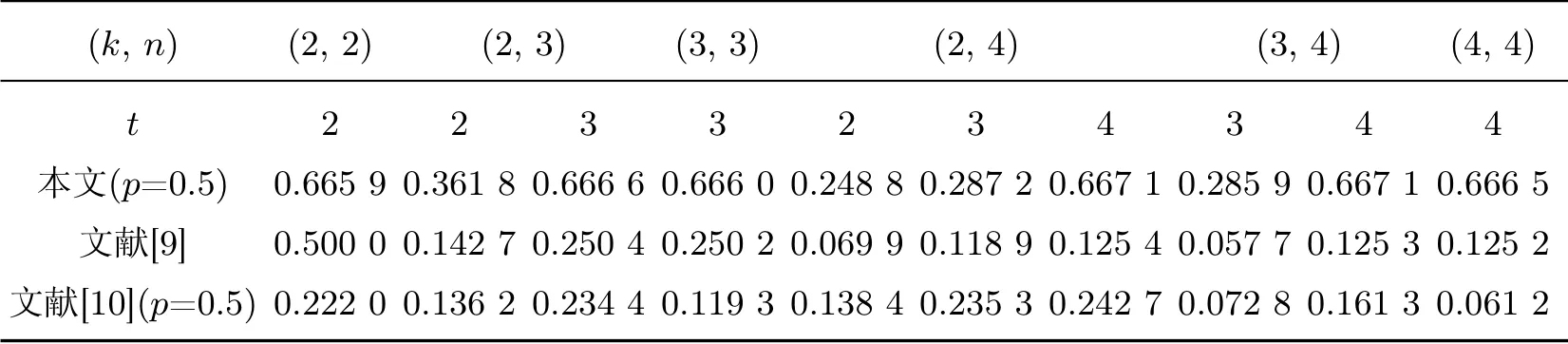
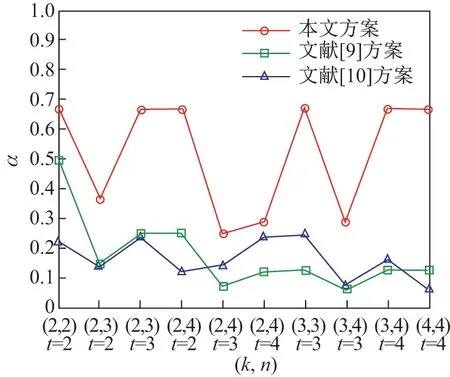
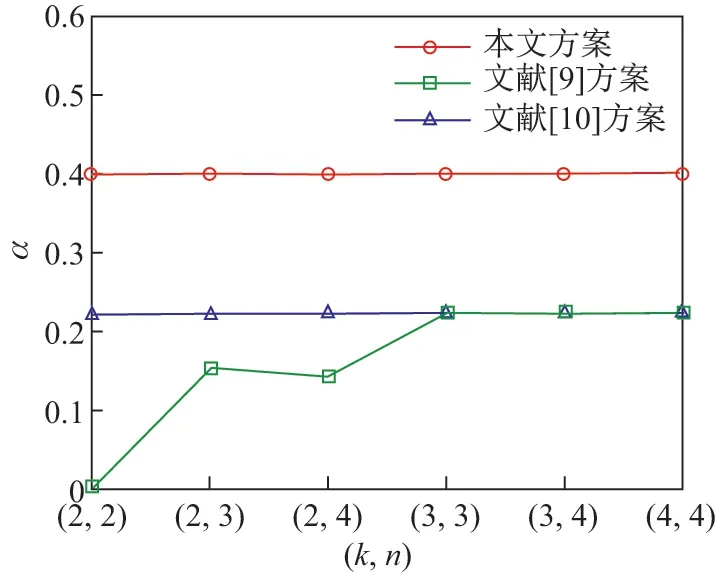
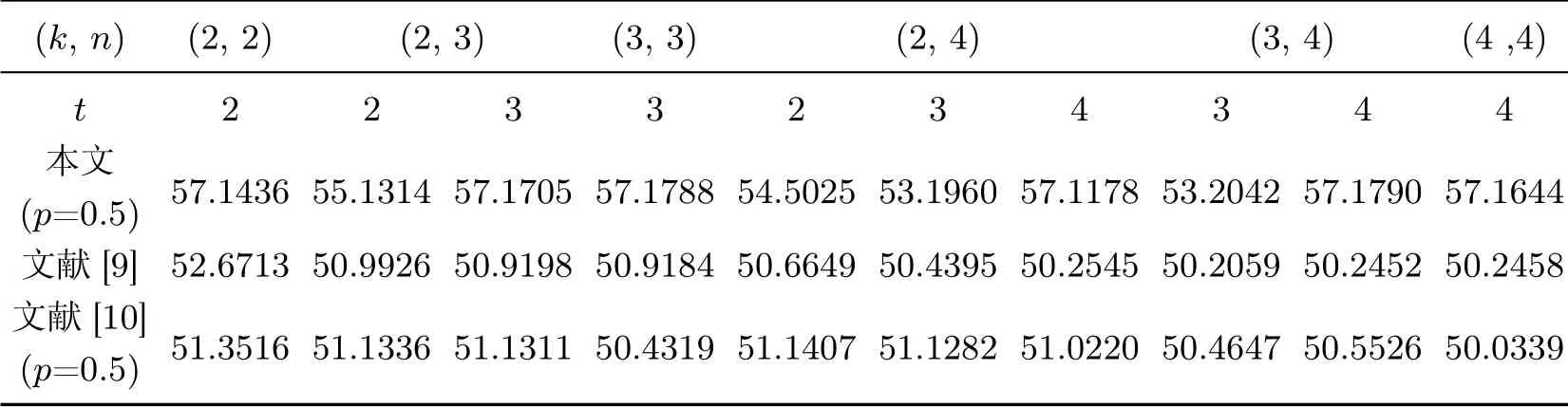
条件1当t 条件2当tk 时,任意t 幅标记分享份异或后可以恢复秘密图像信息 条件3将任意标记分享份Rx折叠后进行异或解密可恢复相应的标记信息 式中,S 为秘密图像,T1,T2,··· ,Tn为n 幅标记图像,R1,R2,··· ,Rn为加密后生成的标记分享份.RS表示任意t 幅标记分享份Rx1,Rx2,··· ,Rxt异或解密后恢复的秘密图像,{x1,x2,··· ,xt} ⊂{1,2,··· ,n};RT表示任意一幅标记分享份Rx异或解密后恢复的标记图像,x=1,2,··· ,n.T(1)和T(0)分别表示标记图像中白像素和黑像素所在区域. 本文设计了一种基于异或解密的标记视觉密码方案,并改进了文献[9-10]的方案.该方案在普通分享份中嵌入标记信息,通过采用异或解密方式提高了恢复图像的视觉质量. 输入M ×N 的二值秘密图像S 以及n 幅M ×N 的二值标记图像T1,T2,··· ,Tn,并标记图像嵌入概率p. 输出n 幅M ×2N 的标记分享份R1,R2,··· ,Rn. 步骤1对于任意给定的秘密像素s(i,j),执行步骤2∼12. 步骤2随机生成k −1 个布尔数bv,1vk −1. 步骤3若k 为奇数,则第k 个像素bk= s(i,j)⊕b1⊕···⊕bk−1;若k 为偶数,则第k个像素 步骤4令bk+1=bk,bk+2=bk,··· ,bn=bk. 步骤5将生成的b1,b2,··· ,bn随机分配到随机网格R1(i,j),R2(i,j),··· ,Rn(i,j)中. 步骤6随机生成k 个布尔数, u=1,2,··· ,k. 步骤7若k 为偶数,则第k+1 个像素若k 为奇数,则第k+1 个像素 步骤8令 步骤9将生成的随机分配到随机网格R1,R2,··· ,Rn的相同位置上,即随机网格R1(i,N +j),R2(i,N +j),··· ,Rn(i,N +j). 步骤10随机生成布尔数a,且a 取0 的概率为p.当a = 0时,重复执行步骤11;当a=1 时,返回步骤1,直至生成所有标记分享份. 步骤11随机生成布尔数b,且b 取0 或1 的概率相等;根据式(6)更改每一分享份Rx的像素Rx(i,j) 步骤12输出n 幅标记分享份R1,R2,··· ,Rn. 在加密过程中,已标记分享份的左半部分首先以文献[10]的(k,n)方案进行加密,而右半部分则用文献[10]的(k+1,n)方案进行加密;然后标记图像Tx的信息并根据概率选择是否嵌入分享份Rx而生成最终标记分享份,其中概率p 的大小决定了标记信息嵌入标记分享份的比例.概率p 的值越大,嵌入的标记信息比例越高,解密恢复的标记图像越清晰. 解密秘密图像时,交替使用标记分享份的左右两部分进行解密,此时恢复的秘密图像无像素扩展.对于给定的标记分享份Rx(i,j)t = 1,2,··· ,t,其中t 为恢复秘密图像所用的标记图像分享份数量,当t −k 为偶数时,使用式(7)解密;当t −k 为奇数时,使用式(8)解密. 采用本文方案解密标记图像时,先将标记分享份沿中线折叠,再对折叠后相同位置上的像素进行异或运算,即根据式(8)解密n 幅标记分享份R1,R2,··· ,Rn.解密后的标记图像大小与原图像大小相同,且无像素扩展现象.解密过程如图1 所示. 图1 本文方案标记图像的解密Figure 1 Decryption of tagged image in this paper 引理1对于随机生成的t 个像素b1,b2,··· ,bt,借鉴通常的集合表示方法,令r =则r 的平均光通量为D(r)=1/2. 证明 1)当t=2 时,r =b1⊕b2.若b1=0,b2=0 或b1=1,b2=1,则r =0;若b1=0,b2=1或b1=1,b2=0,则r =1.即r 为0 和1 的概率相等,此时光通量D2(r)=1/2. 2)设t−1 个随机生成的像素异或后的光通量Dt−1(r)=1/2,对于t 个像素b1,b2,··· ,bt,若则t 个像素异或结果为0;若或则这t 个像素异或结果为1,t 个像素异或后结果为黑、白像素的概率相等,即Dt(r)=1/2. 由数学归纳法可得,随机生成的t 个像素异或后的平均光通量为D(r)=1/2. 引理2秘密图像加密后生成的每幅标记分享份均为噪声无意义图像. 证明令s 表示秘密像素,由本文加密过程可知:当k 为奇数时,前k −1 个像素随机生成,第k 个像素bk=s(i,j)⊕b1⊕···⊕bk−1.若s=0,则若s=1,则···⊕bk−1.因为b1是随机产生的,显然b1也是随机产生的,所以由k −1 个随机数得到的bk是随机产生的.当k 为偶数时,同样可以得到生成的标记分享份中每个像素均为随机生成,且黑像素、白像素的概率相同,则每幅标记分享份的平均光通量D(Rx[S(1)])=D(Rx[S(0)]). 由式(2)可得每幅标记分享份的对比度α=0,即证明了秘密图像加密后生成的每幅标记分享份均为噪声无意义图像. 引理3任意t(t 证明标记分享份中既包含秘密信息,又包含标记信息,于是分别以bx1,bx2,··· ,bxt和表示标记分享份中处于相同位置的包含秘密信息的像素和包含标记信息的像素,{x1,x2,··· ,xt} ⊂{1,2,··· ,k},再令r 表示bx1,bx2,··· ,bxt异或解密的结果,r'表示异或解密的结果. 对于包含秘密信息的t 个像素bx1,bx2,··· ,bxt来说,可分为k{x1,x2,··· ,xt} 和k ∈{x1,x2,··· ,xt}两种情况进行讨论. 2) 当k ∈{x1,x2,··· ,xt} 时,假设有q 个像素从b1,b2,··· ,bk−1中选择,t −q 个像素从bk,bk+1,··· ,bn中选择,则从b1,b2,··· ,bk−1中选择的q 个像素是随机产生的,从bk,bk+1,··· ,bn中选择的t −q 个像素是相同的.同时,因q < t < k,这t 个像素之间和秘密像素s 相互独立,则t 个像素异或后光通量D(r[s=0])=D(r[s=1])=1/2. 综上所述,D(RS[S(1)]) = D(RS[S(0)]),即证明了当t < k 时,t 幅标记分享份异或不能恢复出任何信息. 引理4任意t(tk)幅标记分享份异或可以恢复秘密图像信息. 证明对于包含秘密信息的像素bx1,bx2,··· ,bxt来说,当t −k 为偶数时,在这t 个像素中,假设从b1,b2,··· ,bk−1中选择q 个像素,在bk,bk+1,··· ,bn中选择t −q 个像素. 情况1q =k−1.出现该情况的概率为此时t−k 为偶数且q =k−1,t−q为奇数,即在bk,bk+1,··· ,bn中有奇数个像素被选中.由加密流程可知bk=bk+1=···=bn,所以这t −q 个像素异或之后的光通量与单个像素bk的光通量相同,即这t 个像素异或就相当于b1,b2,··· ,bk异或.又因为bk= s(i,j)⊕b1⊕···⊕bk−1,所以这t 个像素异或后的光通量可表示为D(r[s=1])=1 且D(r[s=0])=0. 情况2q=0.出现该情况的概率为此时这t 个像素都是从bk,bk+1,··· ,bn中选择的,它们相同且都是随机生成的.无论秘密像素s 是黑像素还是白像素,若t 为偶数,则解密后光通量为D(r[s = 0]) = D(r[s = 1]) = 1;若t 为奇数,则D(r[s = 0]) = D(r[s =1])=0. 情况30 < q < k −1.出现该情况的概率为而且这种情况与引理3 中k ∈{x1,x2,··· ,xt}的情况相似,此时t 个秘密信息像素异或解密后的光通量表达式为D(r[s=0])=D(r[s=1])=1/2. 情况1q =k −1.出现这种情况的概率为中的情况1 类似,此时秘密信息像素异或解密后的光通量为D(r[s=1])=1,D(r[s=0])=0. 情况20< q < k −1.这种出现情况的概率为与②中的情况3 类似,此时秘密信息像素异或解密后的光通量为D(r[s=0])=D(r[s=1])=1/2. 因此,当t −k 为偶数时,秘密信息的像素bx1,bx2,··· ,bxt异或解密后的光通量的表示式为 同理可证,当t −k 为奇数时,秘密信息的像素bx1,bx2,··· ,bxt异或解密后的光通量为 综上所述,D(RS[S(1)])>D(RS[S(0)]),即证. 引理5折叠任意一幅标记分享份后进行异或解密可以恢复相应标记信息. 证明令tx1,tx2和分别表示在任意一幅标记分享份Rx中关于中线对称位置上包含秘密信息的像素和包含标记信息的像素,当沿中线折叠任意一幅标记分享份Rx并进行异或运算时,由于包含秘密信息的像素tx1和tx2之间互不相关,D(rT[Tx(0)]) = D(rT[Tx(1)]) = 1/2.对于包含标记信息的像素和则D(RT[Tx(1)])>D(RT[Tx(0)]),即沿中线折叠任意一幅标记分享份后进行异或解密可以恢复相应标记信息. 通过视觉密码加密后恢复的图像会丢失部分信息,可能出现恢复的图像视觉质量下降甚至无法识别其中信息的情况;而对于文本图像或简单图案,虽然解密后恢复的视觉质量有所下降,但仍可识别解密图像中所含信息.为验证本文方案的有效性,分别以文本图像和简单图案作为秘密图像进行(3, 3)情况下的仿真实验,所得结果如图2 和3 所示. 图2 p=0.5 时文本图像在(3, 3)情况下的仿真结果Figure 2 Simulation results for text image (3, 3) when p=0.5 图3 p=0.5 时简单图案在(3, 3)情况下的仿真结果Figure 3 Simulation results for simple image (3, 3) when p=0.5 由仿真结果可知:对于文本图像和简单图案,经过视觉密码加密后恢复的图像损失了部分秘密信息,但仍能识别解密后图像中所含信息.秘密图像加密后产生的标记分享份类似于噪声图像,这样就不会泄露秘密图像信息;经过异或解密恢复的秘密图像和标记图像大小与原图像相同,无像素扩展.若少于k 幅标记分享份图像参与异或解密,则无法恢复秘密图像的信息;若k 幅或多于k 幅标记分享份图像参与异或解密,则能恢复相应的秘密图像信息.通过改变嵌入标记信息的概率p,可以有效调节恢复的标记图像的视觉质量. 在视觉密码中,对比度是非常重要的参数.对比度越大,恢复图像越清晰,反之则越模糊.在不同情况下,使用本文方案对文本图像和简单图案进行加密恢复的图像对比度分别由表1和2 给出,其中嵌入标记信息的概率p 取0.5,t 表示参与解密的分享份数目.因为标记分享份的产生具有随机性,所以每次实验得到的对比度会发生变化,于是本文取10 次实验结果的平均数作为对比度值. 表1 不同情况下恢复的秘密图像的对比度Table 1 Contrast of recovered secret image in different circumstances 表2 不同情况下恢复的标记图像的对比度Table 2 Contrast of recovered tagged image in different circumstances 由表1 和2 可知:在误差允许范围内,文本图像和简单图案在相同情况下恢复的秘密图像和标记图像的对比度可视为相同. 采用简单图案进行加密并分别比较本文方案、文献[9]方案、文献[10]方案在(2, 3)情况下恢复的秘密图像和标记图像,其中标记信息嵌入概率p=0.5. 为进一步分析本文方案、文献[9]方案、文献[10]方案恢复的秘密图像的对比度,通过计算得出3 种方案在不同情况下恢复的秘密图像对比度,如表3 所示,图4 为表3 折线图.由表3 和图4 可以得出:在(2, 2)和(2, 3)情况下,文献[9]方案的对比度略高于文献[10]方案的对比度,但在(3, 3)和(3, 4)情况下文献[10]方案的对比度高于文献[9]方案的对比度,而本文方案恢复的秘密图像的对比度在所有情况下都是这3 种方案中最高的,且当所有标记分享份都参与解密时,恢复的秘密图像对比度可达0.66. 表3 本文方案、文献[9]方案、文献[10]方案恢复的秘密图像对比度比较Table 3 Comparison of secret image contrast among the proposed scheme and related methods in Reference [9]and [10] 图4 不同方案恢复的秘密图像对比度Figure 4 Contrast of secret images for different schemes 通过计算得出3 种方案在不同情况下恢复的标记图像对比度,如表4 所示,图5 为表4 的折线图.由表4 和图5 可看出:文献[9]方案恢复的标记图像的对比度普遍偏低,在(2, 2)、(2,3)、(2, 4)、(3, 3)情况下恢复的标记图像对比度呈上升趋势,在(3, 4)、(4, 4)情况下则趋于平缓;文献[10]方案恢复的标记图像的对比度则约为0.22,在(2, 2)、(2, 3)、(2, 4)情况下相较于文献[9]方案恢复的标记图像的对比度有所提高;本文方案恢复的标记图像的对比度约为0.4,与文献[9]方案和文献[10]方案相比,本文方案经过异或解密后的标记图像具有更高的对比度. 表4 本文方案与文献[9]方案、文献[10]方案恢复的标记图像对比度比较Table 4 Comparison of tagged image contrast between the proposed scheme and related methods in Reference [9]and [10] 峰值信噪比(peak signal to noise ratio, PSNR)是一种使用最广泛的图像客观评价指标,PSNR 数值越大表示失真越小.通过计算得出在不同情况下3 种方案恢复的秘密图像和标记图像的PSNR,如表5 和6 所示. 图5 不同方案恢复的标记图像对比度Figure 5 Contrast of tagged images for different schemes 表5 本文方案与文献[9]方案、文献[10]方案恢复的秘密图像PSNR 比较Table 5 PSNR of the secret image contrast between the proposed scheme and related methods in Reference [9]and [10]dB 表6 本文方案与文献[9]方案、文献[10]方案恢复的标记图像PSNR 比较Table 6 PSNR of the tagged image contrast between the proposed scheme and related methods in Reference [9]and [10]dB 由表5 和6 可知:就恢复的秘密图像的PSNR 而言,本文方案均高于文献[9]方案和文献[10]方案,失真更小,且当全部分享份参与解密时的PSNR 大于等于57 dB.对于恢复的标记图像,本文方案的PSNR 也高于文献[9]方案和文献[10]方案的PSNR,失真小. 综上所述,与文献[9]方案相比,本文方案使用随机网格构造视觉密码方案,恢复的秘密图像无像素扩展现象,于是可以根据需要调节标记图像嵌入概率,从而改变恢复的秘密图像的视觉质量,同时通过异或解密提高恢复的秘密图像和标记图像的视觉质量.与文献[10]方案相比,本文方案不存在像素扩展和设计加密矩阵问题,故恢复秘密图像的视觉质量更好. 本文提出了一种基于异或解密的标记视觉密码方案,在加密过程中使用随机网格方法,无需设计加密矩阵;采用与计算机数字图像相同的色彩表示方式是便于计算,这在当今互联网高速发展的时代具有更加广泛的意义.在解密过程中采用异或解密方法,有效提高了恢复的秘密图像和标记图像的视觉质量,且恢复的秘密图像和标记图像无像素扩展现象.此外,通过在分享份中嵌入可调节比例的标记信息而使本文方案灵活多变,用户体验更加友好. 视觉密码技术算法简单,得到了人们的广泛认可.本文方案可以在生成的标记分享份中隐藏标记图像信息,不仅有助于分享份的识别与管理,还能防止分享图像信息被恶意篡改的欺骗行为.同时,在标记分享份中隐藏附加信息的能力进一步丰富了应用场景,如数字签名、核实身份的身份认证、数字水印等场景.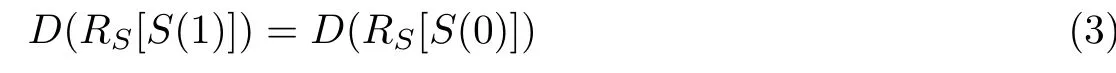


2 基于异或解密的视觉密码方案
2.1 加密过程
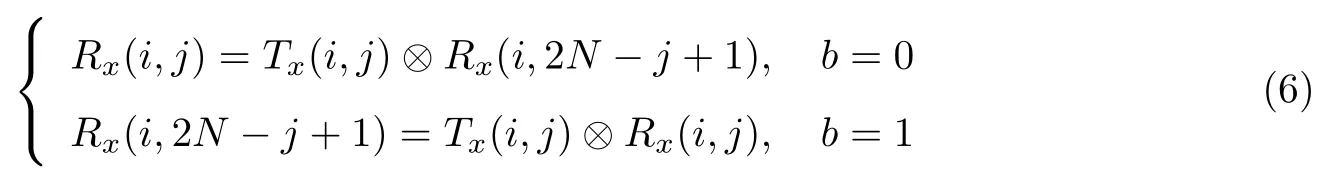
2.2 解密过程
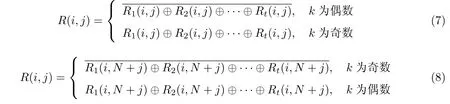
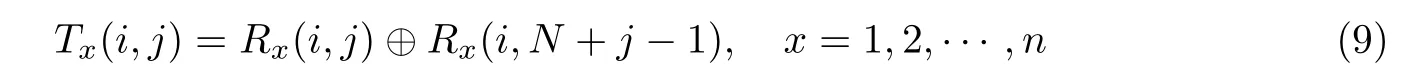
3 性能分析
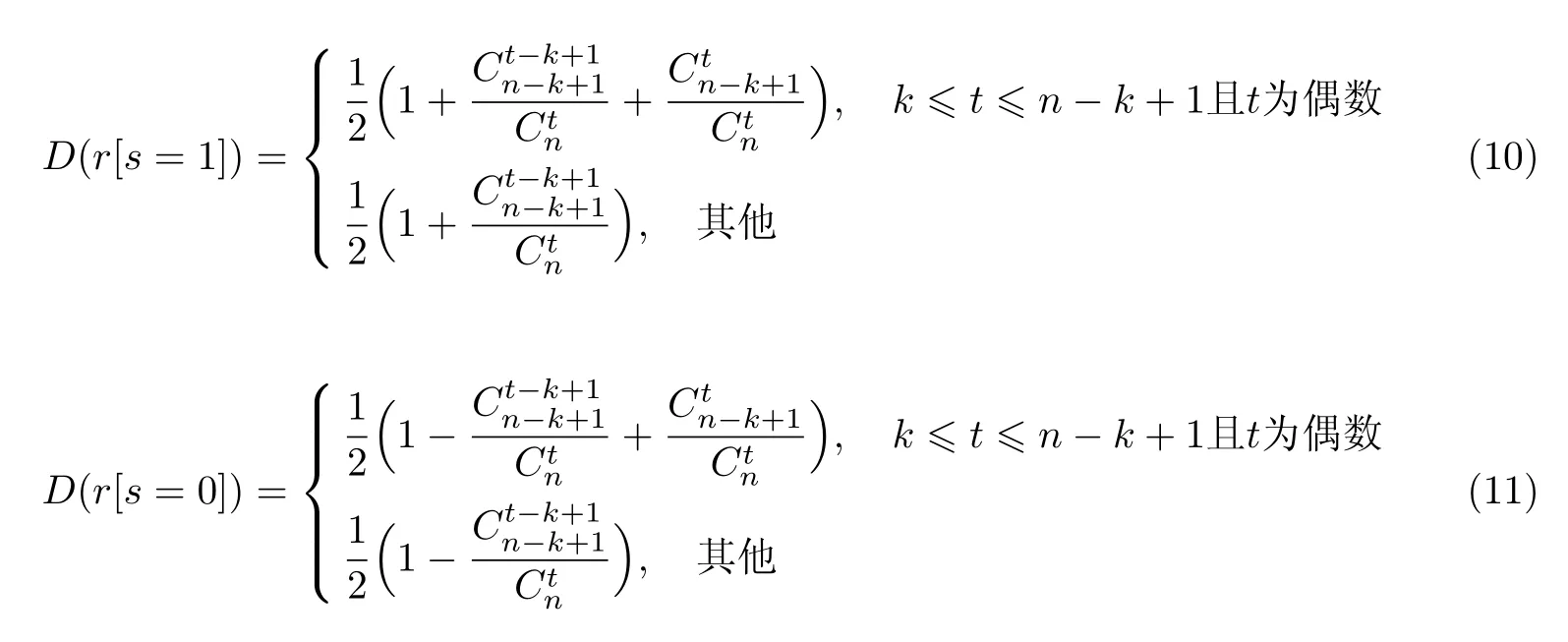

4 实验及结果分析
4.1 本文方案的仿真结果

4.2 解密图像对比度


5 相关方案比较
5.1 恢复图像对比度比较

5.2 恢复图像峰值信噪比比较

6 结 语

