浅谈“判断函数奇偶性”的几种情形

靳亦朴

(河北省邯郸市第三中学 056001)

掌握判断函数的奇偶性的方法和步骤，是本章节的重点和难点.在老师的指导下，我试图通过实例归纳了这类问题的求解方法.

函数的奇偶性是函数的“整体”性质.一般地，如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就称作偶函数；如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),则函数f(x)为奇函数.判断函数的奇偶性，应严格按照函数奇偶性的判断步骤进行.

首先，根据解析式求出其定义域，若其定义域不关于原点对称，则函数为非奇非偶函数.

一、判断下列函数的奇偶性

(1)f(x)=0,x∈(-1,1]；

分析首先确定函数的定义域，可以事半功倍.

解(1)函数的定义域为(-1,1]，不关于原点对称，所以该函数既不是奇函数，也不是偶函数.

(2)函数的定义域{2}，不关于原点对称，所以该函数既不是奇函数，也不是偶函数.

其次，若其定义域关于原点对称，再判断f(-x)与f(x)的关系.若f(-x)=f(x)则函数为偶函数；若f(-x)=-f(x)，则函数为奇函数.

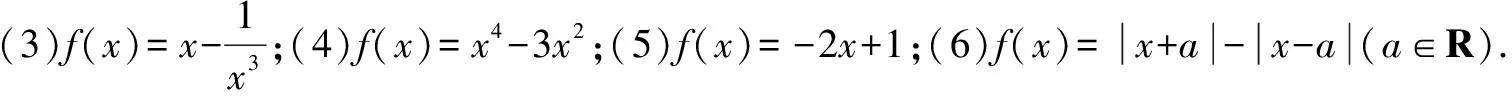
解(3)函数的定义域是(-∞，0)∪(0，+∞)，关于原点对称.当x∈(-∞,0)∪(0,+∞)时，显然-x∈(-∞,0)∪(0,+∞).

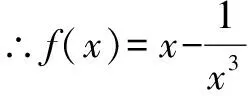
(4)函数的定义域是R,关于原点对称.

∵f(-x)=(-x)4-3(-x)2=x4-3x2=f(x),

∴该函数为偶函数.

(5)函数的定义域为R,关于原点对称.∵f(-x)=-2(-x)+1=2x+1≠f(x),-f(x)=-(-2x+1)=2x-1,f(-x)≠-f(x),

∴该函数既不是奇函数，也不是偶函数.

(6)∵函数f(x)的定义域为R，关于原点对称.

当a≠0时，f(-x)=|-x+a|-|x-a|=|x-a|-|x+a|=|x+a|-|x-a=-f(x),

此时，函数为奇函数.

当a=0时，f(x)=|x+a|-|x-a|=|x|-|x|=0，

∴f(-x))=f(x))=0,且f(-x))=f(x)=0,

此时，函数f(x)既是奇函数，又是偶函数.

综上可知，当a∈R，且a≠0时，函数f(x)为奇函数；当a=0时，函数f(x)既是奇函数，又是偶函数.

二、判断分段函数的奇偶性

首先要判断函数的定义域是否关于原点对称；其次，如果其定义域关于原点对称，要分段讨论，必须判断每一段是否都具有f(-x)=f(x)或f(-x)=-f(x)的特征.

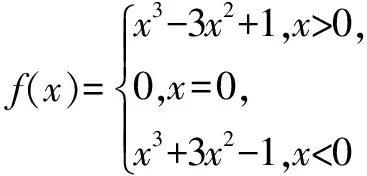
分析首先要特别注意x与-x的范围，然后将它们代入相应区间的函数表达式中，f(x)与f(-x)一般对应不同的表达式，再按照奇偶函数的定义进行判断或证明.

解f(x)定义域为R，关于原点对称.

当x>0时，-x<0,∴f(-x)=-x3+3x2-1=-(x3-3x2+1)=-f(x);当x=0时，-x=0,∴f(-x)=f(0)=0,f(x)=f(0)=0,f(-x)=-f(x);当x<0时，-x>0,则f(-x)=-x3-3x2+1=-(x3+3x2-1)=-f(x).

综上，当x∈R时，总有f(-x)=-f(x),∴f(x)为奇函数.

三、抽象函数的奇偶性

在判断此类函数的奇偶性时，需要判断f(-x)与f(x)的关系；也可以根据f(x)±f(-x)是否为0来判断两者的关系.

例4如(8)函数f(x),x∈R，若对于任意实数a,b,都有f(a+b)+f(a-b)=2f(a)f(b)，求证：f(x)为偶函数.

分析f(x)的定义域为R,定义域关于原点对称,欲证明f(x)为偶函数,只需要证明f(-x)=f(x)即可.

证明由题意知f(x)的定义域为R，∴定义域关于原点对称.

∵对于任意的a,b∈R都有f(a+b)+f(a-b)=2f(a)f(b),

∴b=0,2f(a)=2f(a)f(0).若f(a)=0,a是任意实数，则f(x)=0,显然是偶函数.

若f(a)≠0，则f(0)=1.再令a=0,f(b)+f(-b)=2f(0)f(b)=2f(b),f(-b)=f(b).

∴该函数是偶函数.

此外，判断函数的奇偶性还可以根据函数图象的对称情况进行判断.若函数的图象关于原点(y轴)对称，则函数为奇函数(偶函数)，否则就不具有奇偶性.

在学习这章节时，通过练习典型的例题，通过细微而敏锐的观察，进而联想转化.对于每一道题，无论难易，冷静对待，牢记解题方法和技巧，养成良好习惯，提高数学素养.