三角函数中数与形手牵手
吴 娟
(江苏省昆山中学 215300)
普通高中数学学科核心素养之一是直观想象,直观想象是指借助几何直观感知实物的形态与变化,利用图形理解和解决数学问题的过程.华罗庚先生曾指出“数缺形时少直观,形少数时难入微;数形结合百般好,隔裂分家万事非.”数形结合思想是高中数学重要的思想方法.本文主要就数形结合思想在三角函数学习中的应用与大家一起探讨.
一、数形结合概念
1.数形结合思想
数学中,数与形是两个最主要的研究对象.“数形结合”思想是把数或数量关系与图形对应起来,借助图形来研究数量关系或者利用数量关系研究图形的性质.它们在内容上相互联系,方法上相互渗透,在一定条件下可以相互转化.恩格斯是这样定义数学的:“数学是研究现实世界的量的关系与空间形式的科学.”这就意味着数形结合是数学的本质特征,宇宙间的万事万物是数与形和谐的统一,因此数形结合思想是数学的精髓与灵魂.
数形结合是研究数学问题并解决问题的模型转化的一种基本思想与基本方法.它能沟通数与形的内在联系.具体来说就是在研究问题的过程中既分析其代数含义,又揭示其几何意义,使数量关系和几何形式巧妙、和谐的结合起来,充分利用这种结合,寻找解决问题的思路,使抽象问题直观化,复杂问题简单化,从而使问题得以解决的一种重要的数学思想.
2.数形结合的价值
数形结合思想是中学数学重要的思想方法之一,在高中的数学学习中发挥着重要的作用.
首先,学生巧妙应用数形结合思想能掌握到更多的知识点,也能使学生对整体的知识点进行把控,形成良好的知识脉络,将各类知识点融会贯通;并且也能有效改善学生的思维能力和解题思路,为他们提供更多的学习方法和解题思路,也能为学生提供更多的学习认知规律.
其次,正确的运用数学结合思想,能有效地培养学生的数学思维能力,丰富学生的思维方式.有利于对学生思维、兴趣的培养,从而不仅可以减轻学生的负担,也能给学生创造更好的学习思维方式.
再次,学会怎样运用数形结合思想,也能帮助学生在学习中树立良好的学习思想和学习习惯.可以帮助学生从多角度多层次思考问题,形成良好的思维方式;教导学生学会将抽象的问题具体化,更准确地把握问题本身;可以锻炼学生的思维模式,也能锻炼他们的创造能力的思维发展.
二、数形结合思想在三角函数中的应用
“依性作图,以图识性”是数形结合思想的重要体现.三角函数在本质上是对单位圆圆周上一点运动的“动态描述”,它的种种性质和公式都是和单位圆的几何性质密切关联的,这就要求在解决三角函数的相关问题上,应巧妙地运用单位圆中的三角函数线和三角函数图形,以形助数,数形结合.数形结合贯穿了三角函数的整个章节,三角函数在单位圆中的定义得出了三角函数线、三角函数的图象、图象的变化等都需要图象的支持.
1.利用数形结合,有利于学习难点化解
在推导三角函数的诱导公式时,教科书上是从代数(三角函数的坐标定义)的角度推导的,我们也可以利用三角函数的几何表示(三角函数线)来推导.单位圆中的三角函数线可以使抽象问题直观化、生动化,变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性和灵活性的有机结合,也为学生的学习提供更广阔的思维空间.
片段一:终边相同的角的同一三角函数值相等.
如图1,P是半径为1的圆O上一点,点P的运动可以形象的描述为“周而复始”.当点P旋转一周时又回到了原来的地点,由三角函数线可知终边相同的角的同一三角函数值相等.
片段二:如果角α的终边与角β的终边关于x轴对称.
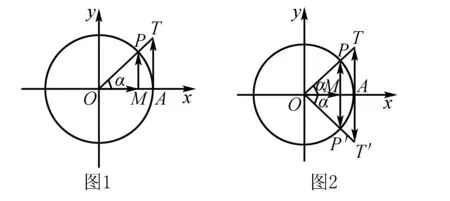
如图2,设角α、β的终边分别与单位圆交于P、P′,分别与x=1交于T,T′,由三角函数线可知sinα=MP,cosα=OM,tanα=AT;sinβ=MP′,cosβ=OM,tanβ=AT′;即:sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα.
当角α的终边与角β的终边关于y轴、原点对称,学生类比以上方法很快得出一系列的诱导公式.
在图示中,先取α为锐角,关于x轴对称,作出-α;关于y轴对称,作出π-α;关于原点对称,作出π+α,利用三角函数线很容易得出书上的诱导公式.但当α不是锐角时,这些结论依然成立吗?我们可以用坐标即三角的代数定义来严格证明.
在这学习的过程中利用三角函数线的推导体现了图形的直观性,学生很容易接受;再用坐标的代数证明又体现了数学的严谨性.学生掌握了诱导公式的本质,了解公式的来龙去脉,在理解中记忆,方能掌握得更扎实、更透彻,也为学生的学习提供更广阔的思维空间.
2.利用数形结合,拓展解题思路
学生甲:作差
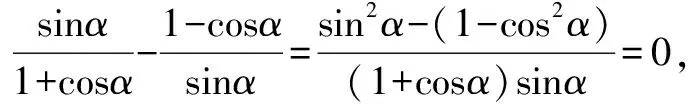
学生乙:观察对角关系
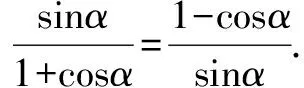
教师:还有其他想法吗?这个式子能用图形来解释吗?

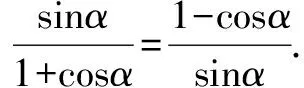
本题的数形结合揭示了三角函数在单位圆中的定义的本质特征,在具体的教学过程中,引导学生主动地探索、发现、领会其中的联系.数学知识与图形有着密切的联系,以具体的数学知识为载体、潜移默化地将数形结合的思想不断渗透,随着数形结合的思想不断体现,学生认知也会不断发展和逐渐深化,同时不断提升学生的创新意识和创新能力.
片段四 若α为锐角(单位为弧度),试利用单位圆及三角函数线,比较α,sinα,tanα之间的大小关系.
生甲:画单位圆,利用三角函数线,可以得到sinα 教师:本题的难点在于α的转化,我们怎么把α转化出来 呢? 教师:弧AP是曲线,怎么比较大小呢?我们该如何利用图形证明? 生丙:因为S△AOP 学生们都鼓起了掌,觉得非常的巧妙. 教师:非常好,本题的难点就在于要把α转化,先把α转化成弧长,再利用三角形和扇形的面积大小得出结论,所以图形在三角中也起着非常重要的作用,数与形的结合使抽象的问题具体化,形象化,学生很乐意的接受了. 在教学过程中我们既要关注数学知识,更要揭示和显化蕴含在其中的数学思想方法,这样数学知识不再是孤立的、零散的,而是具有了一定的联系性、整体性与灵活性;我们不仅传授数学知识,更要展示数学思维的美妙,引导学生体验数学探索的过程.数学知识是数学思想方法的重要载体,数形结合思想方法在以上习题中的应用开阔了学生分析问题的视野,拓展了学生的思维、提升了学生转化问题解决问题的能力. “数”与“形”的转化与结合不仅是一种重要的解题方法与策略,更是一种重要的数学思维与思想方法.首先需要的是一种意识:敏锐捕捉信息,恰当的时候建立适当的联系;其次是一种转化思想:根据数的结构特征,构造出与之相应的图形,并利用图形的性质和规律解决“数”的问题;再次是一种能力、一种思考的方式.在教学的过程中,让学生了解数形结合思想产生的背景,把握数形结合思想的本质,感受数形结合思想的价值,形成良好的数学意识与数学思想.数与形相辅相成,和谐统一,完美结合,让我们一同感受与体会数学之美,“数”与“形”牵手之妙.

