匀速圆周运动的三个难点剖析

刘桂斌

(广东省佛山市南海区第一中学 528200)

匀速圆周运动是高一物理教学的重要运动模型，不仅是教学和考试考查的重点，并且和社会、生活、科技联系紧密，具有很强的实用性和应用性.在教学过程中，由于高一学生物理知识、数学工具的运用能力和思维能力等相对不足，学生对匀速圆周运动的几个问题比较难掌握，一是向心加速度的大小和方向的推导；二是向心加速度大小与半径大小成正比和成反比问题的理解；三是从相对运动趋势方向分析水平匀速圆周运动静摩擦力方向问题.

这几个问题虽是匀速圆周运动的难点，但高一学生有强烈的求知欲，老师要比较清楚简洁引导学生突破这些难点，通过答疑来为学生解惑，在解惑过程中提升学生的物理学科核心素养，下面我就结合教学实际进行分析.

一、向心加速度的大小和方向的推导

例如图1,质量为m的质点绕o点作匀速圆周运动，线速度大小为v，半径为r，推导：

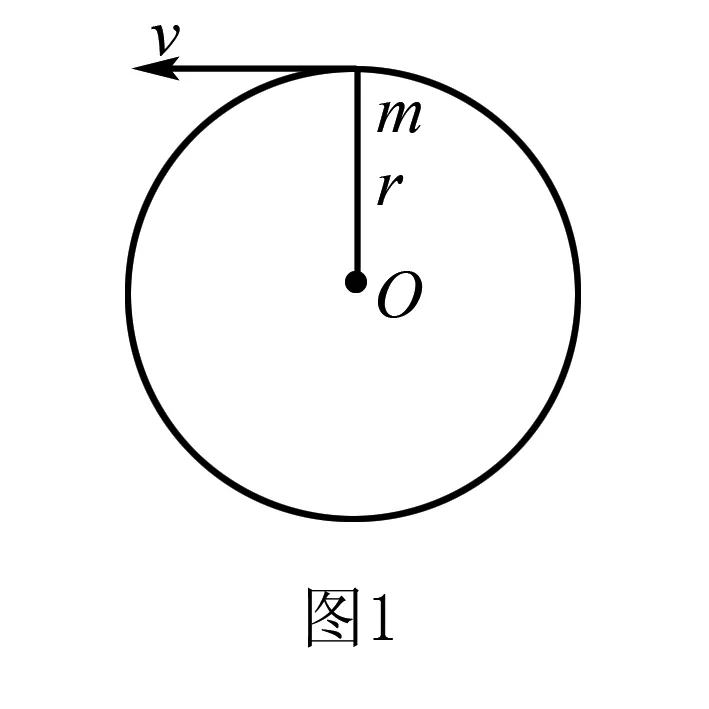
(1)向心加速度的大小;

(2)向心加速度的方向？

分析根据加速度公式a=Δv/Δt可知，向心加速度的大小等于Δt趋近于0时Δv/Δt的比值；匀速圆周运动的加速度方向通过教学,学生已知道总是指向圆心.由a=Δv/Δt可知,a的方向与Δt趋近于0时Δv的方向相同，也就是要让学生明白Δv的方向指向圆心.

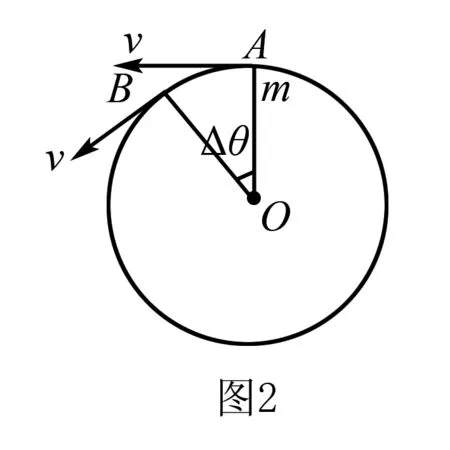
解(1)如图2，假设质点在Δt时间内由A点运动到B点，圆心角为Δθ，AB弧长SAB：

SAB=vΔt①

SAB=rΔθ②

由矢量运算法则，画出A到B速度变化量Δv的大小和方向如图3.

当Δt趋近于0时:

速度变化量大小Δv=vΔθ③

加速度大小a=Δv/Δt④

由①②③④得:a=v2/r

(2)由图3作等腰三角形底边Δv的垂线，如图4所示.

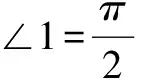
即Δv的方向与A点的速度v垂直

由于加速度a的方向Δv方向相同,可知加速度a的方向与速度v方向垂直,总是指向圆心.

二、向心加速度大小与半径大小成正比和成反比问题的理解

通过分析，最后总结：

1.某个物理量跟其他物理量有直接决定关系，那么他们之间一定有正反比关系.

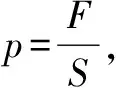
2.某个物理量是比值定义，该物理量与比值定义的两个物理量是同一物质或者同一运动的物理量，该物理量与参与定义的两个物理量没有决定关系，不能同时说成正比和成反比.

如R=U/I，不能说R与U成正比，与I成反比，因为这时U和I是理解为同一电阻的三个物理量.

3.某个物理量是比值定义，可以讨论该物理量与比值定义中一个物理量的正反比关系，但是另外一个物量必须说明不变，表示是在讨论不同物质或者不同运动的物理量的间接关联变化关系.

如v=s/t，可以说当t不变时，v与s成正比；也可以说当s不变时，v与t成反比.

再如R=U/I，可以说当I不变时，R与U成正比；也可以说当U不变时，R与I成反比.

三、从相对运动趋势方向分析水平匀速圆周运动静摩擦力方向问题

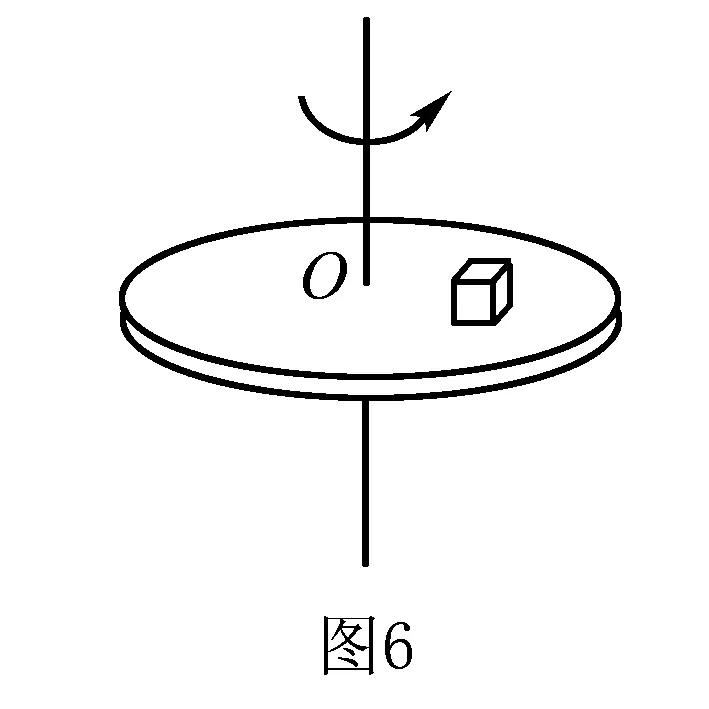
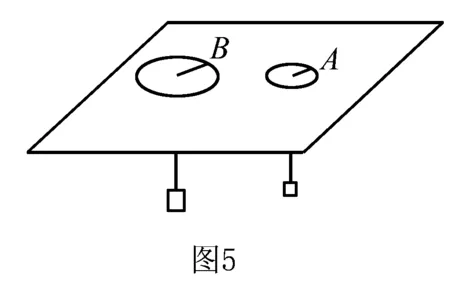
例如图6，一个圆盘绕通过圆盘的中心O且垂直于盘面的竖直轴匀速转动，在圆盘上距O点为r处放一个质量为m的物块(可看作质点)，物块随着圆盘一起做匀速圆周运动.

问：关于小物体的向心力的方向，甲、乙两人有不同意见：甲认为该向心力等于圆盘对小物体的静摩擦力，指向圆心；乙认为小物体有向前运动的趋势，静摩擦力方向和相对运动趋势方向相反，即向后，而不是和运动方向垂直，因此向心力不可能是静摩擦力.你的意见是什么？说明理由.

分析这是人教版教材必修2第五章第7节向心力配套练习中的问题之一，由物块的受力分析可知，物块受到重力、支持力、和静摩擦力，竖直方向的重力和支持力合力为零，认为该向心力等于圆盘对小物体的静摩擦力，指向圆心，因此绝大部分同学都支持甲同学的正确观点，但是这是一种间接判断的方法.进一步提问，乙同学觉得静摩擦力方向不是指向圆心，你觉得乙同学为什么错了，如何直接判断静摩擦力指向圆心呢？学生难于理解和回答！教师应该对如何根据从相对运动趋势方向相反直接判断静摩擦力指向圆心给予分析和引导.采用假设法研究，假设物块在某点突然失去静摩擦力，在Δt趋近于0时间内，物体相对圆盘的位移方向就是物体相对运动趋势方向，静摩擦力方向和这个位移方向相反.

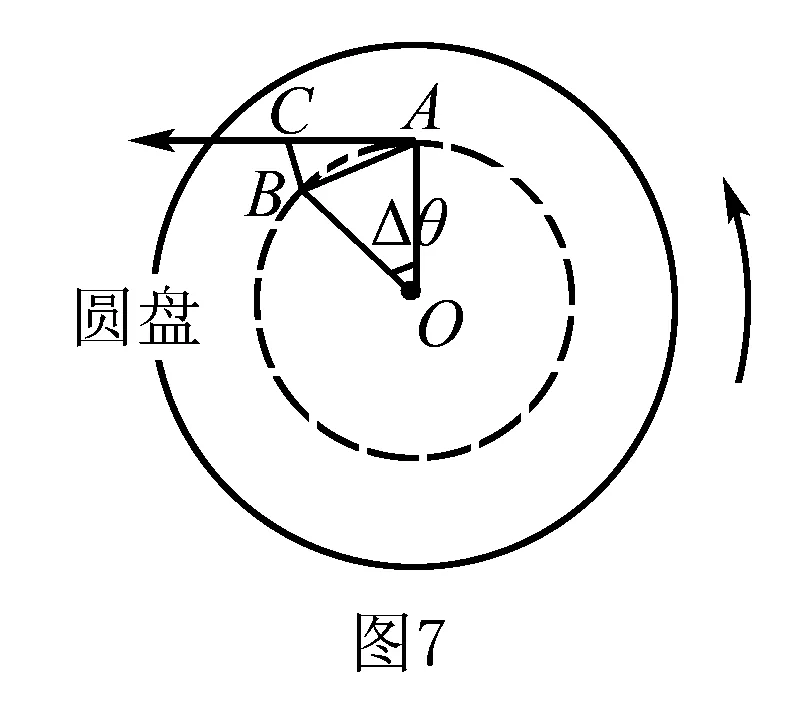
解如图7为圆盘的俯视图，假设物块在A点突然失去静摩擦力，以地面为参考系，物块将沿切线方向飞出，经过Δt时间，物块的位移大小为XAC；同时，物块开始所处的圆盘A点也运动到如图B处，物块相对圆盘的相对位移BC方向(由B指向C).

物块的位移大小为XAC：XAC=vΔt

圆盘位置A移动的弧长：SAB=vΔt

当Δt趋近于0时，Δθ非常小

可以认为线段XAB长度与弧长SAB相等， 得XAC=XAB

因此，ΔABC是一个等腰三角形

过A点作BC边垂线，可知：

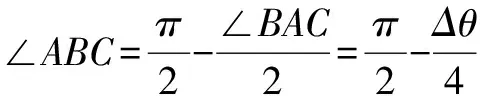
△OAB也是一个等腰三角形， 过O点作AB边垂线，可知：

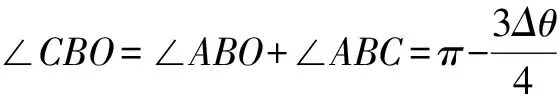
当Δt趋近于0时，Δθ也趋近于0，即：∠CBO=π

也即表示OBC在同一直线上，物块具有沿半径向外运动的趋势，因此静摩擦力方向指向圆心.