数形结合思想的应用研究
何爱贞

摘 要:实践和研究“数形结合思想的应用”,培养学生敏感、主动的“数形结合”意识,发现数学问题中的“数”与“形”,利用“数形结合”解决相关问题。“数”与“形”之间密不可分,在课堂教学中适当地利用数形结合,把握好数形结合之度,就可以使问题化难为易,化繁为简。
关键词:数形结合思想;应用研究;意义
《数形结合思想的应用研究》是我校向市级申报并立项的研究课题。两年多来课题组成员坚持采用“理论学习—课堂实践—理论提升—课堂再实践”的方式,使课题研究工作不断深入,坚持加强理论学习,积极地在课堂教学中实践,获取第一手研究资料和研究经验。
一、课题研究的现实意义
数学家华罗庚曾说过:“数缺形时少直觉,形少数时难入微。”数形结合思想可以使抽象的数学问题直观化、使繁难的数学问题简捷化,使原本需要通过抽象思维解决的问题,有时借助形象思维就能够解决,有利于抽象思维和形象思维的协调发展和优化解决问题的方法。作为一线老师,在研读教材中发现在小学数学中,特别是北师大版新教材,“数形结合”思想在很多内容中都有所渗透。“遇到问题画画图”对以直观形象思维为主的小学生来讲十分必要,但在实际教学中我们发现数学知识是一条明线,得到数学教师的重视;数学思想方法是一条暗线,容易被教师所忽视。在教授学生知识的同时很少渗透数学思想和方法,导致不少学生(学困生)解决问题的能力不强,不会灵活运用数学思想或方法,使抽象的数学问题和复杂的数学关系直观化、形象化、简单化。不能把所学的数学知识应用到实际中去。因此,根据学生的实际情况,结合我校数学课堂教学实践,确定《数形结合思想的应用研究》研究课题。
二、“数形结合”思想的应用研究实例分析
1.“数形结合”思想在“数”教学中的应用
(1)“数形结合”教学,帮助学生建立“数”的概念
“数与代数”是学习数学知识的基础,是小学阶段数学教学的重要内容。“1000以内数的认识”是学生建立“数”的概念的重要教学章节,通过这一章节的学习,学生会对“数”的概念有一个初步的认识,为进一步的数学学习打下基础。为了实现这一章节的教学目标(即认识计数单位千,发现每两个相邻计数单位之间的十进关系),笔者精心安排了三个层次的教学活动。首先,让学生数方块计数卡,在数的过程中复习对十、百的概念认识,为后面学习千的概念及相邻计数单位间的进位关系做好铺垫;当学生在计数卡中找不到1000时,适时提出问题,鼓励、引导学生将各自手中的计数卡凑在一起,尝试用别的计数单位来代替。然后老师把10张100为单位的计数卡拼加在一起,在黑板上摆出1000。当1000个小方块出现在黑板上时,这种直观的形象会在学生脑海中迅速形成一个重要的结论,那就是10个100等于1000。最后,借助电脑课件,向学生演示由1到10、由10到100、由100到1000的过程,随着电脑图形的变化,学生通过数形结合这种方式将学到的知识进行了梳理,初步建立起“数”的概念。电脑课件的时间并不长,但形象生动,起着画龙点睛的作用。
(2)通过“數形结合”向学生阐明算理
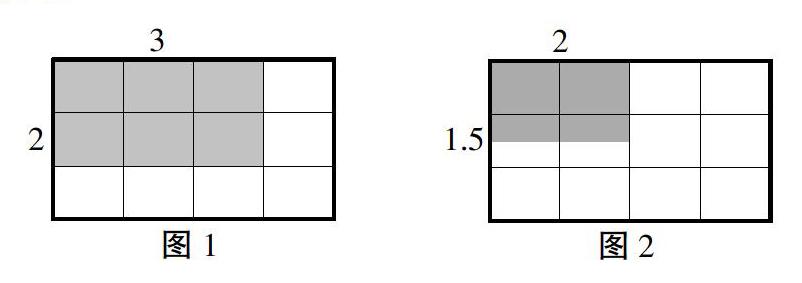
在教学实践中我们发现,对于计算教学,很多课堂教学的重点都放在了计算方法上,忽视向学生进行算理的阐明,其结果是造成学生只会机械地计算而不明其理,这对于学生在数学学习上的长远发展是十分不利的。而之所以忽视算理,一个重要的原因就是算理的抽象性,理解起来有一定的难度。基于此,运用“数形结合”的方式来进行算理的阐明,不失为一种有效的方法。利用数形结合的方式,以直观形象的算理演示,帮助学生更好地理解。如在“小数乘法”的教学中,以求算阴影部分长方形的面积为引,通过数形结合的方式向学生阐明小数乘法的算理。图1到图3不难理解,用数格及简单计算就可以解决,但对于图4中2.7×0.8这个问题,数格显然并不精确,需要通过计算的方式来进行,由此引出章节学习重点,其中的算理也不言自明了。
2.“数形结合”思想在“形”教学中的应用
数形结合,使抽象难懂的“形”一目了然。小学数学教材中,“形”的学习从一年级到六年级都有安排,小学低段数学注重“形”的直观感知即可,其实到了小学中高段数学就已经把“形”与“数”紧密联系起来了。用代数(算术)方法解决几何问题。如角度、周长、面积和体积等的计算,通过计算三角形内角的度数,可以知道它是什么样的三角形等等。再如求长方形、正方形、圆等平面图形的周长与面积,求长方体、正方体等立体图形的表面积与体积。
如,教学“三角形边的关系”一课时,老师选用画在透明胶片上的16cm长的线段作为学生探究的学具。学生每人一条胶片,剪三段后(整厘米数),有的能够围成三角形(4、5、7;2、7、7),有的不能围绕成三角形(4、3、9;3、5、8;4、4、8),多种情况的出现为后面总结三角形边的关系提供了充足的数据。而后老师在处理“两边之和等于第三边”时,对4、4、8这种情况给予足够关注,学生通过对数据的分析,很容易理解“两边之和等于第三边围不成三角形”,进而得出“三角形任意两边之和大于第三边”的规律。“形”虽然具有直观形象的优势,但是也有烦琐粗略不便于表达的劣势。要知道一些图形的特点,或者对于几何图形性质的判断,都需要通过计算才能得到正确的结论。例如,要比较两个周长相等的正方形、长方形面积的大小,凭直观地观察图形难以判断,但通过具体计算就能够一目了然。
3.“数形结合”思想在“解题”教学中的应用
(1)数形结合,化抽象为直观,从容解决问题
如“鸡兔同笼”一课,研究发现大部分教学以假设法为主,或假设全是鸡,或假设全是兔,然后引导学生直接套用公式解决问题,结果除了一部分优生外,其余学生听得一头雾水。我们课题组成员苏小英老师在执教一课中,就充分运用“数形结合”来帮助学生解决这类问题。问题“已知鸡和兔一共有10只,一共有32条腿,求鸡兔各有几只?”出示后,如果用算术方法来解决这个问题,部分学生不能理解,然而借助画图的方法,用圆表示10只动物。假设全是鸡,则每只鸡有两条腿,把腿画出,只有20条腿,但还有32-20=12条腿没画。如果每只再添2条腿,这样还得添12÷2=6只,得出兔子有6只,鸡有4只。如果每只再添2条腿,这样还得添12÷2=6只,得出兔子有6只,鸡有4只。在类似的教学中,可以让学生画图等“直观图”形式,通过借助直观图这种“数形结合”的方式来使得看似抽象的问题直观化,符合小学生以具体思维为主向抽象思维过渡的思维特点,从而让解决问题变得轻松自如,且保护学生的学习信心,激发学生的学习兴趣。
(2)数形结合,把形式多样的实际问题变成条理清晰的数学问题
小学生由于生活经历少,在遇到一些没有亲身经历过的实际问题时,往往没有办法把它们很好地转化为数学问题。教师在教学一些比较复杂的实际问题时,就要学会根据教学内容的实际情况,适时地引导学生通过画图来理解题意,表示数量关系,在自己动手作图的过程中,建立出问题的表象,从画图中去直观地体验领悟。
小学低年级的排队问题,经常出现两种不同的题型:一种是类似于从右边数起,小明排在第5个,从左边数起,小明排在第4个,这一排一共有多少人?另一种是小明的前面有5个人,小明的后面有4个人,这一排一共有多少个人?两个问题乍一看好像差不多,但其实问题中小明被算了2次,问题二中小明没有计算在内。很多学生解决问题时往往只知道用题目中出现的数字去计算,于是两题的解法都变成5+4=9。这时教师就可以适时地引入数形结合思想,教学生学会画简单的图形,把排队的这个实际问题画到自己的本子上,学生就能很直观地感受到自己的算法问题出在哪里了。
总之,在实际教学中,“数”辅助“形”,可以将“数”形象化;“形”辅助“数”,可以使“数”直观化。数形结合思想以它独有的优势在小学数学的各个阶段、各个研究领域发挥着非常重要的作用。如果每位教师都能做数学教学的有心人,充分地挖掘出每册教材中可以渗透“数形结合思想”的每个内容,再有意识地对学生加以引导,充分展示出“一图抵百语”的优势,把数形结合思想落到实处,不仅能为小学数学的发展开辟出更广阔的天地,更能让小学数学课堂充满乐趣,使每一位学生由怕数学的“矮子”变成爱数学的“巨人”。
参考文献:
吴正宪,武维民,范存丽.听吴正宪教师评课[M].华东师范大学出版社,2012-09.
编辑 王彦清

