基于FAR(1)模型的PM2.5 浓度预测研究
李气芳, 马 翠
(1.闽南师范大学数学与统计学院,福建漳州363000;2.漳州第一职业中专学校,福建漳州363000;3.数字福建气象大数据研究所,福建漳州363000)
随着我国经济的高速发展、城市化进程的加快和工业规模的扩大,以PM2.5为首的大气污染物对公众健康构成巨大威胁,不仅影响到人们的日常生活,还影响到未来的可持续发展,引起国家和社会的普遍关注.如今,我国经济发展由高速发展转向高质量发展,生态环境保护成为重中之重.在此背景下,深入研究PM2.5浓度变化的内在规律和动态趋势势在必行,这对日后的空气治理具有一定的指导意义.
国内外学者已经对PM2.5的特征规律及预测分析做了一些研究.Lu H C 等[1]使用三个不同分布分析PM2.5、PM10 和风速之间的关系.黄德生等[2]研究京津冀地区控制PM2.5污染的健康效益评估.徐小丽[3]运用主成分分析法探讨西安市及伦敦市的空气质量监测指标中多种污染物与PM2.5的相关性.Lin G 等[4]研究PM2.5浓度的空间变化关系.杨锦伟等[5]年提出基于灰色马尔科夫模型的平顶山市空气污染物浓度预测.但这些研究,都是基于离散观测数据来研究的.事实上,PM2.5小时浓度数据具有函数的特征,所以可以利用近年来流行的函数型数据分析(FDA)方法来研究[6-7].朱建平等[8]利用函数型主成分分析中国股市波动情况.严明义[9]利用函数型数据分析方法分析了网上拍卖竞买者出价水平的动态演变模式.Kokoszka P 等[10]、Park J 等[11]考虑到金融数据的自相关性,利用函数自回归模型对收益率曲线和GBP/USD 汇率曲线进行了预测分析.而每天的PM2.5浓度数据就是时间序列数据, 类似于金融数据,PM2.5浓度数据之间也具有一定的相关性,把每天的PM2.5浓度观测值看成一个函数样本,可以借助函数自回归模型对PM2.5浓度进行预测研究.
本文除利用函数重构理论和函数主成分分析方法分析漳州市PM2.5浓度数据的基本特征外, 还首次利用Bosq[12]提出的函数自回归模型FAR(1)对PM2.5浓度进行建模及样本外短期预测,希望能为决策者提供参考.
1 FAR(1)模型
FAR(1)模型,即一阶函数自回归模型,由Bosq[12]于2000 年在其专著中首次提出.该模型类似于AR(1)模型,但因为变量是函数,所以估计方法大有不同.在利用FAR(1)模型之前,先把观测到的离散数据重构成函数曲线,再对函数曲线族进行FPCA 分析得到有限的K 个函数主成分,从而可以估计出FAR(1)模型中的算子,最后进行短期预测.
1.1 函数重构
在函数型数据分析中,假设数据是由一个函数过程产生的,但是现实中,我们能够观测到的数据仍然是离散的,所以在进行函数型数据分析之前,首先要利用平滑技术将观测到的离散数据重构成连续取值的函数型数据.重构函数曲线的方法很多,本文采用的是带有惩罚项的基函数法.
假设观测到的数据是{(yj,tj),j=1,2,…,N},服从的模型是 yj=x(tj)+j,重构的函数 x(t)可以利用基系统中的基函数(t)的线性组合来估计,即.利用残差平方和最小准则,有
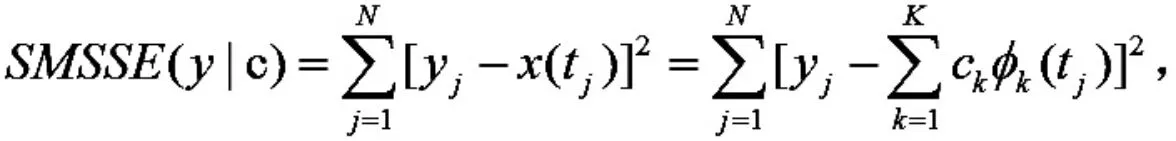
为平衡重构函数曲线的拟合度和粗糙度,在重构函数时,加入惩罚项.曲线的粗糙度通常用函数二阶导数的平方的积分(Dx(t)表示函数 x(t)的导数)来衡量,那么对应的带惩罚项的残差平方和为
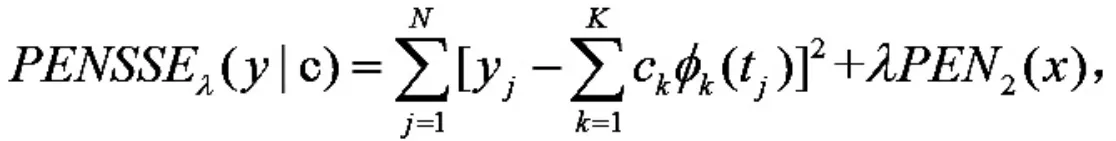
函数进行重构后,可以求出均值函数曲线和样本方差-协方差曲面
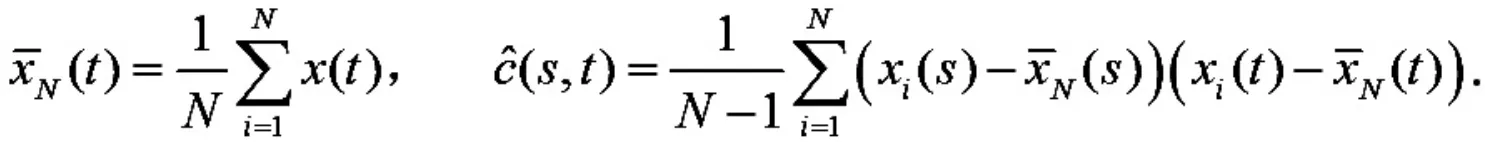
1.2 函数主成分
对观测到的离散PM2.5浓度数据进行重构后, 接下来把每条函数曲线当作样本进行函数主成分分析.在Ramsay[6]的专著中,一元函数主成分权函数 ξ(t)对应经典多元回归分析中的权向量,第i 个样本曲线在第k 个主成分上的得分定义为
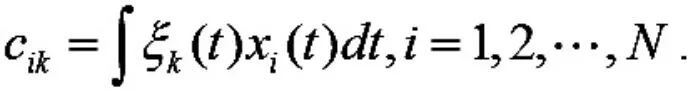
那么第一主成分权函数ξ1(t)可以通过最大方差求解得到:
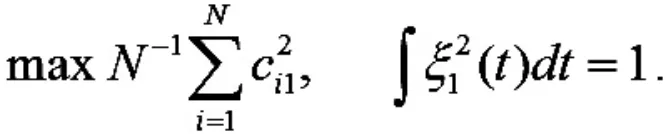
同理,第j 主成分权函数可以求解得到:
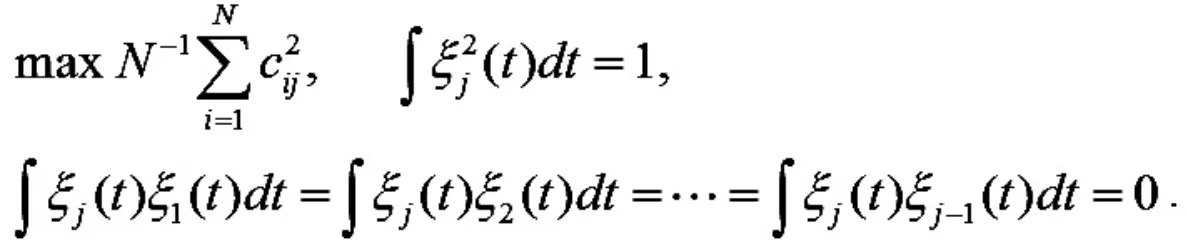
1.3 FAR(1)模型及预测分析
假设函数曲线 x1(t)在Hilbert 空间连续可积, A 是 Hilbert-Schmidt 算子,i(t)为函数型白噪声序列.则 FAR(1)模型如下
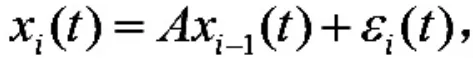
引入自相关函数
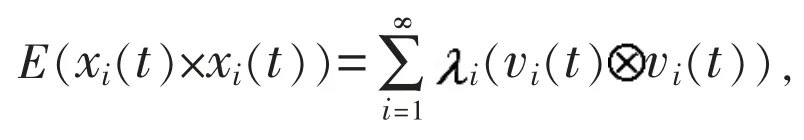
根据自相关函数,可定义偏自相关函数:

2 FAR(1)模型在PM2.5 浓度预测中的应用
2.1 数据说明与特征描述
本文所用的是2017 年11 月1 日至2018 年5 月5 日漳州市的PM2.5小时浓度数据,来自中国环境监测总站的全国城市空气质量实时发布平台.在进行FAR (1) 模型预测分析时,2017 年11 月1 日至2018 年4月30 日PM2.5小时浓度数据作为样本,2018 年5 月1 日至5 月5 日PM2.5小时浓度数据作为预测对比.
利用R 软件,利用广义交叉验证(GCV),得到最优的Fourier 基底个数为11,惩罚参数lambda=0.5.利用带有惩罚项的基函数法把PM2.5小时浓度数据重构成函数曲线, 利用前面介绍的公式得到均值变化曲线和方差-协方差曲面.
从图1 可以看出,每天的PM2.5浓度曲线是随机波动的,部分异常曲线值远远大于总体均值,说明那些天污染非常严重.
从图 2 可以看出,2017 年 11 月 1 日至 2018 年 4 月 30 的 PM2.5浓度均值在 40 左右,2017 年 11 月、2018 年 1 月、2 月和 3 月的 PM2.5浓度均值稍低于总体均值,2017 年 12 月和 2018 年 4 月的 PM2.5 浓度均值稍高于总体均值,说明这两个月污染比较严重.另外,从均值曲线变化趋势可以看出,下午时段的曲线有下降趋势,说明该时段污染比较轻.
从图3 可以看出函数曲线上时间点s 和t 之间的相关性.正对角线数值都比较大,说明同时间点之间的相关性最强;副对角线数值较小,且呈现下降趋势,说明时间点之间的距离远大,相关性越弱;这些特点跟实际是相吻合的.

图 1 漳州 2017 年 11 月1 日至 2018 年 4 月 30 日 PM25 浓度变化曲线Fig.1 The variation curve of PM2.5 concentration in Zhangzhou from November 1, 2017 to April 30, 2018
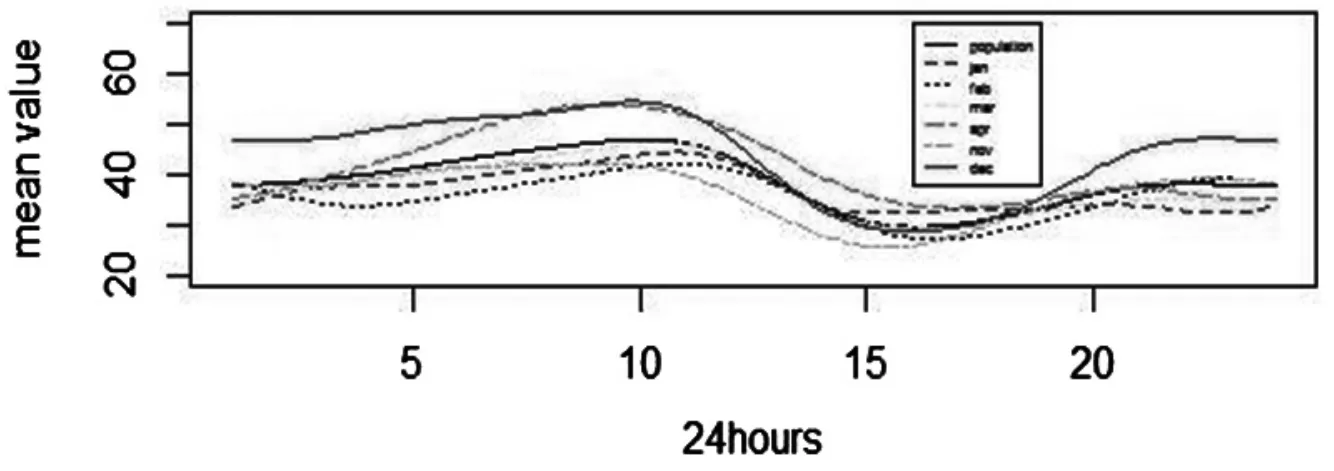
图2 总体的PM2.5 浓度均值变化曲线和每个月的PM25 浓度均值变化曲线Fig.2 The population mean curve and the monthly mean curve of PM25 concentration
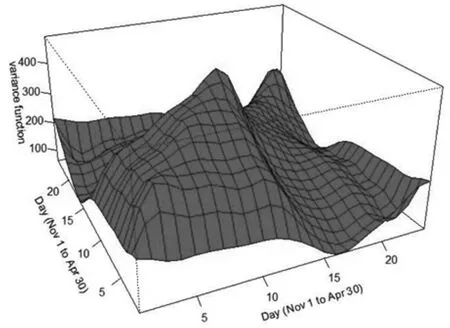
图3 函数曲线上时间点s 和t 之间的方差-协方差曲面Fig.3 The variance-covariance surface between the time points s and t on the function curve
2.2 PM2.5 浓度的函数主成分分析
函数重构后可以进行函数主成分分析.利用R 软件, 结果显示前3 个函数主成分的方差累积贡献率达到90.3%, 体现最主要的变异方式, 其对PM2.5 变异的解释能力分别是67.2%、14.0%和9.1%.图4是前3 个函数主成分偏离均值曲线的效果图.
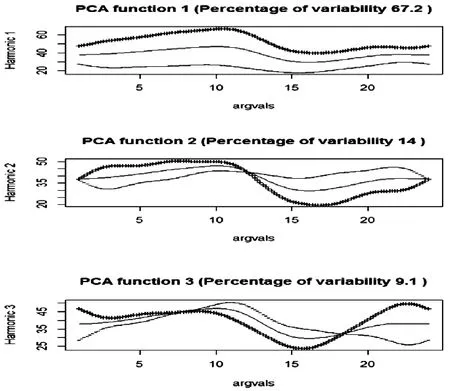
图4 前3 个函数主成分偏离均值的效果图Fig.4 The effect diagram of the first three function principal components deviate from the mean
从第一主成分函数曲线形状可以看出,整条曲线基本没有波动,说明第一主成分代表的是PM2.5浓度在一天中比较平稳的特征.第二主成分函数曲线像是一条正弦曲线, 代表PM2.5浓度在下午13 点前后波动较大, 而且13 点之前是正向效应;13 点之后是反向效应.从第三主成分函数曲线可以看出,PM2.5浓度上午比较平稳,下午出现较大的反向效应,晚上出现较小的正向效应.
2.3 FAR(1)模型预测结果分析
利用Matlab 软件,通过函数主成分投影法对FAR(1)模型中算子进行估计,然后做1 步向前预测,得到2018 年5 月1 日至5 月3 日的PM2.5浓度曲线及对应的小时浓度值,并与真实值进行比较.
从图5 看出,2018 年5 月1 日预测值曲线比实际值曲线稍微偏大,但整体趋势比较相近;后面几天的预测曲线与实际值曲线趋势不尽同,个别时刻变化波动较大,这可能是因为PM2.5浓度它受风向、地域、污染物排放等复杂因素影响,每天的不同时间点的浓度值差异较大,且变化较快.另外,每天的观测值只有24 个,频率较低,函数特性表现不完整,导致函数重构出现偏差,可加大每天的观测样本.
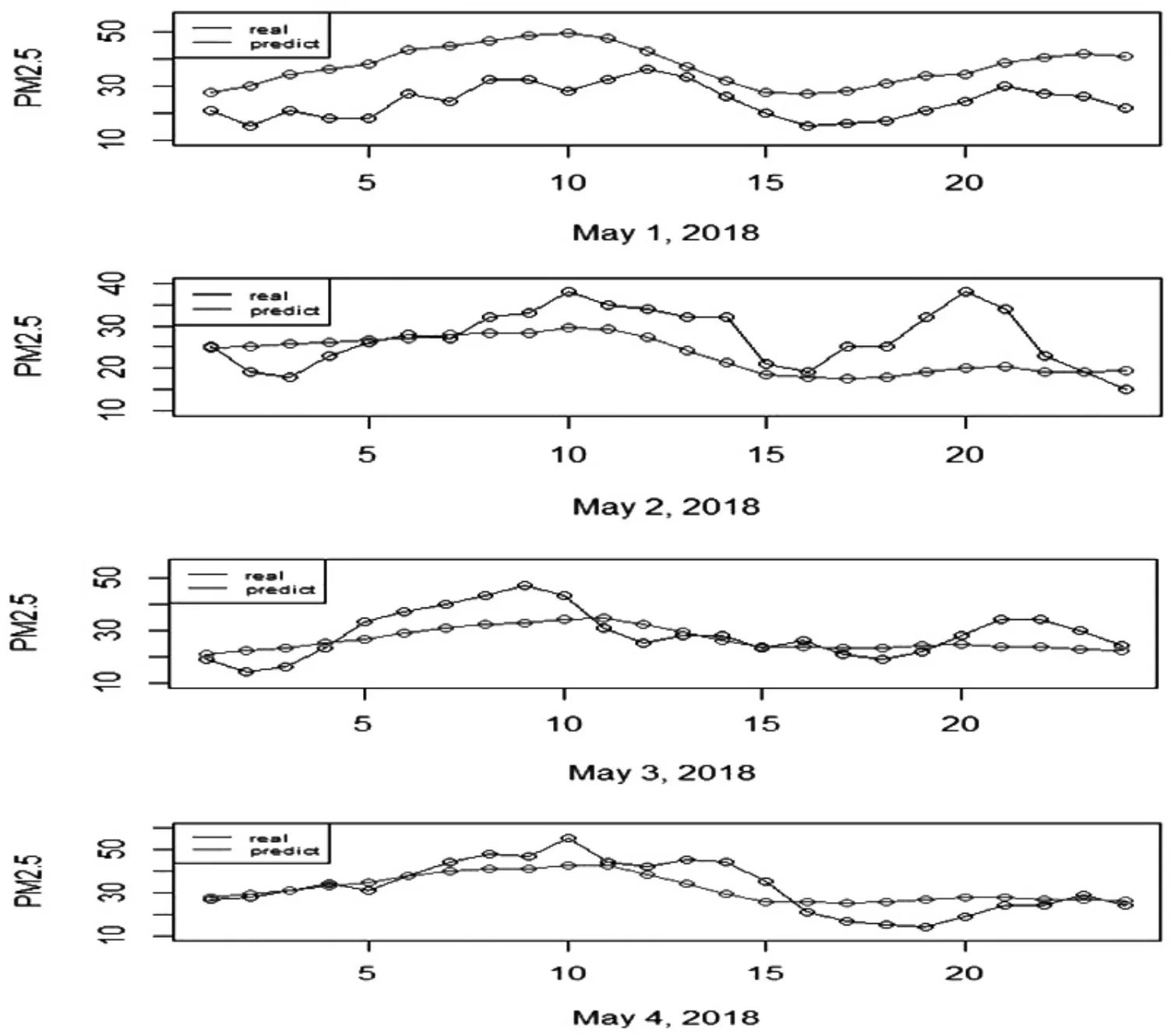
图5 漳州2018 年5 月1 日至5 月5 日PM2.5 浓度预测值与真实值对比图Fig.5 Comparison of predicted and true values of PM2.5 concentration from May 1 to May 5, 2018 in Zhangzhou
3 结论
文中利用函数型数据分析方法对漳州市2017 年11 月1 日至2018 年5 月5 日的PM2.5小时浓度数据进行了研究.通过对PM2.5小时浓度数据的函数重构,描述出其函数特征,并得到函数均值曲线和方差-协方差曲面.通过对函数曲线进行函数主成分分析表明前3 个主成分的方差累积贡献率达到90.3%, 综合PM2.5浓度曲线的最主要变异方式.通过对PM2.5浓度曲线进行函数自回归分析及短期预测,预测效果相对较好.

