带自环的无向网络的同步研究

孔秀琼，袁正中,2,3, 蔡 萍,2,3

（1.闽南师范大学数学与统计学院,福建漳州363000；2.数字福建气象大数据研究所,福建漳州363000；3.数据科学与统计学重点实验室，福建漳州363000）

复杂网络是科学研究中的一个重要课题[1]，有大量科研人员进行研究，得到了丰富研究成果，特别是网络结构[2]、网络动力学系统[3]和网络控制[4].同步是一个广泛存在的自然现象，最早由丹麦物理学家惠更斯[5]发现，到20 世纪90 年代，同步研究的重点为混沌系统的同步[6].随着复杂网络的兴起，复杂网络的同步[7]成为动力学系统的一个研究热点.我们大体可以把复杂网络的同步研究分为3 种:自同步、控制同步和同步识别.复杂网络的自同步是研究网络在同步情况下，网络的拓扑结构对同步性能的影响，包括哪种网络同步性能最好[8]，如何改变网络的拓扑结构使网络同步性能最好[9]和网络结构对网络同步性能的影响[10]等.控制同步主要通过不同的控制方法使网络达到同步，例如线性反馈控制[11]、自适应控制[12]和牵制控制[13]等.同步识别是利用网络的同步识别网络的拓扑结构[14].然而，这些研究都有一个重要前提：网络都是无自环的.但是，在一般的生物网络[15]、电力网络[16]以及社会学动力系统[17]中自环是普遍存在的，对网络同步有重要影响.本文讨论具有部分自环和全自环两种情形的无向网络的同步问题，首先，利用Lyapunov 稳定性方法研究网络在部分自环和全自环网络两种情况下的同步态、同步准则和同步性能，在理论上说明自环对网络同步的作用，然后通过数值仿真验证了相关结论.

1 带自环无向网络的动力学系统

对于含N 个相同节点的网络[5-6]，其中第 i 个节点的状态方程为：

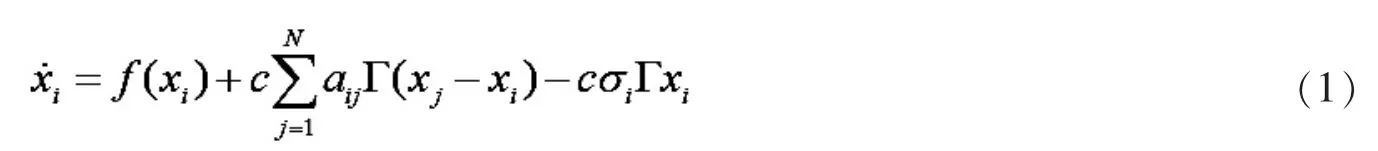
1.1 部分自环网络

1.1.1 同步态

当网络节点没有全部加自环（存在σi≠1）时，如果动态网络式（1）达到同步，则变量满足

当网络达到完全同步时，xi-xj=0.此时等式（1）右端的第二项等于0，动态网络变成

显然，由于网络存在部分自环，系统（3）同步态为

1.1.2 稳定性分析

对等式（1）关于同步状态0 附近进行线性化，得到如下方程

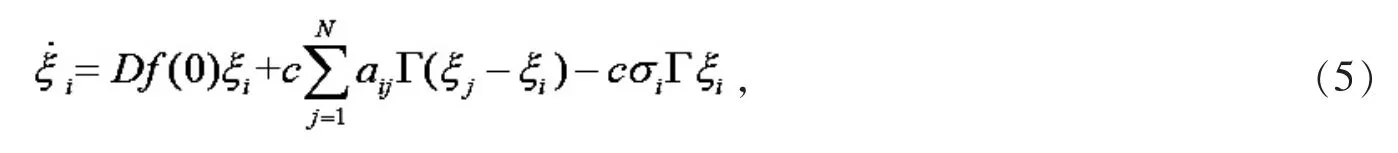
这里 Df（0）是 f（0）关于同步状态 0 的 Jacobi（雅可比）矩阵，令，可以得到

由于矩阵 A 对称不可约以及 σ 为对角矩阵， 存在可逆矩阵 S 满足 A-σ=SΛS-1， 其中 Λ=diag是矩阵 A-σ 的特征值，且令 η=［η1，η2，…，ηN］=ξ［ξ1，ξ2，…，ξN］S.

则有

（7）式等价于

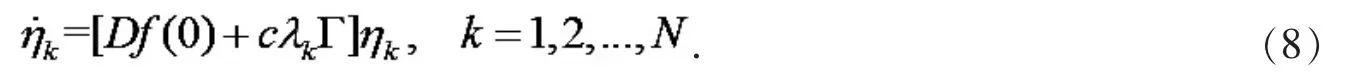
动态网络式（1）的稳定性转变成线性方程（8）的稳定性.由文献[18]可知，当存在一个常数α＜0 使得是Hurwitz 稳定矩阵，并且耦合强度满足如下条件

1.2 全自环网络

对于含N 个相同节点的网络[5-6]，其中第 i 个节点的状态方程为

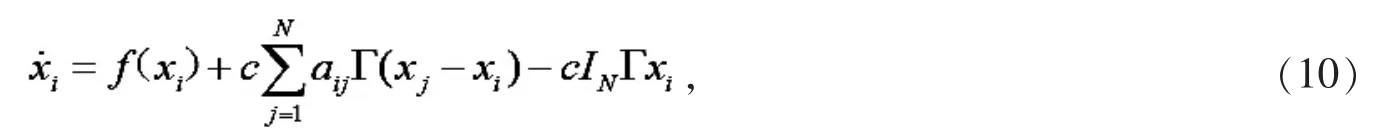
式（10）中，各个变量代表的含义与（1）式相同.

1.2.1 同步态

当网络全加自环（σ=IN）且达到同步时，

此时等式（10）右端的第二项等于0，动态网络变成

由于耗散耦合条件，同步状态s∈Rn必为单个孤立节点的解，即这里s 的形态多种多样.所以，当网络全加自环时，系统（10）同步态不唯一.

1.2.2 稳定性分析

对状态方程式（10）关于同步状态 s 线性化，令ξi=xi-s，得到如下方程

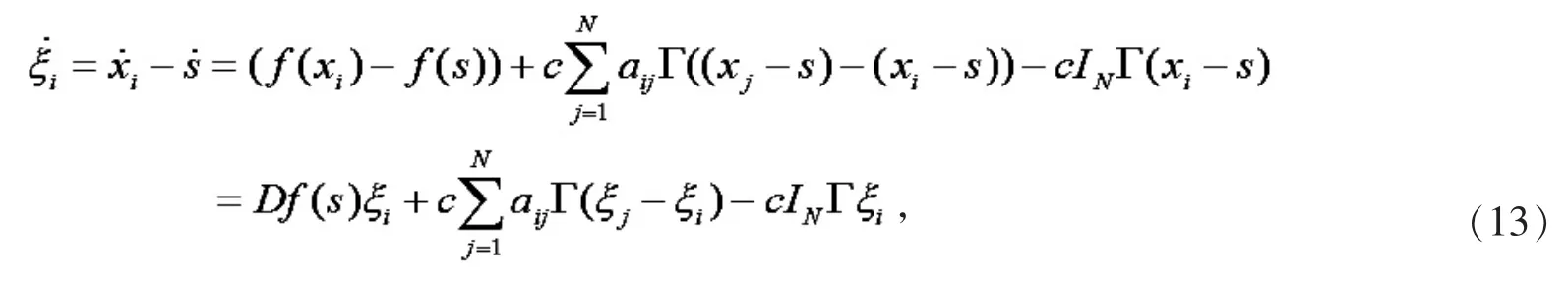
这里 Df（s）是 f（s）关于同步状态 s 的 Jacobi（雅可比）矩阵，令 ξ［ξ1，ξ2，…，ξN］，则

记 A-σ=SΛS-1为矩阵A 的Jordan 分解，这里假设 Λ 为对角矩阵，即由于网络为全自环网络，所以矩阵A-I 的特征值k=βk-1，这里 βk为矩阵 A 的特征值.再令 η=［η1，η2，…，ηN］=ξS，则有

式（15）等价于

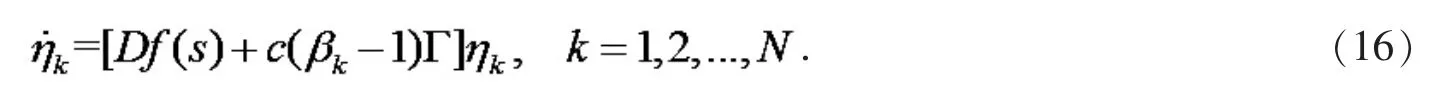
动态网络式（10）的稳定性转变成线性方程（16）的稳定性.由于矩阵A 为不可约矩阵，其特征值为所以，矩阵 A-I 的最大特征值为-1.当存在一个常数 α＜0，使得［Df（S）+αΓ］是Hurwitz 稳定矩阵，并且耦合强度满足如下条件

则带自环的动态网络式（10）能达到完全同步.

2 数值模拟

以下仿真考虑当网络在 f（x）为Lorenz 系统的同步情况，为简单起见，令Γ 是单位矩阵.所有网络的仿真以变量 x2为例，图a 至图 d 中横轴为同步时间，纵轴为状态变量 x2的值.

1) 考虑含200 个节点的BA 无标度网络（m=3）和ER 随机网络（p=0.3），耦合强度为40 时，网络的同步情况如图1 所示.

图1 BA 无标度网络和ER 随机网络的同步情况Fig.1 Synchronization of BA scaleless network and ER random network

图1 中横轴为时间，纵轴为变量 x2状态轨迹.a 为无自环BA 无标度网络，c 为无自环ER 随机网络，由于变量 x2状态轨不一致， 网络无法达到同步；b 为添加60%自环后的BA 无标度网络，d 为添加60%自环后的ER 随机网络，由于变量 x2状态轨迹都趋于0，网络达到同步状态.

2) 同等网络规模（N=200）全自环网络的拓扑结构，决定了即使耦合强度不大，网络也可以达到同步.考虑全自环的BA 无标度网络和ER 随机网络，耦合强度为28 时，网络的同步情况如图2 所示.

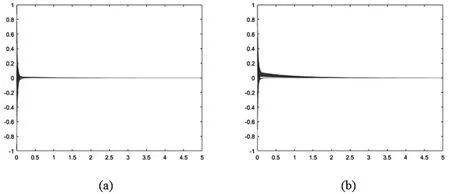
图2 全自环BA 无标度网络和ER 随机网络同步情况Fig.2 Synchronization of All-Self-Loop BA scaleless network and ER random network

图2 中横轴为时间，纵轴为变量 x2状态轨迹.a 为全自环BA 无标度网络，b 为全自环ER 随机网络，由于变量 x2状态轨迹都趋于0，网络达到同步状态.

所以，当网络的耦合强度相同时，加入不同数量的自环，可以促进网络同步；当网络为全自环网络时，给出较小的耦合强度，网络可以快速达到同步.

3 总结

本文深入研究了带自环网络的同步问题.从理论上证明了部分自环网络和全自环网络的同步状态、同步准则和同步性能，说明了自环对网络同步的促进作用.用部分自环和全自环的ER 随机网络和BA 无标度网络验证网络同步性能随着自环数目的增加而增强.