局部对偶平坦的（α，β）-度量的共形性质

翁桂英, 林伟华

（1.仰恩大学数学系,福建泉州362014；2.闽南师范大学数学与统计学院,福建漳州363000；3.福建师范大学数学与计算机学院,福建福州350007）

设F=F（x，y）是 n 维流形M 上的芬斯勒度量，若在任何一点存在局部坐标系（xi）使得测地系数G=, 其中H=H（x，y）是TM ｛0｝上三次正齐次的光滑标量函数，则称芬斯勒度量F=F（x，y）为局部对偶平坦，并称此坐标系为恰当坐标系.芬斯勒几何中局部对偶平坦的概念最近得到比较深入的研究, 文献[3]研究了局部对偶平坦在信息几何中的应用, 文献[4]研究了对偶平坦的Kropina度量的标量旗曲率及迷向S-曲率的特征,文献[5]研究Randers 度量为局部对偶平坦的条件，文献[6]研究了局部对偶平坦且共形平坦的Kropina 度量.沈忠民[1]证明了开集URn上的芬斯勒度量F=F（x，y）为局部对偶平坦的充要条件为其满足偏微分方程：.夏巧玲[7]研究了 （α， β）-度量为局部对偶平坦的充要条件.

芬斯勒几何的共形相关在某种意义上是保角相关[2].给定流形M 上的芬斯勒度量F 和，若存在 M上的一个标量函数 c（x），使得，则 F，称为共形相关.特别如果F 共形于闵可夫斯基度量，则称F 为共形平坦.目前对偶平坦的 （α，β）-度量的共形相关性大多局限于特殊的 （α，β）-度量，本文利用文献[7]中刻画对偶平坦的 （α，β）-度量满足的方程对共形相关性的结果推广到一般的对偶平坦的（α，β）-度量，得到了下面定理.

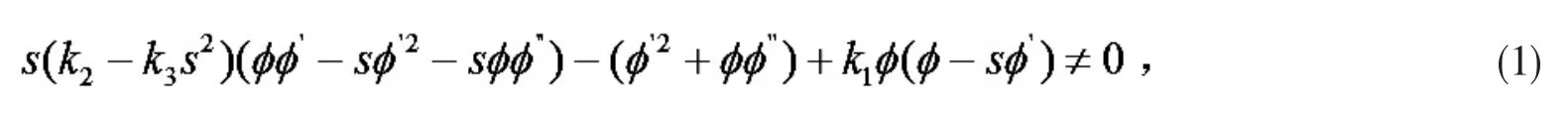
本文不特别说明均采用爱因斯坦求和约定.

1 预备知识

n 维流形 M 上（α， β）-度量有如下形式

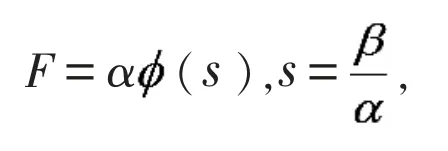
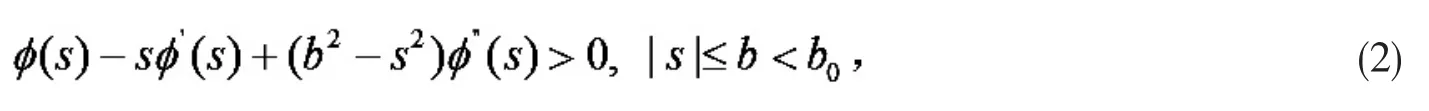
在（α，β）-度量中，为便于计算，引入如下记号

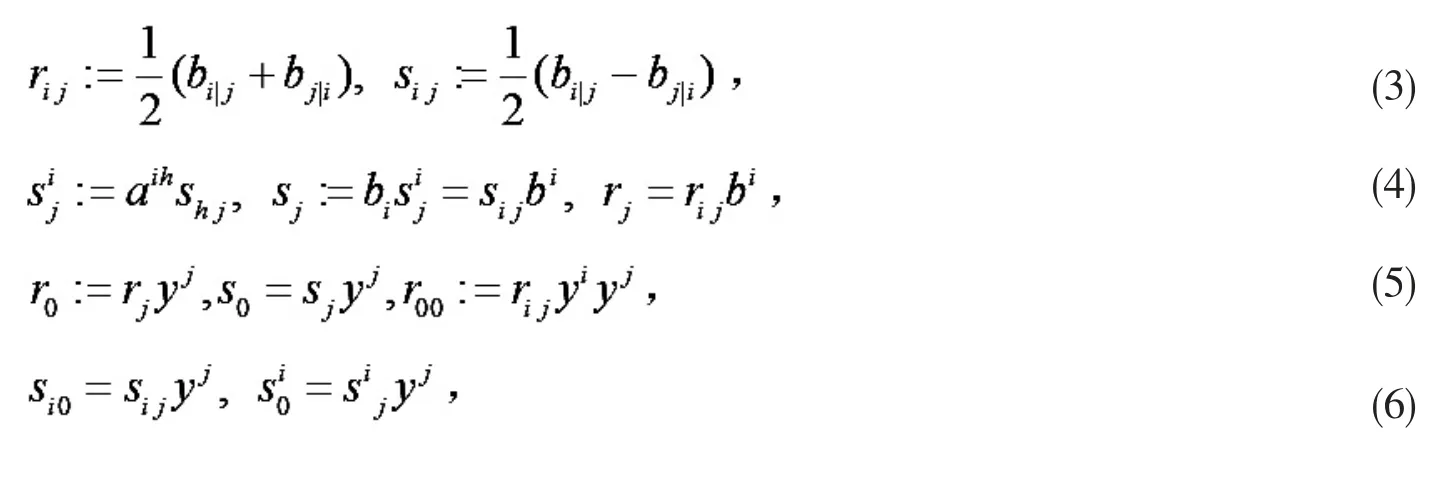
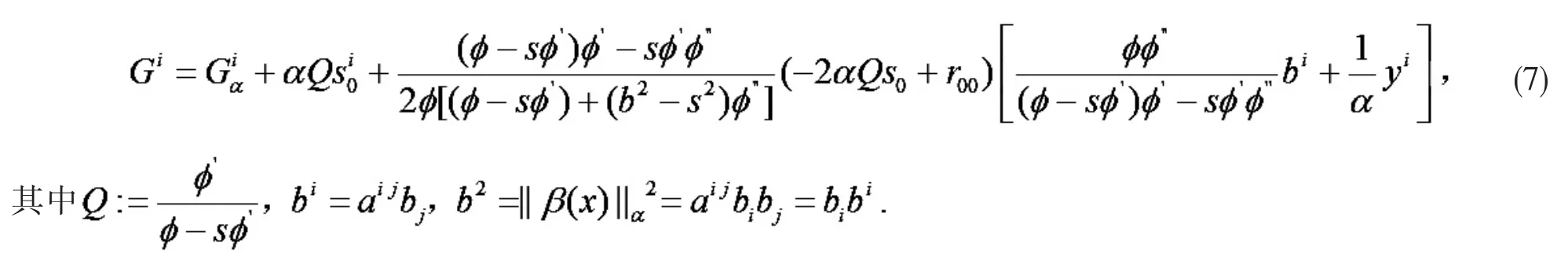
芬斯勒几何的共形性质是几何学家研究的热门问题,Weyl 定理证明了一个芬斯勒度量的共形性质和射影性质唯一地决定了这个度量的结构.对于流形M 上的芬斯勒度量F，，若满足，其中 c（x）为 M 上标量函数，则称F，共形相关.此时称标量函数 c（x）为共形因子.

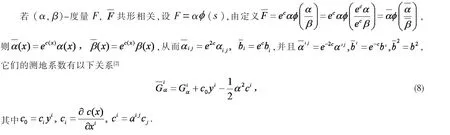
并且有

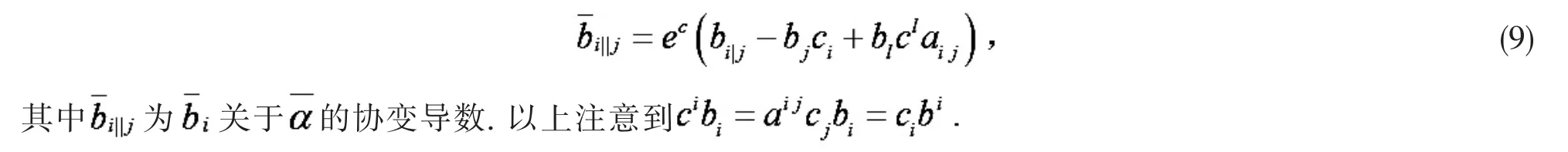
为证明结论，引入以下引理.

引理1[2]（α，β）-度量为局部闵可夫斯基当且仅当α 为平坦的，且bi│j=0.

为后文引理叙述需要引入以下记号

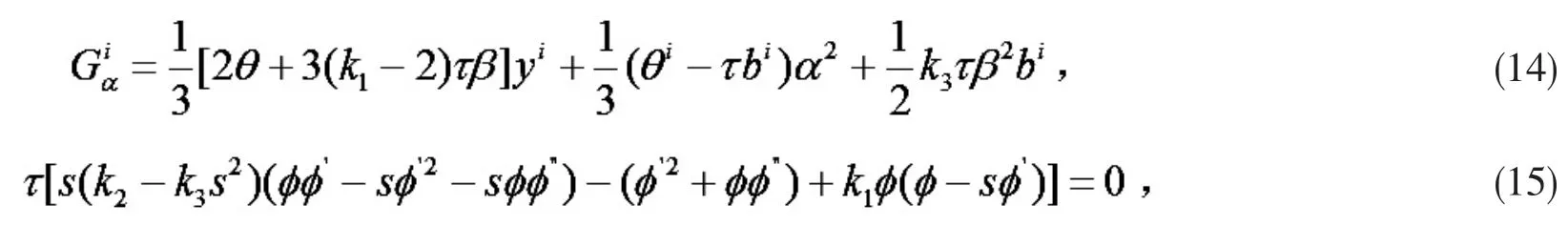
其中 k1，k2，k3为常数如式(11)定义，是标量函数，为 M 上 1-形式，θi:=aijθj.

引理 3[7]设维流形 Mn（n3）上 （α，β）-度量，假设条件同引理 2，若满足

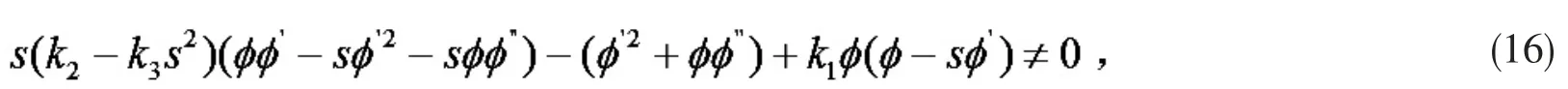
则F 是局部对偶平坦当且仅当

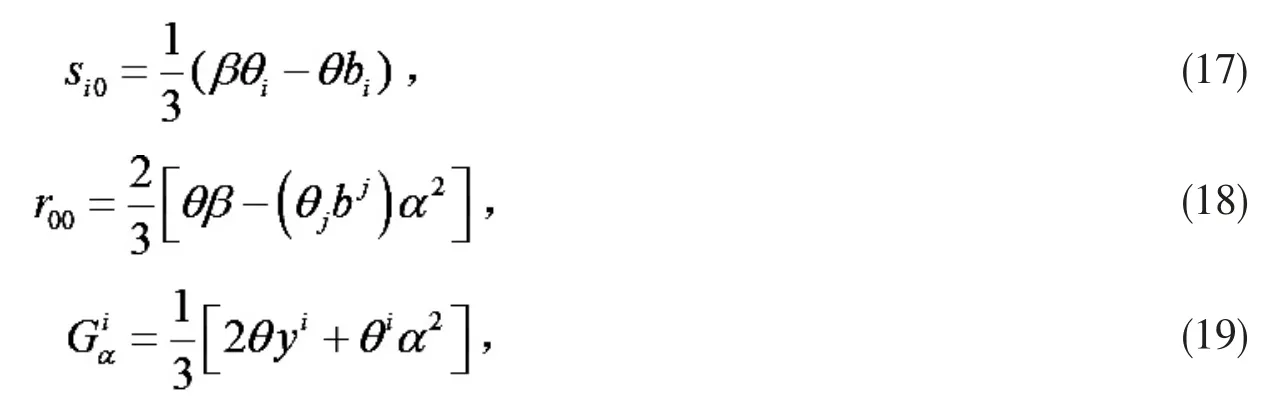
其中 k1，k2，k3及 θ 定义同引理 2.

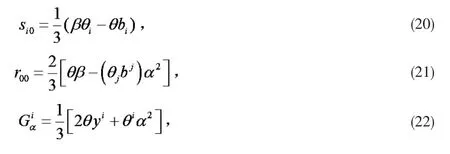
其中 k1，k2，k3及,θ 定义同引理 2.

引理 5 若 φα2=σβ，其中 α， β 定义如前， φ 为 M 上函数， σ:=σi（x）yi:=σ0为 M 上 1-形式，则φ=0，σ=0.

证明 对 M 上任意点，若 φ≠0，则 φα2=φαijyiyj为二次型，矩阵（φαij）是可逆， σβ=σibjyiyj也为二次型，其矩阵（σibj）秩为 1，矛盾，故 φ=0；从而 σibjyiyj=0，由 yi，yj的任意性，向量（bj）≠0，则列向量（σi）=0，从而 σ=0.

2 定理的证明

定理1 的证明 1)必要性.F 共形平坦，与局部闵可夫斯基度量共形相关，由引理1 有，又由式(8)(9)，

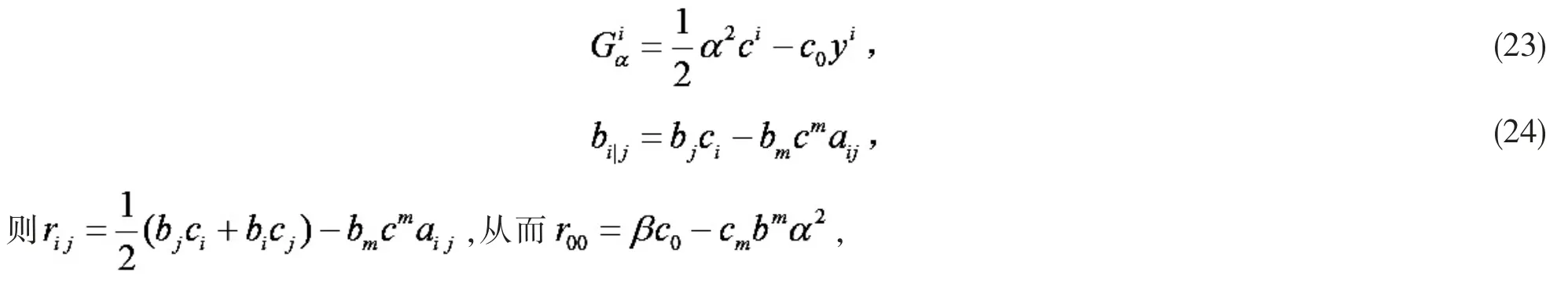
从而由引理2，

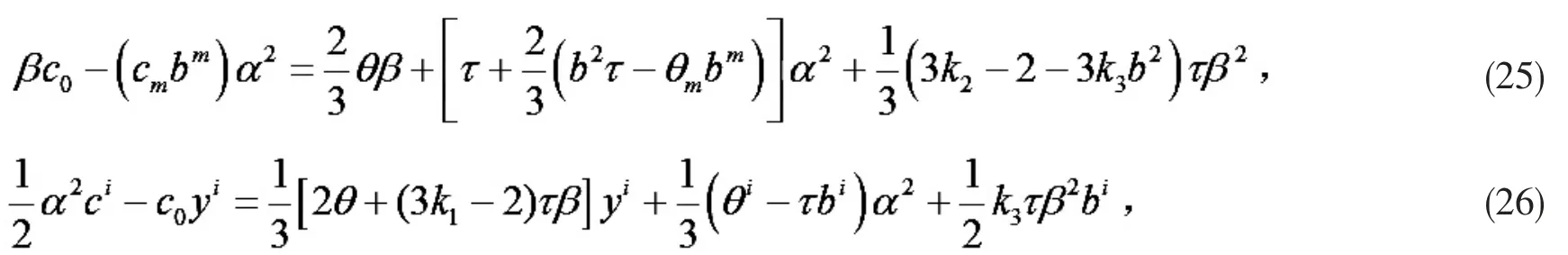
(25)式由引理5，

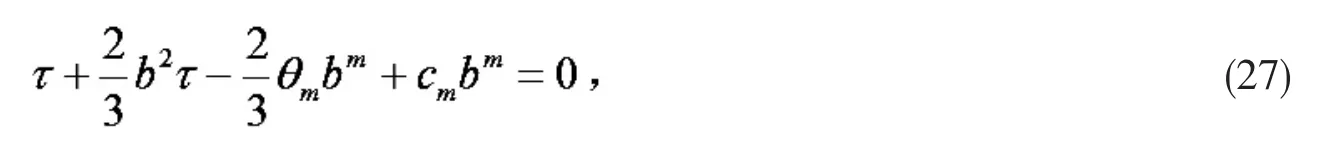
(26)式与 bi缩并得

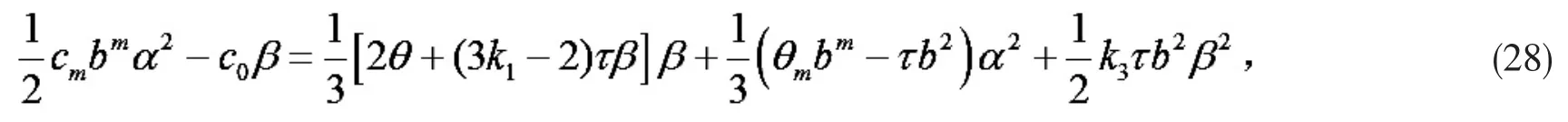
由引理5

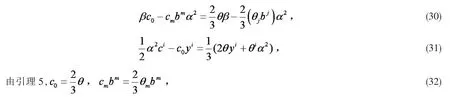
(31)式与 bi缩并得，

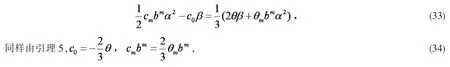
由(32)(34)式可得 c0=0，从而，c（x）为常值函数，所以F 为局部闵可夫斯基度量.

2) 充分性显然.

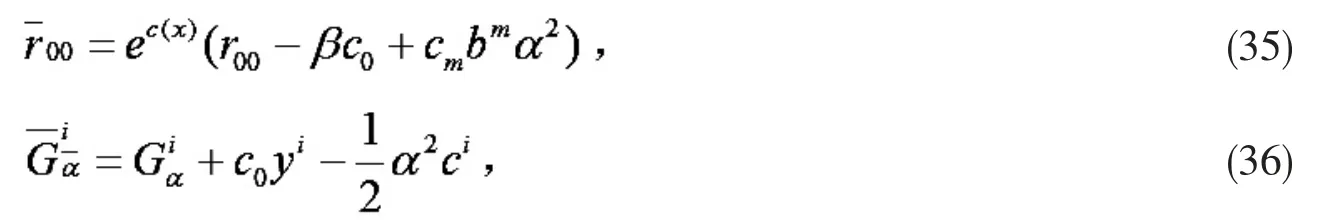
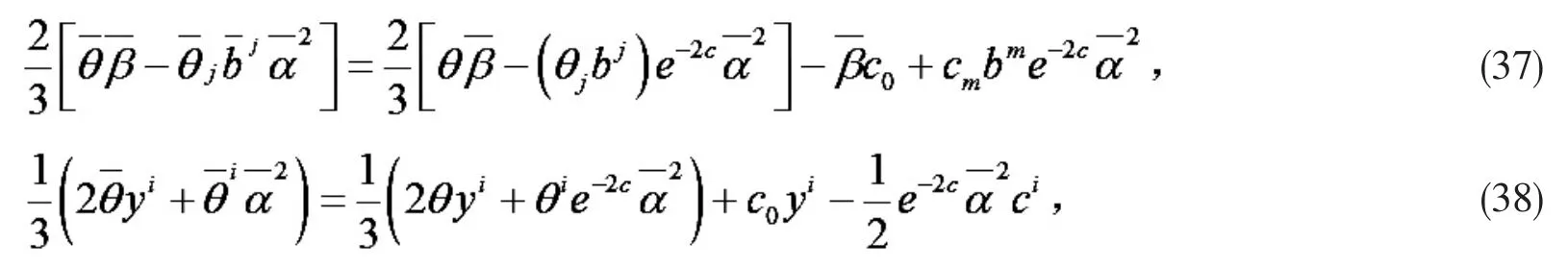
(37)式由引理5，

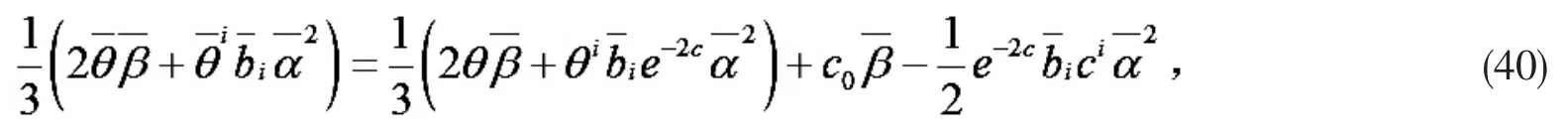
由引理5，

由(39)(41)式 c0=0，从而 c（x）为常数.

2) 充分性显然.