双HOG 特征的相关滤波目标跟踪

林淑彬

（闽南师范大学计算机学院，福建漳州363000）

视觉目标跟踪[1]是计算机视觉中的一个热点问题，涉及图像处理、模式识别、人工智能、自动控制等不同领域[2]，在安全监控、人机交互、无人驾驶、医疗诊断系统、机器人学等方面[3]有广泛应用，因此得到极大关注.视觉目标跟踪的难点在各种各样的挑战中，如局部遮挡、变形、运动模糊、快速运动、光照变化[4]、背景杂乱[5]、目标再识别和尺度变化[6]等.目前已经提出了许多跟踪算法来处理不同的对象跟踪问题，基于相关滤波器(Correlation Filter, CF)的跟踪方法[7]和基于判别相关滤波[8](Discriminative Correlation Filter, DCF)的跟踪方法因其性能优异、速度快而备受关注.

CF 主要应用于信号处理，用来描述两个信号之间的相关性，其最大的优点是计算速率高，利用假设训练数据的循环结构，目标和候选区域能在频域[9]进行表示并通过快速傅里叶变换(FFT)操作.Bolme 等[10]首次将CF 应用于跟踪提出MOSSE 算法，其利用FFT 的快速性使跟踪速度达到了600-700fps.DCF 通过跟踪训练滤波器模型中目标的位置，提取出HOG 特征，训练出一个滤波器模板，对于新的可能目标区域，提取出该区域HOG 特征，与滤波器模板作相关.重复上述步骤进行后续的目标跟踪与模型训练[6]，从而实现模型的在线训练[12]与目标的实时跟踪[13].实验表明，凭借HOG 特性，DCF 比顶级跟踪器[11]表现更加出色，能以每秒数百帧的速度运行.

由于设计满足各种挑战性场景的特征融合方法的难度很大，为了获得更好的性能，让跟踪器可以可靠地处理各种问题，跟踪器的单一性能有时会出现不稳定的情况，但是跟踪器的多种特征融合[14]可以有效地增强其鲁棒性[15].受DCF 算法的启发，本文提出一种有效的双HOG 特征目标跟踪（Dual HOG feature correction filter，DHCF）方法.该方法结合不同类型的特征，通过DCF 构造两个HOG 特征，一个是HOG1，另一个是HOG2， 接着利用判别相关滤波器框架对两个特征进行滤波处理， 使它们都各自独立地跟踪目标，然后从处理好的两个特征中选择最优特征，根据特征获得响应图，在响应图中寻找最大值位置，就是预测出的新目标位置.其相关运算在傅里叶域中使用傅里叶变换进行计算， 通过使用多维特征和改进的滤波器训练方法[18]进一步提高了性能和计算效率.

DHCF 跟踪器具有双HOG 特性，与许多复杂的跟踪器性能相当，在OTB-2013[26]、OTB-2015[27]基准上与其他算法对比取得了良好的效果.为了验证DHCF 跟踪器的性能， 通过与Staple[17]、SAMF、LCT、KCF、DSST[20]、HOG 这六个跟踪器进行了比较，图1 显示了两个基准序列上各种跟踪器的比较结果.

图1 各跟踪器比较效果图Fig.1 Each tracker comparison renderings

1 相关滤波器

本节引入相关滤波的概念， 相关滤波是用来描述信号处理领域中两个信号之间的相似程度.以下主要讨论与本文密切相关的两类跟踪器，1.1 节介绍相关滤波器，1.2 节介绍判别相关滤波器.

1.1 相关滤波器

2010 年CVPR，David S.Bolme 首次将相关滤波用在了跟踪领域[11].相关滤波目标跟踪方法的基本思想是：跟踪中的两个信号越相似，其相关值就越高，越接近所需的目标区域.实验中通过设计相关滤波模板来实现，如图2 所示.

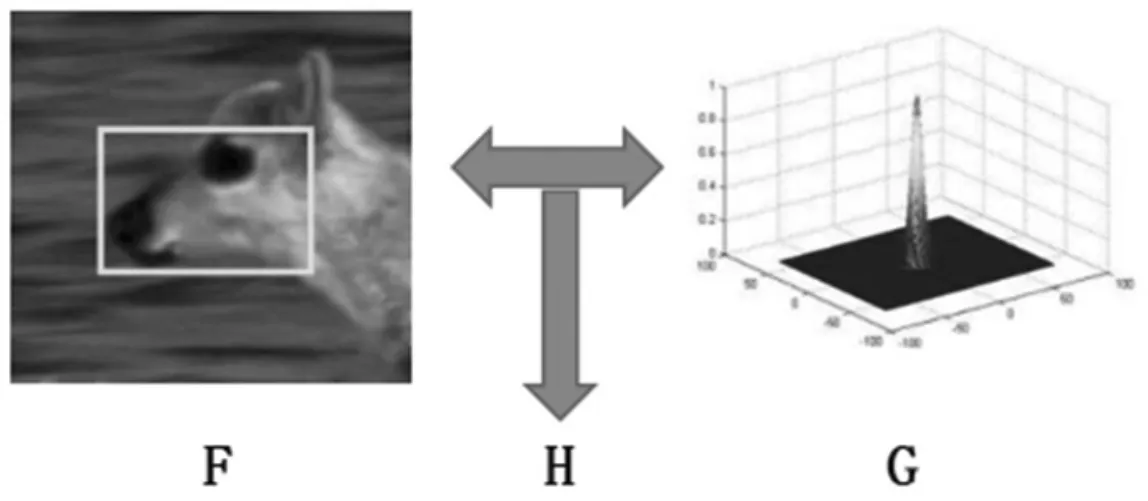
图2 相关滤波模型Fig.2 Correlation filtering model

Bolme 提出了一种使用误差最小平方和滤波器(MOSSE)的跟踪器，MOSSE 的思想[21]是,找到一个跟踪滤波器，使它在目标上的响应输出值最大，则公式如下

其中g、h、f 分别表示响应输出、滤波模板、输入的图像.上式的计算是进行卷积计算，计算耗时，因此对其采用快速傅里叶变换（FFT），把卷积计算变成点乘操作，能够极大减少计算量，从而将上式简变为

根据该式找到H

在实际跟踪过程中，为了提高滤波器模板的鲁棒性，以目标的m 个图像作为参考，从而提出模型公式如下

为了得到MOSSE 的最小值，将上式进行转换求导最后得到H 为

上式即滤波器的模型公式.

考虑滤波器的鲁棒性，对模板进行如下策略更新

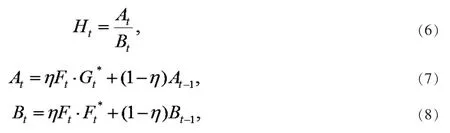
这里将模型公式更新分为分子At和分母Bt两个部分，η 表示学习率.

CF 通过 MOSSE 算法显示出巨大潜力，从此 CF 跟踪算法得到瞩目，大量基于 CF 的跟踪算法相继出现.Heriques 等利用训练块的循环结构，提出在具有HOG 特征的核空间[20]训练相关滤波器.Zhang 等[14]将上下文信息合并到过滤器学习中.SRDCF 跟踪器[24]通过对相关滤波系数进行空间位置惩罚来减轻边界效应[23]，通过减少样本的破坏来增强边界效应.

CF 的缺点是输入的特征为单通道灰度图像，特征表达能力有限；没有尺度更新，对于尺度变化的跟踪目标[24]不敏感.因此DCF 在多通道特征上做了优化.

1.2 判别相关滤波器

DCF 是Visual Tracking 领域应用最为广泛的跟踪算法.其核心思想是： 在目标跟踪过程中训练一个跟踪器，使用该跟踪器去检测预测的目标位置，然后再使用检测结果来更新训练集从而更新目标跟踪器.在训练目标跟踪器时采用HOG 特征[20]来描述感兴趣目标，选取的目标中心区域划分为正样本，目标周围区域划分为负样本.DCF 通过目标的循环移位构建训练样本，利用循环矩阵的特殊性，在离散傅里叶域进行求解，再借助于FFT 变换，将卷积变换[25]为频域的点乘，大大降低了计算的复杂度，提高了处理速度.

2 双HOG 特征的相关滤波器目标跟踪

针对环境变化对目标跟踪的影响，在HOG 特征基础上，本文提出基于双HOG 特征的相关滤波器目标跟踪方法，见图3.

图3 双HOG 特征相关滤波目标跟踪系统框图Fig.3 Block diagram of dual HOG feature correlation filtering target tracking system

2.1 HOG 特征

在计算机视觉以及图像处理中，方向梯度直方图是图像局部区域的梯度特征量统计，它的基本思想是采用梯度的统计信息来更好地描述目标的边缘信息，并通过局部梯度的大小对图像局部的外观和形状进行特征化.HOG 特征的提取过程为：首先为了减少光照以及背景等因素的影响，将颜色空间的对比度归一化；其次把图像划分成多个大小一样的单元，并计算各自相应的梯度直方图信息；然后把单元中所有特征串联起来，构成大的相互有重叠的块，然后统计整个块的直方图特征；为了进一步减少光照因素及噪声的影响，再对每个块内的梯度直方图进行归一化处理；最后将整个窗口中所有块的HOG 特征向量串联起来.

针对HOG 特征在目标跟踪中的特性， 提出以其作为进行目标位置估计的滤波器.由于HOG 是低级特性，为31 维度，所以不进行从粗到细的融合，只是简单地将它们连接起来构建DCF.为了获得更多特征，实验将补丁中所有像素的平均灰度值作为1 维特征，并将其与HOG 特征连接到一个32 维向量中，然后将其平均分解为两个16 维特征， 分别记为HOG1 和HOG2.HOG1 表示前面16 维特征，HOG2 表示后面16 维特征，两个特征线索各自进行相关滤波响应，最后选择响应值最大的特征进行目标位置的预测.

这里主要涉及线性回归问题，实质上是一种改良的最小二乘法.训练滤波器的目的是找到一个函数f（k）=wdk 使样本 xi及其回归目标 yi的平方误差最小

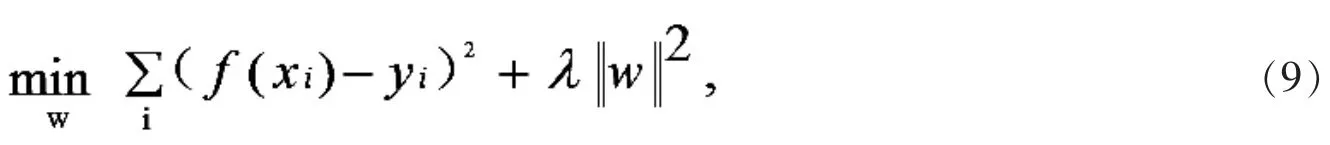
在傅里叶域中工作，其中的量通常是复数，推广到复数域，求得公式

根据循环矩阵在傅立叶空间可对角化的重要性质得到

其中，X 是循环矩阵，F 是离散傅里叶变换矩阵， X＾表示离散傅里叶变换.

对矩阵进行整合

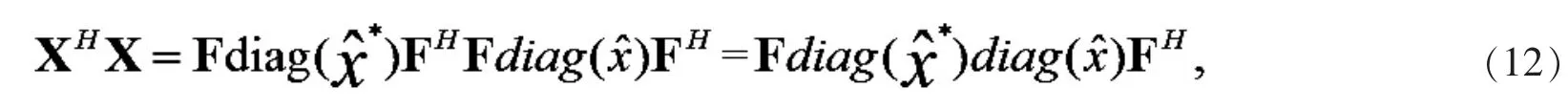
其中，*表示矩阵复共轭，根据点乘运算，上式可表示为

则所求线性回归的解的傅里叶变换可以表示为

因此，通过公式(15)计算具有相同大小x 的特征图矩形区域k 的响应值R，并搜索R 的最大值来识别新的目标位置

其中，d 表示特征维数，取值范围从1 到D.

2.2 算法

根据上述过程，双HOG 特征相关滤波算法DHCF 如下.

算法: 双HOG 特征相关滤波目标跟踪(DHCF)，

输入: 视频系列S1...Sn,以及第一帧的跟踪目标位置，

输出: 视频系列的跟踪目标位置P1...Pn.

1： 提取第一帧跟踪目标位置P1；

2： 初始化目标跟踪器；

循环直到视频结束:

3： 计算第t 帧的HOG 特征，并分割成HOG1 和HOG2，分别进行相关滤波处理；

4： 分别利用循环矩阵进行离散傅里叶变换，选择滤波处理的最佳结果；

5： 计算滤波处理好的特征响应图；

6： 在响应图中寻找最大值的位置，即预测出新的目标位置Pt+1.

返回视频系列的目标位置.

3 实验结果及分析

双HOG 特征目标跟踪方法在OTB-2013 和OTB-2015 两个基准上进行实验，其中OTB-2013 共有50个视频序列，OTB-2015 共有100 个视频序列， 将该跟踪器算法与六个跟踪器算法（Staple、SAMF、LCT、KCF、DSST、HOG）进行对比.

3.1 实验装置

实验环境为MATLAB R2018b，CPU 为i7 处理器，内存8G，64 位的Windows10 操作系统.实验按照标准DCF 方法[23]中的参数来构造HOG 特征，在OTB-2013、OTB-2015 两个基准数据集上进行测试评估.

3.2 参数设置

正则化参数λ 设置为0.01， 期望的相关输出标准差设置为位置滤波器的目标大小的1/16 和比例滤波器的1.5，过滤器大小M*N 设置为初始目标大小的两倍，学习率η 设置为0.025.将单元大小设置为1*1，用图像灰度特征增强HOG 特征，使用块大小为4*4 提取PCA_HOG 特征,将固定的补丁大小设置为初始目标大小.最后，提取的特征总是乘以一个Hann 余弦窗口.

3.3 实验结果

基于双HOG 特征的目标跟踪方法在精度和成功率上都提高了跟踪性能.图4、 图5 是在100 个序列运行后的成功率和精度图，从图中可看出DHCF 跟踪器在很多环境变化中性能优于其他跟踪器.

Staple、SAMF 和LCT 算法均以SRDCF 为基线，能够有效缓解边界效应，且优于标准DCF.DSST 采用了新颖的尺度算子，更好地融合了尺度特征.DHCF 算法只是以简单的DCF 为基准，上述算法和其他新技术也可以集成到该方法中，进一步提高性能.由于DHCF 算法为基于多特征的DCF 跟踪器提供了更好的替代方案，其他具有多种特征的跟踪算法也可以从该方法中受益.在图4 中，提出的DHCF 跟踪器在目标跟踪中取得了较好的性能，其成功率和精度在快速运动、背景混乱、形状变化等方面均优于其他算法，与传统HOG 算法相比也具有较优越的性能.图5 中，DHCF 跟踪器在跟踪成功率和精度方面总体性能都较好，其跟踪精度在面内旋转和光照变化方面不是最优的，分别为0.740 和0.732，都仅次于Staple 跟踪算法，分别为0.749和0.766， 分别相差0.009 和0.034.然而在低分辨率方面其跟踪精度取得了最佳为0.840，Staple 算法为 0.780， 传统HOG 算法为0.761， 比Staple 算法和传统HOG 算法分别高0.06 和 0.079.总体上看，DHCF 跟踪器显示的结果与其他跟踪器相比具有较好性能，并且在各种指标上均领先其他方法.

图4 各算法跟踪精度和成功率对比图Fig.4 Comparison chart of tracking accuracy and success rate of each algorithm

图5 各算法跟踪精度和成功率对比图Fig.5 Comparison chart of tracking accuracy and success rate of each algorithm

4 结论

本文提出了一种基于双HOG 特征的目标跟踪方法，充分展示了两个特征的优点.该方法中的两个特征通过不同的目标跟踪分析线索，选择最优的特征来确定跟踪结果.双HOG 特征在快速运动、背景杂乱等情况下有较好的鲁棒性，但在光照变化下性能相对较弱.实验表明，双HOG 特征目标跟踪算法在跟踪精度和效率上优于其他跟踪方法.下一步工作将结合颜色特征和HOG 特征做进一步研究.