当“发现”升级为“验证”
王庆菊
[摘 要]在学习“三角形的内角和”之前,很多学生都已经知道了“三角形的内角和是180°”这一结论,顺学而教,课堂教学的重心必然从“发现规律”升级为“验证结论”——让学生经历三角形的内角和之所以为180°的探究过程,让数学学习在建构中走向丰盈和深刻。
[关键词]理性思维;推理;深度建构;三角形的内角和
【教学内容】
人教版教材四年级下册第67页“三角形的内角和”。
【课前慎思】
1. 四年级学生大多数都知道“三角形的内角和是180°”这个结论,而且对此深信不疑,并没有太强的探究欲望。因此,即使教师让学生用量角器量或用剪拼角等方法验证这个结论,也是徒有形式的“虚假”操作。那么,本节课的生长点和核心是什么?
2.“内角”指“在封闭折线构成的图形内的夹角”。既然是研究三角形的内角和,“内角”自然成为绕不过的概念,而教材对于“内角”概念却只字未提。那么,需要专门进行“内角”概念教学吗?
3.用测量法、剪拼法、折拼法等研究三角形的内角和往往不能正好得到180°。对此,能否用“误差”一词以概之?
4. 数学之美在于理性思维,来不得一丝“差不多”。那么,是否有严密的适合学生验证“三角形的内角和”的方法,以帮助学生实现概念的深度建构?
【教学实践】
一、直观感知,认识内角、内角和
1. 初识内角、内角和
师(出示一个三角形,如右图):这是一个什么图形?

生(齐):三角形。
师:为什么叫三角形?
生1:因为它有三个角。
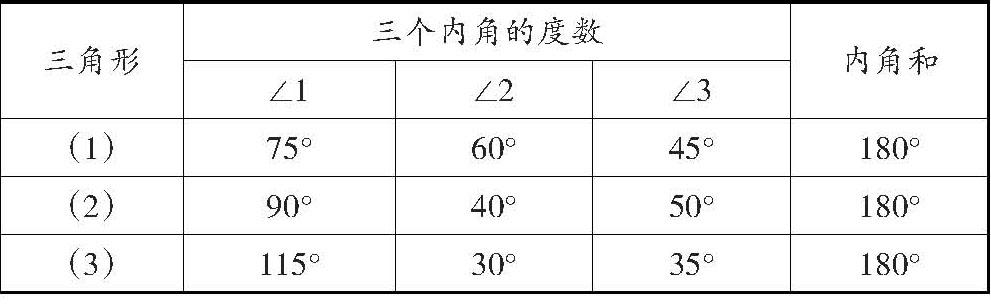
师:三角形的三个角∠1、∠2、∠3都在三角形的内部,我们可以叫它们什么角?
生2:内角。
师:把这三个内角的度数合起来,又叫什么?
生3:内角和。
2. 初识三角形的内角和

师:听说过三角形的内角和吗?谁能介绍自己了解到的有关三角形内角和的知识?
生4:三角形的内角和是180°。
师:你是怎么知道的?
生4:我是在书上看到的。
师:哪些同学真正研究过三角形的内角和?三角形的内角和真的是180°吗?
二、小组交流,实践验证
师:你准备用什么方法研究?请先想一想,然后在小组里交流,再选择合适的材料以小组为单位进行验证。小组合作要求:(1)利用学具袋中提供的(或自己设计的)材料,选择自己最喜欢的方法进行验证,并填好记录单。(2)通过验证,看看可以得出什么结论。

师:现在我们召开研究成果发布会。发言的小组选一名同学当主发言人,其他同学可以补充,下面的同学当小记者,随时准备提问。看哪个发言人表现最棒,哪个小记者最会提问题。
(1)度量法
生1:我们小组用的是测量的方法。先用量角器测量出三角形三个内角的度数,再算内角和,发现三角形的内角和正好是180°。其他同学有问题吗?
师:这的确是个好方法。其他小组测量的结果也是180°吗?好像有些同学遇到了一些问题。
生2:我们小组测量后发现,有的三角形的内角和是182°。
生3:我们小组测量的三角形的内角和是179°,也不是180°。
师:刚才大家都认为三角形的内角和是180°,但测量的结果有的是180°,有的不是180°。为什么会出现不同的结果?
生4:是不是量错了?
生5:可能量角器不准。
生6:可能没有把量角器放好。
師:的确,由于受测量工具或测量方法的影响,测量时只要有一点偏差,就会出现误差。数学需要严谨,还有别的方法吗?
(2)剪拼法
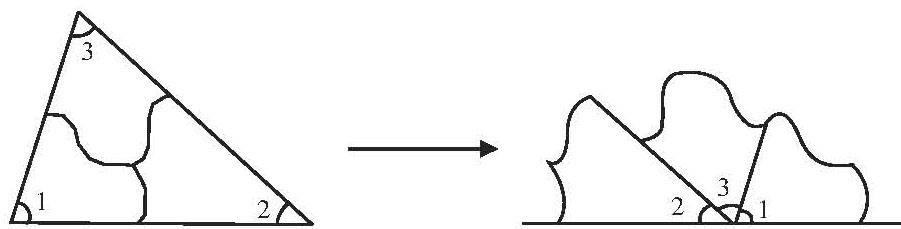
生7:我们小组用的是剪拼的方法。因为一个平角是180°,我们就想,如果三角形的三个内角刚好能拼成一个平角,不就能说明三角形的内角和是180°了吗?于是我们把三角形的三个角撕下来拼到一起,发现正好拼成一个平角,说明三角形的内角和是180°。
师:这个小组通过变换位置,把原本不在一起的三个角转化成一个平角。其他同学有问题要问吗?
生8:我觉得这种方法也不太准确——拼成的角和角之间也会有缝隙,不能确定正好是180°吧?
师:的确,这种方法也会产生一定的误差。刚才同学们分别用测量和剪拼的方法进行了检验,却发现三角形的三个内角的度数和未必正好是180°。
三、以疑促思,补充完善
师:学具袋里好像还有一个材料被大家忽略了。看看是哪个图形?
生1:长方形。
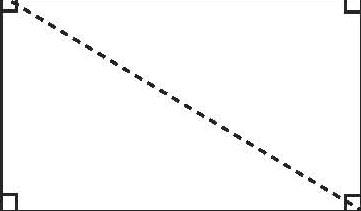
师:今天研究的是三角形的内角和。猜猜看,老师为什么要给大家准备这样一个长方形?
生1:这个长方形沿对角线剪开后可以得到两个完全一样的直角三角形。长方形的每个角都是90°,4个角一共360°,所以一个直角三角形的内角和就是180°。
师:这种方法好不好?好在哪里?
生2:好!这种方法避免了在剪拼过程中出现的误差。
生3:这种方法能说明直角三角形的内角和一定是180°。
师:是这样吗?这种方法实际上就是借助已知的准确数据——长方形的内角和是360°,推出直角三角形的内角和一定是180°。那么,现在可以说三角形的内角和是180°吗?
生4:不行。锐角三角形、钝角三角形的内角和还没有证明呢。
师:每个同学手中都有锐角三角形和钝角三角形,有没有办法进一步确认它们的内角和也是180°呢?
生5:是不是可以把锐角三角形、钝角三角形也转化成长方形或者直角三角形,从而得出它们的内角和?
师:试试看!
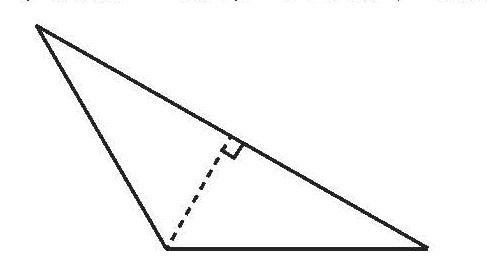
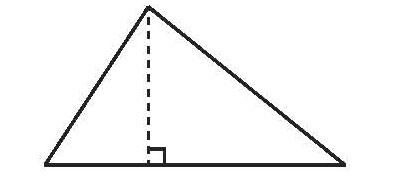
生6:在锐角三角形内画一条高,把它分成两个直角三角形,这两个直角三角形的内角和一共是360°,减去增加的两个直角的度数,那么,三角形的内角和是180°+180°-90°-90°=180°。
生7:在钝角三角形内画一条高,把它分成两个直角三角形,发现每个钝角三角形的内角和也是180°。
师:现在可以得出什么结论?
生8:所有三角形的内角和都是180°。
师:其实,早在300多年前,法国著名的数学家和物理学家帕斯卡就用这种方法验证了任何三角形的内角和都是180°,当时他只有12岁。(介绍帕斯卡的推理证明方法)
师:为什么三角形的形状不同,内角和却都是180°?这里面有没有什么奥秘?老师这里有一幅图(用几何画板演示不断变化的三角形),仔细观察,在这个过程中,什么变了?什么没变?你有什么发现?
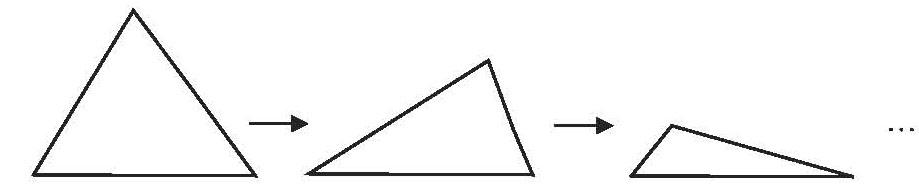
生9:三个角的度数都在变化,内角和却总是不变。
师:如果老师把上面这个角一直往下拉,猜一猜会出现什么情况?
生10:真神奇!这个角变成了一个180°的平角,另外两个角变成了0°,虽然这个图形已经不再是三角形,但这三个角的和仍然是180°。
师:不同的方法,同样的精彩!大家发现了吗?无论是撕一撕、折一折,还是拼一拼、分一分,这些方法都有异曲同工之妙,那就是都用了转化的策略。
四、应用感悟,丰富内涵
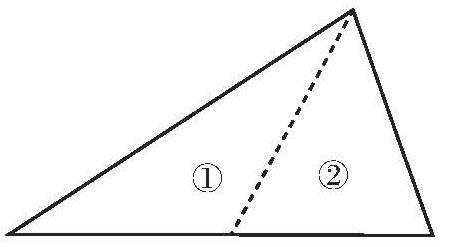
(1)一个三角形的内角和是180°,把这个三角形分成两个小三角形,这两个小三角形的内角和是180°吗?
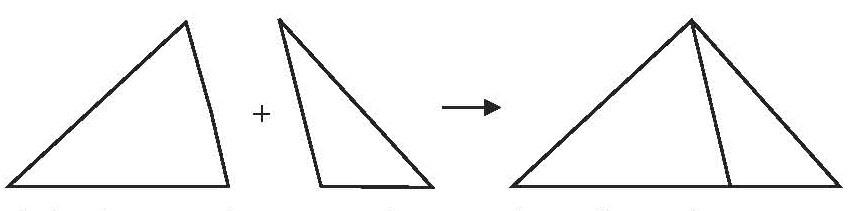
(2)把两个三角形拼成一个大三角形,拼成的大三角形内角和是180°吗?
(3)著名数学家陈省身爷爷在北京大学的一次讲学中语惊四座:“人们常说,三角形内角和等于180°。但是,这是不对的!”这又是为什么呢?
【课后思考】
1.重要的是验证结论
虽然很多学生在课前就知道“三角形的内角和是180°”,但对他们而言,这仅仅是一个听来的信息而已。三角形的内角和为什么是180°,学生未必思考过。因此,本节课的教学重点不仅仅在于“三角形的内角和是多少度”,更重要的是“用什么方法来说明三角形的内角和是180°”,即让学生通过量、撕、拼、折等方法,经历“三角形的内角和为180°”的探究过程。正如毕达哥拉斯所言:在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。
2.在质疑中走向深刻
关于三角形的内角和,测量也好,剪拼、折拼也罢,误差是不可避免的,许多教师对此不以为然,直接告诉学生这是误差惹的祸。但是,用“误差”之说解释“三角形的内角和是180°”,是不是同样可以解释“三角形的内角和是179°” “三角形的内角和是182°”?如此,为什么三角形的内角和偏偏是180°?
本节课之初,当教师让学生想办法证明三角形的内角和是180°时,很多学生想到的就是用量角器测量三个角的度数。但测量的结果并未如他们所听所想的那样正好是180°。于是,有的学生开始想办法“解决”这个问题:或调整测量结果,“凑”出180°;或先测出其中两个角的度数,再用180°减去这两个角的度数求出第三个角的度数,以迎合“三角形的内角和是180°”。对此,如果仅以“误差”一词以概之,势必会影响学生严谨的科学作风和实事求是的科学精神的形成。
本节课中,从学生对“三角形的内角和是180°的深信不疑,到测量法、剪拼法的不精确,使学生对“三角形的内角和是180°”将信将疑,再到借助长方形论证以及几何画板演示使学生对 “三角形的内角和一定是180°”确信无疑,學生经历了一个完整的探究发现过程,提升了思维品质,让数学学习在质疑中走向深刻。
3.在推理中触摸理性
中科院院士姜伯驹认为,“不讲证明,数学课就失去了灵魂。其实,数学上很多概念并不是完全可以实验出来的。比如三角形的内角相加是180°,你真用尺子去量,可能会有误差,也许就得不到这个180°。” 数学之美在于理性思维,推理是数学思维的核心。
本节课中,当测量、剪拼等方法均不能很好地解释三角形的内角和为什么是180°时,借助学生熟知的、显而易见的“长方形的四个内角都是90°”“长方形的内角和是360°”这一经验性数学事实,再结合长方形与直角三角形的内角关系,从特殊到一般进行推理,使学生真正理解了三角形的内角和之所以是180°的数学本质,同时感受转化、变与不变的数学思想和推理力量,有效消除了直观感知的尴尬,课堂在丰富和深刻中绽放出理性的光辉和散发出浓浓的数学味。
(责编 金 铃)

