深度学习：让学习真正发生

王庆菊

[摘 要]深度学习是对工具性学习和浅表学习的超越。探寻小学数学深度学习的内涵及特征，架构促进深度学习的基本路径，从而推动数学学习的真正发生。

[关键词]深度学习;内涵;特征;课堂基本样态;教学策略

2016年9月13日，《中国学生发展核心素养》刚发布，就成为教育教学改革的行动纲领和终极目标。

核心素养落地，主渠道在课堂。反观当下的小学数学教育，大多停留在刻板化、流程化、碎片化等浅表学习和表演学习的层面，在中小学数学课堂上，深度学习的缺失已是不争的事实：过度强调学习的间接经验性、知识的客观真理性、教学的直接传递性，心中有案，行中无人;务探究之虚，行灌输之实，将富有挑战性的探究过程简化为庸俗化互动、程序式合作、按图索骥式操作;忽视文本内隐的丰富内涵，只有数学形式的呈现……于是，学生学得粗浅且未触及数学本质，学得懵懂且缺少理性思考，学得囫囵吞枣且食而不化，学得虚假且滥竽充数，学得艰涩且乏味生厌。这样的学习消解了数学学习的本真教育涵养，不仅没深度，而且使得数学学习从未真正发生，是虚假学习。何谈核心素养培养？

汪宇先生说：“我们对数学的理解悖逆数学的本质到了多么严重的程度。功利实用倾向和计算技能崇拜遮蔽了数学的本质精神。因此，国民的科学精神和基本思维能力依然令人失望。”究其原因，一是绝对主义的数学观根深蒂固，把数学看成绝对真理的集合，缺乏向数学学科本质的回归;二是数学教师本体性知识不足，不能从本源上把握数学知识的本质、内在联系及蕴含的思想方法，使深度学习沦为空谈。

教师唯书为经，不求甚解，以其昏昏如何使学生昭昭？何谈学生之思之究？在“百度一下你就知道”的时代，我们必须从“教学即传递”的观念中走出来，关注知识的多维价值，着眼知识的深层次理解和深度处理，让教与学走向深入、走向深刻、走向深度，由此达成培养学生核心素養的高层次发展目标。

一、小学数学深度学习的内涵

整合性学习。深度学习是基于问题的多维知识整合，强调将新概念与已知概念和原理联系起来，在各种观点之间建立多元连接，实现对知识的整体感知与学习。

意义性学习。深度学习是基于建构主义理论的一种学习方式，着重引导学生通过与文本、教师、环境等多因素的对话以及对于学习对象的“前理解”的不断修正，形成深切体验和深入思考，“知其然又知其所以然”，达成对学科本质和知识意义的自我理解，完成深层次的学习和内在品质的提升。

批判性学习。笛卡尔说：“我唯一不怀疑的是我的怀疑精神。”深度学习是一种注重对知识进行批判性理解的学习，强调学习者对其中的某些观点、做法保持批判或质疑的态度，对学习进行反思，以充分的理性进行审视、分析、鉴别、评价，探明真伪，并在必要时探索调整或改造的途径，提出新观点和新方法。

阶梯式学习。深度学习触及事物的本质并向更高阶段发展，其过程必然是由浅入深、由表及里、由外到内逐层建构的。与此相对应，学生的深度学习是促进式、层次性、阶梯式地逐步探及兴趣、情感和思维的深处。

因此，就小学数学而言，深度学习是在教师引领下，学生围绕具有挑战性的学习主题，全身心参与、体验成功、获得发展的过程。在这个过程中，学生超越表层的符号学习而进入知识的“深处”，理解学习过程，把握学科本质和思想方法，促进元认知能力、问题解决能力、批判性思维、创造性思维等高阶能力的发展，并由理性思维走向理性精神。

二、小学数学深度学习的特征

相对于浅表学习，深度学习的特征主要体现在以下方面：

主动与卷入。学生对学习充满兴趣，在情境、问题或学习任务的驱动下“卷入”学习，积极主动地投入学习过程，通过与环境、他人和文化的反思性相互作用形成自我感，并能互相评价、追问、质疑、补充、纠错等。

理解与批判。学生围绕学习内容深入思考、对话，积极表达与展示自己的思维过程，在质疑与辨析中加深对深层知识和复杂概念的理解。

联系与建构。学生运用原有的知识经验对新概念（原理）或问题进行分析、鉴别、评价，将新概念与已知概念和原理联系起来，主动地对新知识做出理解判断、审视反思，形成对知识的理解，建构新知序列。

迁移与应用。学生对学习情境深入理解，对关键要素准确判断和把握，在相似情境中能够做到触类旁通、举一反三，创造性地解决问题。

三、基于深度学习的课堂基本样态

1.问题引领

“问题引领”就是以问题为核心，以问题为载体，将学生的思维引向深处。正如吴正宪老师所言：我们应当让思维在“问题链”中“浅入深出”。“问题引领”课堂样态的基本结构如下：

在这些环节中，“创设情境”是前提，“生成问题”是核心，“互动释疑”是关键，“建构知识”是重点，“总结反思”是提升。

【案例】轴对称

首先，通过“折一折、剪一剪”游戏，激发学生兴趣，以“对折”的动作，帮助学生初步感知轴对称图形。

接着，设计三个核心问题组成“问题串”，层层深入地引领学生探索理解“轴对称”。

（1）怎样判断一个图形是不是轴对称图形？（以长方形、正方形、三角形、平行四边形为例）

（2）只折一次，就说一个图形是或不是轴对称图形，行不行？

（3）第一次对折就已经完全重合了，为什么还要再对折呢？我们在研究什么？

这样，借助“对折”，带学生“玩”对称、“识”对称、“做”对称、“赏”对称，深入知识层面、方法层面、思想层面，可使学生“知其所以然”，培养学生发现问题、分析问题和解决问题的能力，促进学生对规律的理解。

2.体系建构

“体系建构”是指以数学知识系统和学生认知系统为基础，分析某个知识点在知识系统中的地位，把知识点纳入知识系统中，以系统的、整体的教学观展开教学，帮助学生在理解知识的同时，把握整体与局部、本质与现象的关系，以结构来统领知识。“体系建构”课堂样态的基本结构如下：

【案例】多边形的面积

在按照教材的编排顺序教学了平行四边形的面积、三角形的面积和梯形的面积后，教师提出问题：

（1）你能只用一个公式就表示出平行四边形、三角形、梯形面积的计算方法吗？

（2）教材按照“先平行四边形，再三角形，最后梯形”的顺序来研究三个图形的面积计算方法，可以调整学习的顺序吗？为什么？

（3）为什么教材依然按“先平行四边形，再三角形，最后梯形”的顺序来研究？

对教材内容进行系统还原，把学生“卷入”项目学习中，不断进行意义的建构，既沟通了知识之间的联系，启发学生把问题想深想透，又培养了学生追问和反思的习惯和能力。

3.追根溯源

深度学习鼓励追根溯源，刨根问底，凸显对数学本质的感悟、理解和掌握。以追根溯源为线索开展教学，使学生在逐层探究中经历数学知识的再创造活动，真正感知和领悟数学特有的价值与魅力。“追根溯源”课堂样态的基本结构如下：

【案例】2的倍数

（1）举例研究

[①]写出几个2的倍数，观察它们有什么特点。

[②]猜想：个位上是0、2、4、6、8的数，都是2的倍数。

[③]质疑： 2的倍数的个位上的数字必须是0、2、4、6、8吗？

[④]反例：说出个位上不是0、2、4、6、8的数，看看这些数是不是2的倍数。

（2）本质探究

[①]质疑：判断一个数是不是2的倍数，为什么只看个位上的数字而不看其他数位上的数字？

[②]猜想：既然这样，能结合数的组成去寻求内在原因吗？比如，把一个数拆分成由各个数位上的数组成的数，如356=300+50+6。你有什么发现？

[③]探究：2的倍数与拆分后的算式中的哪些数有关？与哪些数无关？

[④]讨论：判断一个数是不是2的倍数，为什么只看这个数的个位上的数字？

4.质疑批判

深度学习要求学习者对学习材料保持批判或怀疑的态度，并从多个角度来进行批判性的分析，进而解决疑问、修正观念，加深对深层知识和复杂概念的理解。“质疑批判”课堂样态的基本结构如下：

【案例】圆锥的体积

当用倒水等方法得出等底等高的圆柱体积是圆锥体积的3倍后，有学生提出以下疑问：

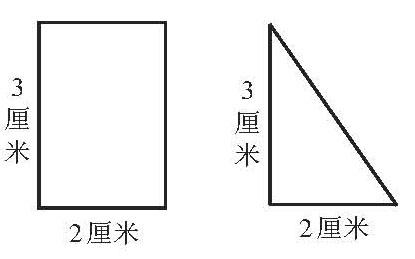
（1）如图，将长方形、直角三角形都以3厘米的边为轴旋转一周，分别可以得到圆柱和圓锥。既然长方形的面积是等底等高的三角形面积的两倍，那么圆柱体积是不是应该是等底等高的圆锥体积的2倍？圆柱与圆锥的体积为何变成了3倍关系？

（2）通过倒水实验，我们看到圆柱体积是等底等高的圆锥体积的3倍。这个数值准确吗？有可能是2倍多一点或者是3.14倍吗？

是不是眼睛欺骗了我们？事实和理论什么地方不一致？学生的质疑合乎情理。若以问题引领持续研究，这种深度探究的背后必将是学生思维由表层走向深入，由草率迈向成熟。

四、促进深度学习的教学策略

1.深度设计

深度学习的一个重要标志，就是能将外在的教学内容转化为学生内在的精神力量，而教学内容并不能直接转化为学生的精神力量，必先转化为学生能够进行思维操作和加工的学习素材。因此，深度设计是深度学习的前提，这就需要教师全面分析教材、深度挖掘教材、灵活整合教材，从微观上准确、深刻地理解数学知识，寻找和提炼核心内容以及关键问题。

【案例】教学“体积和体积单位”时，为了让学生充分经历知识的形成过程，可以设置探究主题：

（1）所有的物体都有体积。

（2）体积的大小可以用数值来表示。

（3）测量体积需要有统一的体积单位。

（4）任何一个物体的大小，都可以通过与体积单位的比较而确定数值。

这样，学生不仅能正确把握数学知识的整体结构，更能领悟知识背后隐含的思想方法。

2.深度探究

苏霍姆林斯基说：“教育，首先是活生生的、寻根问底的、探究性的思考。”有思考才有深度，有深度必须要思考。因此，要从高观点“居高临下”地认识小学数学，在问题引导下，引导学生独立思考、自主判断、层层推理，由浅入深、由表及里、多层次地对知识进行考察分析与思考，从而揭示知识的本质，拓展学科视野，进而从事理到哲理，发现新问题，提出新观点，探寻新规律。

【案例】教学“找次品”时，可以设计以下问题串，引领学生思考：

（1）是不是只要把待测物品分成3份，称的次数就最少？

（2）为什么把待测物品平均分成3份，称的次数最少？

（3）对于不能平均分成3份的待测物品，为什么数量要尽可能接近？

3.深度反思

孔子云：“吾日三省吾身”，“学而不思则罔，思而不学则殆。”反思是认识过程中强化自我意识、进行自我监控与自我调节的重要形式，乐于反思、善于反思，能够使学生成为自觉、自律、自主的学习者，使所学知识更加深刻、更加系统化。

【案例】 “体积和体积单位”的结课阶段，可引导学生思考：今天这节课上，我们在长度和长度单位、面积和面积单位的基础上，研究了体积和体积单位。它们有什么不同？有没有什么相同之处？

这样的反思活动，从一维到二维，再到三维，唤醒了学生的度量经验，沟通和深化了学生对度量本质的把握。至此，体积和体积单位与之前的其他度量单位具有内在的一致性，能有机融入学生原有的认知背景中，使学生获得新的生长。

撑一支长篙，向意义更深处漫溯。深度学习提升了学生学习的境界，丰富了学生学习的层次，让学习真正发生。相信，我们一定会满载一船星辉，和学生一起歌唱。

（责编 金 铃）